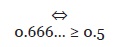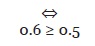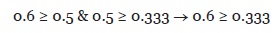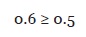Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação
versão impressa ISSN 1646-9895
RISTI no.34 Porto out. 2019
https://doi.org/10.17013/risti.34.97-111
ARTÍCULOS
Métricas para la Medición del Factor de Flexibilidad y el Factor de Herencia de Implementación de Sistemas de Software
Metrics for the Measurement of the Flexibility Factor and the Inheritance Implementation Factor of Software Systems
Orlando Ortiz-Gutierrez1, René Santaolaya-Salgado1, Olivia-Graciela Fragoso-Díaz1, Juan-Carlos Rojas-Pérez1
1Tecnológico Nacional de México/CENIDET, Depto. Ciencias Computacionales, Interior Internado Palmira S/N, Col. Palmira, C.P. 62490, Cuernavaca, Morelos, México. orlando.ortiz18ce@cenidet.edu.mx, rene@cenidet.edu.mx, ofragoso@cenidet.edu.mx, carlos.rojas@cenidet.edu.mx
RESUMEN
Actualmente la medición de la calidad del diseño arquitectural de software es un tópico importante para los ingenieros de software. Sin embargo, algunas métricas de calidad aún no están definidas, como lo son las métricas para medir el factor de flexibilidad y de herencia de implementación de una arquitectura de clases, enfocadas en métodos abstractos. En este trabajo de investigación se propone un conjunto de cinco métricas de calidad, tres de ellas son para medir el factor de herencia de implementación, las cuales son: Factor de Herencia de Implementación (FHI), Factor de Herencia de Implementación por Jerarquía de Clases (FHIJ) y Factor Herencia de Implementación de una Arquitectura de Clases (FHIAC); las dos restantes son para medir el factor de flexibilidad, estas son: Factor de Flexibilidad de Clase (FFC) y Factor Medio de Flexibilidad de Clases(FMFC).
Palabras-clave: Acoplamiento; flexibilidad; herencia de interfaz; herencia de implementación.
ABSTRACT
Currently measuring the quality of architectural software design is an important topic for software engineers. However, some quality metrics are not yet defined such as the metrics for measuring the flexibility and implementation inheritance factor for a class architecture focused on abstract methods. In this research, a set of five quality metrics is proposed; three of them are to measure the inheritance implementation factor, which are: Implementation Inheritance Factor (FHI), Implementation Inheritance Factor by Class Hierarchy (FHIJ) and Implementation Inheritance Factor of a Class Architecture (FHIAC); the remaining two are to measure the flexibility factor, these are: Class Flexibility Factor (FFC) and Average Class Flexibility Factor (FMFC).
Keywords: Coupling; flexibility; interface inheritance; implementation inheritance.
1. Introducción
Actualmente la medición de la calidad del diseño arquitectural de software es un tópico importante para los ingenieros de software. Sin embargo, algunas métricas de calidad aún no están definidas, como lo son las métricas para medir el factor de flexibilidad y de herencia de implementación de una arquitectura de clases. Entendiéndose por flexibilidad, como la facilidad con la que un sistema o componente puede modificarse para su uso en aplicaciones o entornos distintos de aquellos para los que fue específicamente diseñado (IEEE Standard Glossary of Software Engineering Terminology, 1990) y por herencia de implementación, una relación donde una subclase hereda la implementación del comportamiento de su clase base (Pinto, 2015). Esta carencia reprime la identificación de código desagradable (del Inglés smell code), en el software legado, que impacta en anti patrones de diseño e impide su mejora por medio de técnicas de refactorización y de reingeniería.
Para efectos de reducir el acoplamiento entre clases relacionadas por herencia de implementación en arquitecturas orientadas a objetos se necesita, una métrica que mida el acoplamiento por herencia de implementación y otra métrica para medir la flexibilidad, de un diseño arquitectural de software.
Se han revisado diferentes trabajos de investigación sobre métricas para medir algunos atributos de calidad, como lo son: acoplamiento, reusabilidad, flexibilidad, comprensibilidad, funcionalidad, extensibilidad y efectividad. Sin embargo, en la literatura revisada no se han encontrado métricas cuyo propósito sea medir el factor de flexibilidad y de herencia de implementación desde métodos abstractos, por ejemplo: en (Chawla & Nath, 2013) se mide la herencia y el acoplamiento a nivel de clase y de sistema, pero ninguna de las métricas toman en cuenta métodos abstractos; en (Chawla & Chhabra, 2013) se mide la flexibilidad utilizando una fórmula que utiliza los atributos de encapsulación, acoplamiento, composición y polimorfismo pero tampoco ninguna de las métricas utilizadas toman en cuenta los métodos abstractos. Consecuentemente, en esta investigación se definió un conjunto de métricas para la medición de la flexibilidad y el acoplamiento por herencia de implementación desde clases abstractas, utilizando la teoría de la medición para sustentarlas.
2. Marco Teórico
Recientemente se ha sugerido que la teoría de la medición debería servir de base para desarrollar, razonar y aplicar métricas de ingeniería de software (Briand, El Emam, & Morasca, 1996).
Para clasificar una métrica como de escala ordinal, se deben cumplir los requisitos del axioma de orden débil, los cuales son: que "≥ sea una relación binaria total y transitiva. Las propiedades de transitividad y completitud, son las siguientes (Suze, 1995):
3. Materiales y Métodos
3.1. Escalas o Niveles de Medición
Una asociación que se establece entre el mundo real y valores de medida, se suele denominar escala de medición. La teoría de la medición permite formalizar la relación entre dos escalas de medición con esta definición (Gary, 2010):
Sea (A, B, μ) una escala, donde el conjunto de objetos en B, es el conjunto de los números reales. Sea que la notación μ(A) significa que el conjunto de todos los números reales que son mediciones de algún objeto en A. Esto es que μ(A) es el conjunto de medidas de los objetos en A. (En matemáticas, a esto se la llama el rango de μ). Luego un mapeo t: μ(A) .-> B se define como una transformación admisible, si y sólo si, (A, B, t°μ) también es una escala.
Se pueden describir cinco tipos de escalas que se caracterizan por sus transformaciones admisibles (Gary, 2010): nominal, ordinal, de intervalo, de proporción (ratio) y absoluta.
Específicamente, las escalas ordinales asignan números a objetos en un orden particular, pero cualquier número que mantiene el orden es igualmente bueno. Cualquier función estrictamente creciente de t, es una transformación admisible. Un ejemplo es la escala de Mohs para la dureza de los minerales. La escala original asigna, por ejemplo, 1 al talco, 7 al cuarzo y 10 al diamante. Años después, se creó una escala que asignó 1 al talco, 8 al cuarzo y 15 al diamante. Los números difieren, pero el orden sigue siendo el mismo. En este caso se cumple que aun cuando se transforme la escala no cambia el orden creciente, por lo tanto, es una transformación admisible (Gary, 2010). Esta es la escala en la que se definen las métricas propuestas, puesto que cumplen con los axiomas de la teoría de la medición para pertenecer a esta escala.
3.2. Factor de Herencia de Implementación (FHI) como escala ordinal
Se tiene el siguiente sistema relacional empírico:
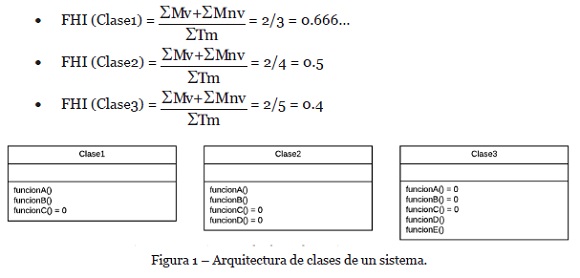
Como parte del proceso de comprobación de las condiciones anteriores, se utiliza la ecuación (1) de la sección 4.1 para realizar el cálculo del FHI de las clases uno, dos y tres, ubicadas en la Figura 1. En donde los métodos que tienen “= 0”, significa que son abstractos, y los que no lo tienen, quiere decir que tienen una implementación en su cuerpo. Obteniéndose los siguientes resultados de la Figura 1:
Para comprobar que la relación binaria es de orden débil, tiene que cumplir con las propiedades de transitividad y completitud.
Transitividad
Como se puede observar, la clase1 tiene un factor de herencia de implementación mayor al de la clase2. Este a su vez tiene un factor de herencia de implementación mayor al de la clase3. Concluyendo que la relación binaria •≥ cumple con la propiedad de transitividad.
Relación Total
Si se tienen las clases uno y dos, se debe poder decir que la clase 1 “tiene mayor o igual factor de herencia de implementación que” la clase 2, o viceversa. Es decir:
Clase1 •≥ Clase2 o Clase2 •≥ Clase1
Calculando el FHI en las clases uno y dos de la Figura 1, siempre fue posible determinar cuando existía mayor o igual factor de herencia de implementación.
Homomorfismo
Comprobando la segunda condición quedaría de la siguiente manera:
La clase 1 “tiene mayor o igual factor de herencia de implementación que” la clase 2
Conclusión
La relación binaria “tiene mayor o igual factor de herencia de implementación que” de la métrica FHI, cumple con las condiciones de orden débil y además es un homomorfismo. Por lo cual, se concluye que la métrica es de escala ordinal (Suze, 1992).
Bajo el mismo sustento de la teoría de la medición se diseñaron las métricas para el Factor de Herencia de Implementación por Jerarquía de Clases (FHIJ) como Escala Ordinal y Factor de Herencia de Implementación de una Arquitectura de Clases (FHIAC) como escala ordinal.
3.3. Factor de Herencia de Implementación por Jerarquía de Clases (FHIJ) como Escala Ordinal
Bajo el mismo sustento de la teoría de la medición se diseñó la métrica para el Factor de Herencia de Implementación por Jerarquía de Clases (FHIJ) como Escala Ordinal. Obteniéndose los siguientes resultados al aplicar la ecuación (2)
Conclusión
La relación binaria “tiene mayor o igual factor de herencia de implementación que” de la métrica FHIJ, cumple con las condiciones de orden débil y además es un homomorfismo. Por lo cual, se concluye que esta métrica es de escala ordinal (Suze, 1992).
3.4 Factor de Herencia de Implementación de una Arquitectura de Clases (FHIAC) como escala ordinal
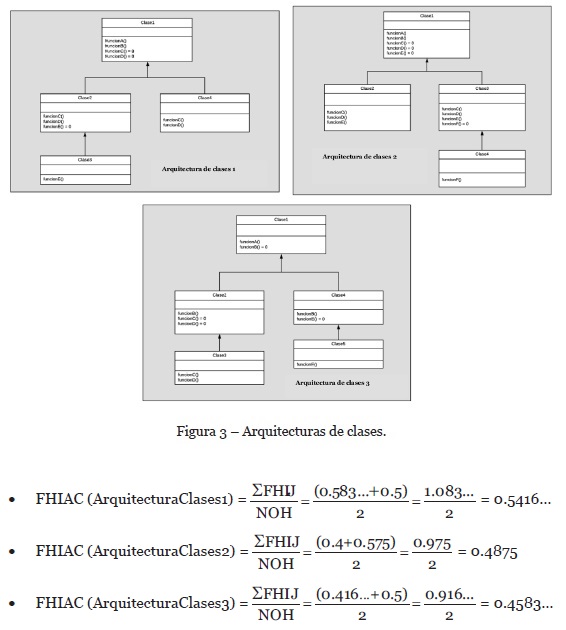
Así mismo, se diseñó la métrica para el Factor de Herencia de Implementación de una Arquitectura de Clases (FHIAC) como escala ordinal. Obteniéndose los siguientes resultados al aplicar la ecuación (3) de la sección 4.3, a las arquitecturas de clases mostradas en la Figura 3:
Conclusión
La relación binaria “tiene mayor o igual factor de herencia de implementación que” de la métrica FHIAC, cumple con las condiciones de orden débil y además es un homomorfismo. Por lo cual, se concluye que la métrica es de escala ordinal (Suze, 1992).
3.5. Factor de Flexibilidad de Clases (FFC) como escala ordinal
Para las métricas de flexibilidad se tiene el siguiente sistema relacional empírico:
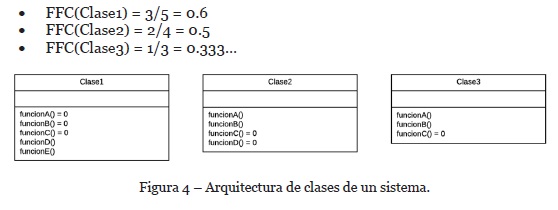
Como parte del proceso de comprobación de las condiciones anteriores, se utiliza la ecuación (4) de la sección 4.4 para realizar el cálculo del FFC de las clases uno, dos y tres, ubicadas en la Figura 4. En donde los métodos que tienen “= 0”, significa que son abstractos, y los que no lo tienen, quiere decir que tienen una implementación en su cuerpo. Obteniéndose los siguientes resultados de la Figura 4:
Para comprobar que la relación binaria es de orden débil, tiene que cumplir con las propiedades de transitividad y completitud.
Transitividad
Como se puede observar, la clase 1 tiene un factor de flexibilidad de clase mayor al de la clase 2. Éste a su vez tiene un factor de flexibilidad mayor al de la clase 3, debido a la cantidad de métodos virtuales (con comportamiento polimórfico) que tienen. Concluyendo que la relación binaria •≥, cumple con la propiedad de transitividad.
Relación Total
Si se tienen las clases uno y dos, se debe poder decir que la clase 1 “tiene mayor o igual factor de flexibilidad de clase que” la clase 2, o viceversa. Es decir:
Clase1 •≥ Clase2 o Clase2 •≥ Clase1
Calculando el FFC en las clases uno y dos de la Figura 4 siempre fue posible determinar cuando existía mayor o igual factor de flexibilidad.
Homomorfismo
Comprobando la segunda condición quedaría de la siguiente manera:
La clase 1 “tiene mayor o igual factor de flexibilidad que” la clase 2
Demostración empírica de la propiedad de transitividad
Demostración formal de la propiedad de transitividad
Reflejado en números, se tiene que:
Como se puede observar, la clase 1 tiene un factor de flexibilidad de clase mayor al de la clase 2. Éste a su vez tiene un factor de flexibilidad mayor al de la clase 3, debido a la cantidad de métodos virtuales con comportamiento polimórfico que tienen. Concluyendo que la relación binaria •≥, cumple con la propiedad de transitividad.
Demostración empírica de la propiedad de completitud
Si se tienen las clases uno y dos, se debe poder decir que la clase 1 “tiene mayor o igual factor de flexibilidad de clase que” la clase 2, o viceversa. Es decir:
Clase1 •≥ Clase2 o Clase2 •≥ Clase1
Demostración formal de la propiedad de completitud
Calculando el FFC en las clases uno y dos de la Figura 4 siempre fue posible determinar cuando existía mayor o igual factor de flexibilidad.
Demostración empírica de FFC que es un homomorfismo
Comprobando la segunda condición quedaría de la siguiente manera:
La clase 1 “tiene mayor o igual factor de flexibilidad que” la clase 2
Formalmente
Conclusión
La relación binaria “tiene mayor o igual factor de flexibilidad que” de la métrica FFC, cumple con las condiciones de orden débil y además es un homomorfismo. Por lo cual, se concluye que la métrica es de escala ordinal (Suze, 1992).
3.6.Factor Medio de Flexibilidad de Arquitecturas de Clases (FMFAC) como escala ordinal
Bajo el mismo sustento de la teoría de la medición se diseñó la métrica para Factor Medio de Flexibilidad de Arquitecturas de Clases (FMFAC) como escala ordinal.
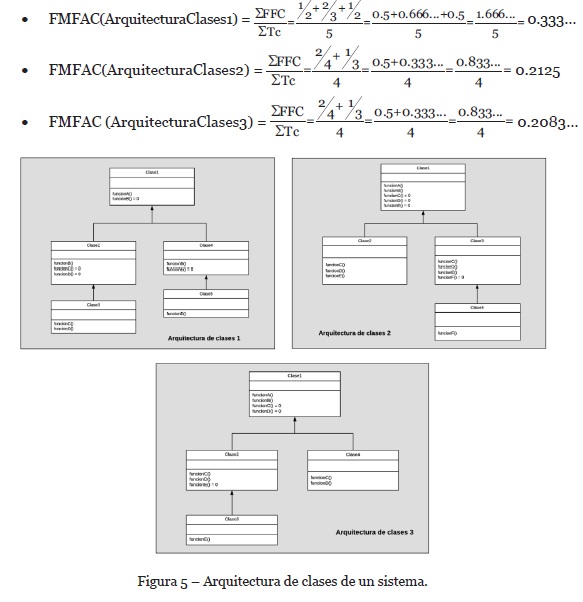
Obteniéndose los siguientes resultados al aplicar la ecuación (5) de la sección 4.5, a las arquitecturas de clase mostradas en la Figura 5:
Conclusión
La relación binaria “tiene mayor o igual factor medio de flexibilidad de la arquitectura de clases” de la métrica FMFAC, cumple con las condiciones de orden débil y además es un homomorfismo. Por lo cual, se concluye que la métrica es de escala ordinal (Suze, 1992).
4. Resultados
Se obtuvo un conjunto de métricas para medir el factor de flexibilidad (FFC y FMFAC) y de herencia de implementación (FHI, FHIJ y FHIAC), en diseños arquitecturales de clases, descritas más a detalle a continuación:
4.1. Métrica FHI (Factor de Herencia de Implementación)
Se ha definido una métrica para medir el factor de herencia de implementación que tiene una clase con respecto a otra. Dada una clase derivada, esta métrica consiste en la suma de los métodos virtuales y no virtuales implementados en su clase base, entre el número total de métodos de dicha clase base.
La expresión matemática de la métrica FHI se muestra a continuación:
En donde:
ΣMv = Sumatoria de métodos virtuales implementados en una clase base.
ΣMnv = Sumatoria de métodos no virtuales implementados en una clase base. Tm = Total de métodos en una clase base.
Debido a la normalización de la métrica, los valores obtenidos no dependen de la cantidad de métodos que se tengan en una clase dada. El valor óptimo es 0, lo cual significa que no se está heredando la implementación de los métodos. En caso contrario, el valor menos deseado es el 1, lo que significa que todos sus métodos están heredando su implementación.
4.2.Métrica FHIJ (Factor de Herencia de Implementación de una Jerarquía de Clases)
Se ha definido una métrica para medir el factor de herencia de implementación que tiene una jerarquía de clases. Esta métrica consiste en que, para una jerarquía de clases dada, es la suma del FHI de cada subclase entre el número total de clases en esa jerarquía menos 1.
La expresión matemática de la métrica FHIJ se muestra a continuación:
En donde:
ΣFHI = Sumatoria de FHI de una clase base.
Tc = Total de clases en esa jerarquía.
De la misma manera, el valor óptimo es 0, lo cual significa que no se está heredando la implementación de los métodos en la jerarquía, y 1 es el valor menos deseado, lo que significa que todos sus métodos están heredando su implementación.
4.3.Métrica FHIAC (Factor de Herencia de Implementación de una Arquitectura de Clases)
Se ha definido una métrica para medir el factor de herencia de implementación que tiene una arquitectura de clases. Esta métrica consiste en la suma de los FHIJ de las ramas de clases entre el número de jerarquías de clases (NOH). La expresión matemática de la métrica FHIAC se muestra a continuación:
En donde:
ΣFHIJ= Sumatoria de FHIJ de una jerarquía de clases.
NOH = Es el conteo de las jerarquías de clase.
De la misma manera, el valor optimo es 0, lo cual significa que no se está heredando la implementación de los métodos en una arquitectura de clases, y 1 es el valor menos deseado, lo que significa que todos sus métodos están heredando su implementación.
4.4. Métrica FFC (Factor de Flexibilidad de Clases)
Se ha definido una métrica para medir el factor de flexibilidad que tiene una clase con respecto a otra. Dada una clase base, esta métrica consiste en la suma del NOP, entre el número total de sus métodos. La expresión matemática de la métrica FFC se muestra a continuación:
En donde:
ΣNOP = Sumatoria de los métodos virtuales que exhiben un comportamiento polimórfico.
Tm = Total de métodos en una clase base.
Debido a la normalización de la métrica, los valores obtenidos no dependen de la cantidad de métodos que se tengan en una clase dada. El valor óptimo es 1, lo cual significa que todos los métodos de la clase son abstractos, por lo tanto, todos exhiben un comportamiento polimórfico. En caso contrario, el valor menos deseado es el 0, el cual significa que ninguno de los métodos es abstracto, por lo tanto, no exhiben un comportamiento polimórfico.
4.5. Métrica FMFAC (Factor Medio de Flexibilidad de Arquitecturas de Clases)
Se ha definido una métrica para medir el factor de flexibilidad que tiene una arquitectura de clases. Esta métrica consiste en la suma de los FFC de la arquitectura del módulo entre el número total de clases. La expresión matemática de la métrica FMFAC se muestra a continuación:
En donde:
ΣFFC = Sumatoria del Factor de Flexibilidad de Clase.
Tc = Total de clases en la arquitectura.
De la misma manera el valor óptimo de FMFAC es 1, lo cual significa que todos los métodos de las clases de la arquitectura son virtuales, por lo tanto, todos exhiben un comportamiento polimórfico, y el valor menos deseado de FMFAC es el 0, el cual significa que ningún método de las clases de la arquitectura es virtual, por lo tanto, ninguno tiene un comportamiento polimórfico.
Todas estas métricas cumplieron con los requerimientos para establecerse como escalas ordinales, los cuales son: que sean de orden débil y que además se cumpla la propiedad de homomorfismo (Suze, 1992). Según la teoría de la medición, estos requerimientos sustentan a las métricas.
5. Discusión
Utilizando el lenguaje Java se programó el proceso de cálculo del conjunto de métricas presentado y se integró este código a un marco de métricas de calidad de software. Este marco automatiza varias métricas, para la medición de calidad del software orientado a objetos. Para la etapa de pruebas del marco de métricas de calidad desarrollado, se utilizaron dos casos de prueba, un “marco estadístico” y el sistema “PSPCenidet”. Se realizó el cálculo de las métricas manualmente, así como automáticamente mediante el marco de métricas de calidad de software. Comprobando que ambos valores obtenidos de manera manual y automática fueron los mismos.
El principal aporte de este desarrollo es el conjunto de métricas de calidad de software, para medir el factor de flexibilidad (FFC y FMFAC) y de herencia de implementación (FHI, FHIJ y FHIAC), en diseños arquitecturales de clases. La definición de estas métricas, servirá para medir el grado de cierto código desagradable (smell code) por herencia de implementación en código legado.
REFERÊNCIAS
Briand, L., El Emam, K., & Morasca, S. (1996). On the Application of Measurement Theory in Software Engineering. Empirical Software Engineering, 1(1), 61-88. doi: https://doi.org/10.1007/BF00125812 [ Links ]
Chawla, M. K., & Chhabra, I. (2013). Capturing OO Software Metrics to attain Quality Attributes - A case study. International Journal of Scientific & Engineering Research, 4(6), 359-363. [ Links ]
Chawla, S., & Nath, R.(2013). Evaluating Inheritanceand Coupling Metrics. International Journal of Engineering Trends and Technology, 4(7), 2903-2908. [ Links ]
Gary, F. (2010). Measurement Theory for Software Engineers. Recuperado a partir de https://courses.cs.ut.ee/2010/se/uploads/Main/measurement-theory.pdf [ Links ]
IEEE Standard Glossary of Software Engineering Terminology. (1990). IEEE Std 610.12-1990, 1-84. doi: https://doi.org/10.1109/IEEESTD.1990.101064
Pinto, A. (2015). Interface inheritance vs Implementation inheritance. Recuperado a partir de https://www.linkedin.com/pulse/why-prefer-interface-inheritance-implementation-adrain-pinto [ Links ]
Suze, H. (1992). Properties of software measures. Software Quality Journal, 1(4), 225-260. doi: https://doi.org/10.1007/BF01885772 [ Links ]
Suze, H. (1995). Properties of Object-Oriented Software Measures. Recuperado a partir de http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.27.7578&rep=rep1&type=pdf [ Links ]
Agradecimientos
Tecnológico Nacional de México/CENIDET, por el proyecto 6077.19-P “Generación y evaluación de servicios Web de aprendizaje” y al CONACyT por la beca nacional de Orlando Ortiz Gutierrez.
Recebido/Submission: 20/08/2019
Aceitação/Acceptance: 25/09/2019