Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação
versão impressa ISSN 1646-9895
RISTI no.spe4 Porto set. 2015
https://doi.org/10.17013/risti.e4.16-34
ARTÍCULOS
Índices de Nuclearidad (Completo y Reducido), como aportación a la Teoría de Conceptos Nucleares
Nuclearity Indexes (Full and Reduced), as a contribution to the Theory of Nuclear Concepts
Juan Ángel Contreras1, Juan Arias Masa2, Ricardo Luengo González3, Luis Manuel Casas García4
1 Profesor Colaborador de la Universidad de Extremadura, Centro Universitario de Mérida, 06800, Mérida, España. E-mail: jaconvas@unex.es
2 Profesor Titular Escuela Universitaria de la Universidad de Extremadura, Centro Universitario de Mérida, 06800, Mérida, España. E-mail: jarias@unex.es
3 Catedrático de Universidad de la Universidad de Extremadura, Facultad de Educación, 06071, Badajoz, España. E-mail: rluengo@unex.es
4 Profesor contratado doctor de la Universidad de Extremadura, Facultad de Educación, 06071, Badajoz, España. E-mail: luisma@unex.es
RESUMEN
En este artículo se introduce un nuevo modo de medir el grado de importancia que tienen los conceptos a los que se hace referencia en la teoría de los Conceptos Nucleares. Esta nueva teoría utiliza las Redes Asociativas Pathfinder para establecer redes cognitivas de conceptos y en las que se observa y cuantifica la relación de cada uno de los conceptos con respecto al conjunto de todos los demás conceptos, siendo considerados, como conceptos nucleares, sólo aquellos conceptos que tienen tres o más enlaces. Ello permite discriminar cuáles son los conceptos fundamentales de entre todos los conceptos analizados. Como entrada para construir esta red se utiliza una matriz triangular que se utiliza también para crear estos nuevos índices que se llamarán Índice de Nuclearidad Completo e Índice de Nuclearidad Reducido.
Palabras-clave: Índice de Nuclearidad; Redes Asociativas Pathfinder; Teoría de los “Conceptos Nucleares”.
ABSTRACT
In this paper a new way of measuring the degree of importance of the concepts referred to in the theory of Nuclear Concepts are introduced. This new theory uses Pathfinder Associative Networks to establish cognitive networks of concepts that can be observed and quantified the relationship of each of the concepts with respect to the all other concepts; they are being considered as nuclear concepts, only those concepts that having three or more links. This allows to discriminate which are the fundamental concepts of all the concepts discussed. As input to build this network a triangular matrix will also be used to create these new index and they will call Full Nuclearity index and Reduced Nuclearity index.
Keywords: Nuclarity Index; Pathfinder Associative Networks; Theory of the “Nuclear Concepts".
1. Introducción
Este trabajo incorpora mejoras en lo que se refiere a la definición de los conceptos importante o nucleares que se dan en la Teoría de los Conceptos Nucleares (Luengo, 2013), TCN en adelante, creada por los doctores D. Ricardo Luengo y D. Luis Manuel Casas en la tesis doctoral de este último (Casas, 2002) en la Universidad de Extremadura.
Según la TCN, un concepto nuclear es aquel concepto importante que los usuarios tienen más anclados en su mente y que utilizan para poder realizar definiciones de otros conceptos, es decir, conceptos a través de los cuales se organizan los demás. Según los autores de esta teoría un concepto se considera nuclear cuando tiene 3 o más enlaces utilizando las Redes Asociativas Pathfinder (Schvaneveldt, 1990), en adelante RAP, la cual sirve para definir las estructuras cognitivas.
Algunos autores como Fenker (1975), Jonassen (1990), Preece (1976) y Shavelson (1972) están de acuerdo en que procedimientos o técnicas similares a las Redes Asociativas Pathfinder, como son: el Análisis de Componentes Principales, el Análisis de Cluster o el Escalamiento Multidimensional, sirven para definir las estructuras cognitivas.
Esta RAP se puede crear y dibujar utilizando, entre otros, el programa software llamado Goluca (Godinho, 2007).
Cuando existen pocos conceptos que forman la RAP es sencillo determinar cuáles son los conceptos nucleares; por ejemplo, realizando un simple vistazo a la red y viendo cuáles son los que tienen mayor número de enlaces. Pero cuando el número de nodos comienza a ser mayor en la RAP, distinguir cuales son los conceptos nucleares y sobre todo cuáles son más importantes o más nucleares que otros es muy complicado y se hace bastante tedioso y dificultoso. Este fue uno de los problemas y conclusiones obtenidas en el trabajo de (Contreras, Luengo, Arias, Casas, 2014). En el mismo trabajo, utilizando una metodología cualitativa, se estudiaron las memorias de verificación de los títulos de Grado en Informática, en 18 universidades españolas, con el objetivo de buscar los conceptos básicos o fundamentales que deben estudiar los alumnos en la materia de Base de Datos. Se obtuvo como resultado un total de 90 conceptos y se analizaron utilizando una metodología cuantitativa, las redes RAP; determinándose que 70 de todos estos conceptos eran los conceptos básicos o nucleares. Al ser tantos los conceptos estudiados, se necesitaba graduar cuales eran más importantes que otros en aquellos casos en el que el número de enlaces en la RAP fuese el mismo.
Es importante también diferenciar, por algún o alguna otra justificación, en el caso de tener distintos conceptos con el mismo número de enlaces, cuál de ellos tiene más importancia que otro.
Por tanto, en este artículo intentamos matizar esta definición de nuclearidad de los conceptos de tal forma que se pueda distinguir, ya no sólo, cuáles son los conceptos nucleares con rotundidad, sino definir también el grado de nuclearidad de dichos conceptos, permitiendo así calibrar la importancia de cada uno de ellos con respecto a los demás. Para ello vamos a continuar el trabajo realizado en (Contreras, Luengo, Arias, Casas, 2014) y vamos a definir un nuevo elemento de discriminación de los conceptos que llamaremos Índice de Nuclearidad para los conceptos nucleares.
2. Fundamentos. La teoría de los Conceptos Nucleares
Para los doctores Casas y Luengo, los creadores de la TCN, esta teoría es una "propuesta de integración". La razón es que tiene su fundamento en otras anteriores, particularmente las de (Piaget, 1978) o (Ausubel, Novak & Hanesian, 1978), basándose en muchas de sus ideas, y recogiendo aportaciones de otros campos y de los resultados de investigación.
Los elementos fundamentales del modelo de la TCN se explicaran a continuación. Para la TCN disponemos de al menos dos herramientas básicas como son las RAP y el programa Goluca.
Los puntos en los que difieren con las ideas de Piaget, Ausubel y Novak proponiendo alternativas nuevas (Luengo, Casas, Mendoza & Arias, 2011) los recogemos en los siguientes apartados.
2.1. Organización geográfica del conocimiento
Según describen los autores en (Casas, 2002), (Casas & Luengo, 2003b), (Casas & Luengo, 2004a), (Casas & Luengo, 2004b), (Casas & Luengo, 2005) y en (Casa & Luengo, 2013), su nueva propuesta teórica parte de una idea muy sencilla, la adquisición del conocimiento y su almacenamiento en la estructura cognitiva, en términos generales, sigue un proceso análogo a la adquisición del conocimiento del entorno físico.
También describen que esta adquisición se puede producir en tres etapas:
- Por la adquisición de ciertos “hitos”.
- Por la adquisición del conocimiento de una ruta, que es la capacidad de navegar en un hito a otro.
- Por la adquisición de una visión de conjunto, es decir, conocer todas las conexiones entre los hitos a través de las rutas.
2.2. Conceptos Nucleares
La teoría de estos autores propone que hay ideas de nivel superior, llamadas inclusores que sirven como anclaje para otras. A estas ideas es a las que se refieren al afirmar que es necesario, para lograr un mejor aprendizaje y la retención del material lógicamente significativo y nuevo, la disponibilidad dentro la estructura cognoscitiva de ideas de afianzamiento específicamente pertinentes a un nivel de inclusividad adecuado.
Según esta teoría, los conocimientos no se van organizando a partir de conceptos más inclusivos a otros más sencillos. Esto quizá ocurra al final, cuando se tiene una visión de conjunto, pero no al principio del conocimiento. Se produce por un sistema de "acrecentamiento", tal como el señalado por Rumelhart (Rumelhart, 1980), primero hitos del paisaje, después rutas y después visión general del mapa.
2.3. Senderos de mínimo coste
Al analizar, los autores, los datos experimentales (Casas, 2002), mientras mayor es la edad de los alumnos y más avanza su aprendizaje, más simples aparecen las representaciones de las relaciones entre conceptos que se obtienen con las RAP.
Se puede interpretar este hecho considerando que, a pesar de que en la estructura cognitiva del alumno aparecen cada vez más elementos y más relaciones entre ellos, se utilizan subestructuras cada vez más simples y más significativas, a lo que se denomina "senderos de mínimo coste". Como ocurre en otros aspectos vitales, la estructura cognitiva funciona por un principio de mínima energía.
3. Definiciones
En primer lugar, para el cálculo de estos índices, es necesario plasmar el entorno y las informaciones de que disponemos.
3.1. Entorno y necesidad de información
El elemento fundamental de información que se necesita para construir la RAP, antes de aplicar los algoritmos necesarios, es lo que llamamos la matriz de proximidad. Esta matriz está compuesta de filas y columnas que corresponden a los conceptos que se desean analizar y de donde saldrán los conceptos nucleares. Cada celda de la matriz contiene un valor numérico indicando la relación de proximidad que tienen los dos conceptos de la fila y columna que indexan esa celda, teniendo en cuenta que un valor alto significa que los conceptos están muy relacionados; un valor bajo indica que los conceptos están poco relacionados; y un valor de 0 indica que no hay relación alguna entre el par de conceptos. Esta matriz es simétrica, ya que tiene los mismos elementos y en el mismo orden, tanto en las filas como en las columnas. Por lo tanto, el valor para la fila i y la columna j, para un valor de i < > j, es el mismo que el valor de la fila j y la columna i. Además, el valor de la fila i y de la columna j, para un valor de i = j, no tiene mayor interés (o tendrá un valor 0), ya que indica la relación de un elemento consigo mismo.
La información de esta matriz de proximidad la toma como entrada el algoritmo Pathfinder para construir la RAP, dando como resultado otra matriz a la que llamamos matriz Pathfinder. Esta matriz Pathfinder, a su vez, la toma como entrada un algoritmo de dibujo de redes, como por ejemplo el creado por Kamada y Kawai (1989), para dibujar la red y se puedan observar en ella los enlaces que tiene cada uno de los conceptos (nodos) de la red. En esta red resultante un concepto (un nodo) es nuclear si tiene tres o más enlaces con otros tantos conceptos (nodos).
Sólo necesitamos la matriz de proximidad para obtener la información para construir los nuevos índices de Nuclearidad, ya que en ella tenemos la información recogida del pensamiento que tienen los sujetos sobre cada par de conceptos, tal cual se les ha presentado en el interfaz que recoge la información para la toma de datos.
Un problema previo con el que nos encontramos es buscar o construir la matriz de proximidad, es decir, ¿de dónde extraemos la información para rellenar dicha matriz? Esta información, hasta ahora, la estamos recopilando por dos vías distintas:
- Preguntando directamente a los alumnos el grado de relación entre cada pareja de conceptos. Esto lo podemos realizar utilizando el propio programa Goluca1 citado anteriormente, o bien por el software Meba2 construido por el doctor D. Juan Arias para su tesis doctoral (Arias, 2007).
Obteniendo la información a través de algún software de análisis cualitativo. Por ejemplo, el software webQDA3 (Souza, Costa & Moreira, 2011), nos proporciona directamente dicha matriz de proximidad una vez que hemos realizado el análisis cualitativo pertinente. También existen otras formas de análisis tal como indica (Julia, Daniel Caballero; Galindo, Purificación Vicente; Villardón & Mª Purificación Galindo, 2014)
- Alguna información utilizada en este artículo para el cálculo del índice de Nuclearidad está recogida del trabajo realizado en una investigación cualitativa anterior, utilizando precisamente este software, y que se expone en (Contreras, Luengo, Arias & Casas, 2015).
A continuación, nos vamos a centrar en este segundo método ya que, a través del software webQDA, tendremos toda la información necesaria para calcular el índice de Nuclearidad.
3.2. Elementos a tener en cuenta en los distintos índices de la fórmula
Partiremos de la matriz de proximidad para definir los parámetros que necesitamos para crear las fórmulas del índice de Nuclearidad de cada concepto.
Los elementos que son necesarios para construir los parámetros de las fórmulas son:
- Número total de fuentes (lo llamaremos TF): Es el número total de documentos, o fuentes utilizadas de información, sobre los que se va a realizar la investigación y de las cuales se van a extraer los conceptos necesarios sobre los que se van a calcular los índices de Nuclearidad.
- Frecuencia (la llamaremos F): Es el número de veces que ha sido referenciado un concepto entre todas las distintas fuentes de información utilizadas. Es posible que un concepto sea referenciado en una misma fuente más de una vez.
- Frecuencia máxima (la llamaremos FMAX): es el valor máximo de la frecuencia anterior F.
- Número de conceptos (llamaremos N): es el numeró total de conceptos obtenidos al realizar la investigación. Coincide con el número de filas o también con el número de columnas de la matriz de proximidad.
- Número de Fuentes por conceptos (lo llamaremos NF): es el número de fuentes distintas en el que han aparecido cada uno de los conceptos estudiados.
- Número de Vecinos (lo llamaremos NV): es un número que indica con cuantos conceptos ha establecido relación cada uno de los conceptos, sin contar la relación consigo mismo. Recordemos que en la matriz de proximidad tenemos los valores del grado de relación de cada par de conceptos, por tanto, sumaremos bien por fila o bien por columna, el número de veces que aparece un valor distinto de cero, queriendo decir con ello que existe una relación entre ese par de conceptos y, por tanto, es un vecino.
- Suma de proximidad (lo llamaremos SP): es la suma, bien por fila o bien por columnas, de los valores de las relaciones o fortaleza que tiene cada vecino con todos los demás. Es decir, la suma de los valores de las celdas de la matriz de proximidad de cada concepto, bien por filas, o bien por columnas.
- Suma de proximidad máximo (lo llamaremos SPMAX): es el valor máximo de todas las sumas de proximidad anterior, SP.
3.3. Creación de los índices de las fórmulas
Con los elementos anteriores construiremos cuatro índices auxiliares que van a servir para componer las fórmulas fundamentales; y después, procederemos a normalizar dichos índices auxiliares para que no distorsionen en la fórmula alguno de ellos sobre los otros. Es decir, consideraremos que cada uno de estos índices auxiliares tiene la misma importancia relativa con respecto a los demás. Para cada uno de los valores estos índices utilizaremos seis dígitos decimales, ya que obtendremos valores comprendidos entre 0 y 1.
A continuación exponemos cada uno de ellos:
- Índice de Frecuencias (IFREC): para cada concepto, se corresponde con la división de la frecuencia del concepto (F) dividido por la frecuencia máxima de entre todos los conceptos (FMAX). Con ello obtenemos un valor decimal entre 0 y 1; indicando que los valores próximos a 1 son conceptos relativamente muy frecuentemente utilizados en relación a los demás conceptos, y un valor cercano al 0, indica que es un concepto que no es relativamente tan frecuentemente utilizado con respecto al resto de conceptos tratados. Por tanto, este índice nos indica la utilización de cada uno de los conceptos de la investigación, a mayor utilización el concepto es más importante. La fórmula sería:
- Índice de Fuentes (IFUEN): Es necesario conocer también el índice de utilización de los conceptos con respecto al número total de documentos diferentes en los que se ha utilizado el mismo; ya no sólo cuantas veces ha sido utilizado, como nos muestra el índice anterior, sino la calidad con la que ha sido utilizado, es decir, en cuantos documentos distintos han sido utilizado cada uno de los conceptos. Esto lo vamos a realizar dividiendo el número de fuentes donde ha sido utilizado cada concepto (NF) entre total de fuentes existentes utilizadas (TF). Obtendremos un valor decimal entre 0 y 1; indicando un valor alto que un concepto ha sido utilizado en un número importante de documentos, y un valor cercano a 0 que el concepto ha sido utilizado en pocos documentos. La fórmula sería:
- Índice de Vecindad (IVEC): lo calcularemos dividiendo el valor del número de vecinos (NV) de cada concepto entre el número total de conceptos (N) menos 1, ya que para este índice no se tiene en cuenta la relación de cada concepto consigo mismo. Es decir, N-1 es el número máximo de vecinos que puede tener cada concepto, por ello lo dividimos entre este valor. Obtendremos un valor decimal entre 0 y 1; indicando un valor próximo a uno que el concepto tiene muchas relaciones con otros conceptos, y un valor próximo a 0 que tiene pocas relaciones con otros conceptos. La fórmula seria la siguiente:
- Índice de Proximidad (IPROX): lo calcularemos dividiendo la suma de proximidad de cada concepto (SP) entre el valor máximo de la suma de proximidad de todos ellos (SPMAX). Con ello obtendremos la fuerza de la relación entre conceptos. Obtendremos un valor decimal entre 0 y 1; indicando un valor próximo a 1 que la relación entre los conceptos es muy fuerte, y un valor próximo a 0 que la relación entre conceptos es débil. La fórmula sería la siguiente:




3.4. Unificación de la importancia de los índices
Todos los índices van a tener la misma importancia. Y para que alguno de ellos no distorsione el resultado final de los Índices de Nuclearidad vamos a normalizarlos.
La normalización la llevaremos a cabo de la siguiente forma: por cada uno de los índices vamos a calcular el valor de la diferencia entre el valor máximo del índice y el valor mínimo del índice, y a esto lo vamos a llamar Delta para cada índice. Posteriormente realizaremos dos sumas, por un lado sumaremos todos los deltas anteriores y nos dará un Delta total, y por otro sumaremos sólo los deltas de los índices de vecinos y suma de proximidad y nos dará un Delta parcial. Con estos dos deltas distintos podremos crear posteriormente una fórmula para el índice de Nuclearidad Completo y otra fórmula para el índice de Nuclearidad Reducido. Después con los Deltas vamos a calcular los Pesos, es decir, la significación de cada Delta de cada índice con respecto al Delta total o parcial. Con ellos normalizamos, con respecto a 100, todos los valores de los índices anteriores calculados.
A continuación, explicamos los pasos anteriores:
- Cálculo de los Delta para cada índice: IFrecmax es el valor máximo obtenido en la aplicación de la formula (1) e IFrecmin es el valor mínimo obtenido de la aplicación de la formula (1). IFuenmax es el valor máximo obtenido en la aplicación de la formula (2) e IFuenmin es el valor mínimo obtenido de la aplicación de la formula (2). IVecmax es el valor máximo obtenido en la aplicación de la formula (3) e IVecmin es el valor mínimo obtenido de la aplicación de la formula (3). IProxmax es el valor máximo obtenido en la aplicación de la formula (4) e IProxmin es el valor mínimo obtenido de la aplicación de la formula (4). Por tanto:
- Cálculo de los Deltas total y parcial: el primero correspondiente a la suma de los cuatro Deltas anteriores y llamaremos Dtotal, y el segundo correspondiente sólo a los Deltas del índice de vecinos y del índice de proximidad, y llamaremos Dparcial. Aquí mostramos dicho cálculo:
- Cálculo de los Pesos en porcentajes con el Dtotal para cada uno de los índices: Con los Dtotal podemos calcular los pesos en % de cada uno de los índices. Hay tener en cuenta, que vamos a tener dos tipos de pesos, y los pesos en este caso se utilizarán para la fórmula Completa. El cálculo se realiza de la siguiente forma:
- Cálculo de los Pesos en porcentajes con el Dparcial para cada uno de los índices: Con los Dparcial podemos calcular los pesos en % de cada uno de los índices. Hay tener en cuenta, que vamos a tener dos tipos de pesos, y los pesos en este caso se utilizarán para la fórmula Reducida. El cálculo se realiza de la siguiente forma:
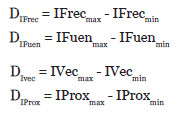
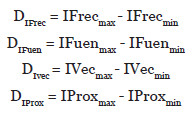
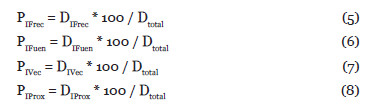

4. Formulación
Vamos a definir las fórmulas de los Índices de Nuclearidad en formato completo y en formato reducido.
El formato completo constituye la forma natural de realizar el cálculo del índice y en él se incluyen todos los elementos necesarios, y creemos, influyentes para este índice. Sería, digamos, la forma ideal de discernir la importancia de cada uno de los conceptos en relación con todos los elementos que intervienen en las investigaciones en la que se encuadra lo que estamos buscando. Para ello, definiremos lo que vamos a llamar Índice de Nuclearidad Completo (lo llamaremos INC).
Entendemos que disponer de toda la información que interviene en el cálculo del Índice de Nuclearidad Completo no siempre es posible, por lo que vamos a definir también para estos casos el Índice de Nuclearidad Reducido (lo llamaremos INR). Consideramos que este último índice contempla dos de los elementos importantes para discernir la importancia entre conceptos, es decir: cuantos vecinos tienen cada uno de los conceptos y como de fuerte es la relación entre ellos.
Tanto uno como el otro permiten graduar la importancia de los conceptos nucleares, estableciendo un orden de importancia entre ellos, naturalmente el completo con más información que el reducido.
4.1. Fórmula del INC
Para el cálculo del INC van a intervenir los resultados de las fórmulas con números (1), (2), (3), (4), (5), (6), (7) y (8) de la siguiente forma:
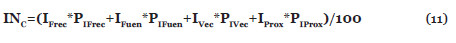
4.2. Fórmula del INR
Para el cálculo del INR van a intervenir los resultados de las formulas con números (3), (4), (9) y (10) de la siguiente forma:
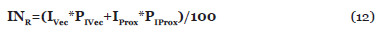
5. Ejemplificación
5.1. Introducción
Vamos a poner un ejemplo, desde el comienzo, para comprobar la construcción y los resultados del cálculo del índice de Nuclearidad Completo y Reducido.
La fuente de información va a ser el programa de análisis estadístico WebQDA. Compararemos también los resultados obtenidos de nuestra formulación con los datos obtenidos en el software analítico de Goluca.
5.2. Elementos de información necesarios
Partimos de una investigación cualitativa que corresponde al estudio de los contenidos básicos de Base de Datos en las memorias de verificación de los títulos universitarios de los Grados en Informática realizada con el software WebQDA (Contreras, Luengo, Arias & Casas, 2014). Construiremos los elementos básicos de información para calcular las partes que componen las fórmulas de los índices de Nuclearidad. En concreto, de la investigación sólo vamos a coger la parte correspondiente al grupo de conceptos llamado “Modelo Relacional”.
El número de memorias de verificación utilizadas (TF), como podemos ver en la figura 1. Ejemplo de fuentes utilizadas., han sido 22, por lo que el parámetro llamado Total de Fuentes se corresponde con esta valor (TF=22).

Los conceptos encontrados en la investigación (N) los podemos ver en la figura 2. Conceptos obtenidos de la investigación.. El Número de Conceptos han sido 14, por lo que el parámetro llamado Número de Conceptos se corresponde con este valor (N=14).
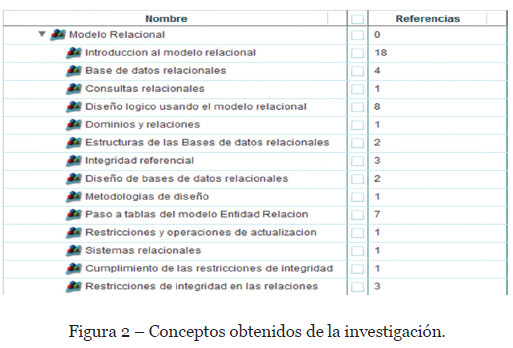
La frecuencia de cada concepto (F), la podemos observar en la columna Referencias también en la figura 2. Conceptos obtenidos de la investigación.. Por lo que la frecuencia máxima de todas ellas la representa el concepto llamado “Introducción al modelo relacional” con un valor de 18 (Fmax=18).
El número de fuentes (NF) por concepto lo extraemos también desde el software WebQDA utilizando los valores de la diagonal principal de la matriz de proximidad que nos proporciona un tipo de consulta llamada “Consulta de Matrices Triangulares”. Podemos observar estos valores en la figura 3. Matriz de proximidad y número de fuentes por cada concepto.. Por ejemplo, para el concepto “Introducción al modelo relacional” el valor es de 14 (NF=14). Así obtendremos este valor para cada uno de los conceptos.

Los otros parámetros que necesitamos son el número de vecinos por cada concepto (NV), la suma de proximidad (SP) por cada concepto y la suma de proximidad máxima (SPmax). Los dos primeros los obtendremos de la matriz de proximidad de la figura 3. Matriz de proximidad y número de fuentes por cada concepto.. Transformaremos la misma para calcular estos valores, de tal forma que: los valores de la diagonal principal sean ceros y traspondremos cada una de las filas en cada columna. El resultado de dicha matriz podemos observarlo en la figura 4. Matriz de proximidad completa y traspuesta.
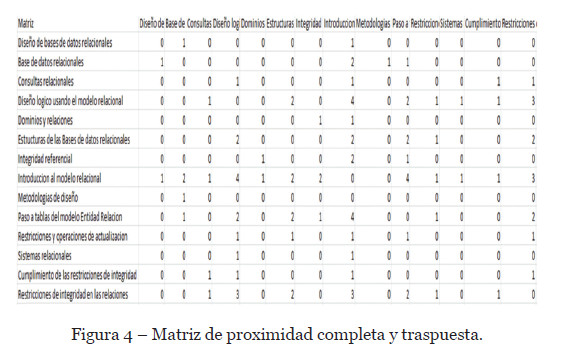
Para el cálculo del parámetro de vecinos para cada concepto (NV), sumaremos por fila, los valores distintos de cero de cada columna de la matriz de la figura 4 Matriz de proximidad completa y traspuesta. Podemos observar, que para el concepto “Diseño de Base de datos relacionales” (fila 1), la columna de Base de datos relacionales tienen valor 1 y la columna de Introducción al modelo relacional tiene valor 1, es decir, estas dos columnas son las únicas con valores distinto de cero, por lo que el valor de NV para este concepto en esa fila es 2 (NV=2). Esto lo haremos para cada fila.
Continuando con la figura 4. Matriz de proximidad completa y traspuesta., obtendremos el valor de la suma de proximidad (SP) por cada concepto sumando los valores de cada columna de esa fila. Siguiendo el mismo ejemplo anterior, podemos observar, para el concepto “Diseño de Base de datos relacionales” (fila 1), la columna de Base de datos relacionales tienen valor 1 y la columna de Introducción al modelo relacional tiene valor 1, y el resto de columnas tiene valor de 0, es decir, la suma de todos estos valores para ese concepto es 2 (SP=2). Esto lo haremos por cada fila.
Podemos observar el resultado final del cálculo de las sumas de proximidades por conceptos en la figura 5. Suma de proximidad por concepto..
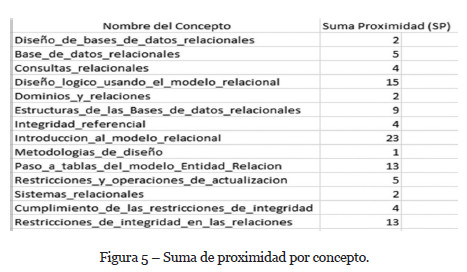
El parámetro valor máximo de la suma de proximidad (SPmax) en la figura 5. Suma de proximidad por concepto., corresponde al concepto “Introducción al modelo relacional” con un valor de 23 (SPmax=23).
5.3. Cálculo de los índices necesarios
Para calcular los índices de frecuencias (IFREC), índices de fuentes (IFUEN), índice de vecinos (IVEC) e índice de proximidad (IPROX), aplicaremos las fórmulas anteriores (1), (2), (3) y (4) respectivamente para cada uno de los 14 conceptos obtenidos.
Teniendo en cuenta que la Frecuencia Máxima (Fmax) es 18, la Suma de Proximidad máxima (SPmax) es 23, el Número Total de Fuentes (TF) es 22 y el Número Total de Conceptos (N) es 14, el resultado de aplicar las fórmulas anteriores lo observamos en la siguiente figura 6. Valor de los índices de cada concepto. Los valores de cada uno de ellos están comprendidos en el rango entre 0 y 1.
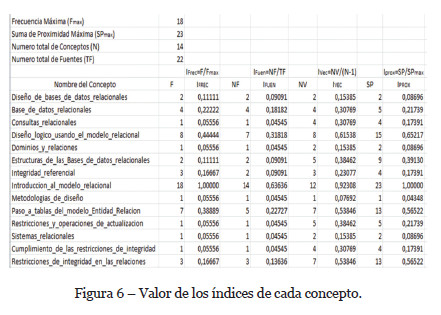
5.4. Cálculo de los Deltas y de los Pesos
Para el cálculo de los Deltas de cada índice utilizaremos las formulaciones anteriores siguientes:
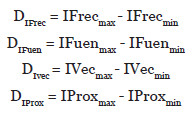
Por tanto, el valor de cada Delta es el siguiente:
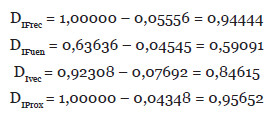
Ya podemos calcular el Delta total y el Delta parcial aplicando la siguiente fórmula:
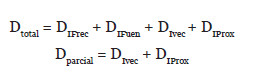
Por tanto, los resultados son los siguientes:
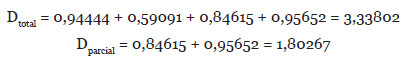
Ya podemos calcular los pesos de cada uno de los índices, para el índice de Nuclearidad Completo, utilizando las fórmulas anteriores numeradas con (5), (6), (7) y (8). El resultado de aplicar estas fórmulas es el siguiente:
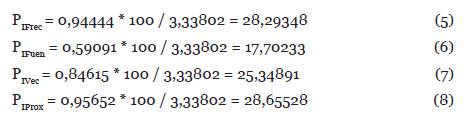
De la misma forma podemos hacerlo para calcular el índice de Nuclearidad Reducido. Para ello utilizaremos las fórmulas numeradas con el (9) y el (10). El resultado de aplicar estas fórmulas es el siguiente:
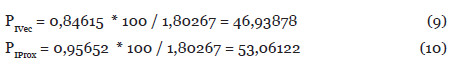
5.5. Cálculo del Índice de Nuclearidad Completo
Teniendo en cuenta el cálculo de los valores anteriores, a continuación realizamos el cálculo del Índice de Nuclearidad Completo para cada concepto.
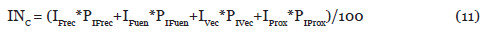
Aplicando la fórmula (11), los datos del Índice de Nuclearidad Completo lo tenemos en la columna INc de la Figura 7. Tabla de Índices de Nuclearidad.
5.6. Cálculo del Índice de Nuclearidad Reducido
Teniendo en cuenta el cálculo de los valores anteriores, a continuación realizamos el cálculo del Índice de Nuclearidad Reducido para cada concepto.
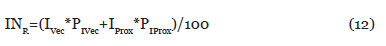
Aplicando la fórmula (12), los datos del Índice de Nuclearidad Reducido, podemos observarlos en la columna INr de la Figura 7. Tabla de Índices de Nuclearidad.
5.7. Conceptos Nucleares obtenidos en el Software “Goluca”
Recordemos que los creadores de la TCN consideran un concepto nuclear cuando tiene tres o más vecinos una vez construida la RAP. Y como comentamos anteriormente el software “Goluca” nos proporciona esta información de Nuclearidad de los conceptos.
Para el ejemplo que nos ocupa, el resultado de Nuclearidad de los conceptos obtenidos desde el software “Goluca” lo podemos observar en la Figura 8 Imagen Gráfica de Conceptos Nucleares en Goluca.
En ella se puede observar cuáles son los conceptos nucleares mediante la observación del color y tamaño de los nodos. El concepto nuclear tiene un color amarillo o naranja.
El software “Goluca”, también nos proporciona esta información solicitándosela al mismo mediante una opción de menú.
6. Comparación de resultados
Seguiremos manteniendo, tal como indican los autores de la TCN, que los conceptos son nucleares cuando tienen 3 o más enlaces. Añadiremos además, los resultados de los índices para determinar cuál es más nuclear que otro.
En la Figura 9. Resumen de resultados. hemos resumido los resultados obtenidos junto con los vecinos que tienen cada uno de los conceptos y así poder comparar los resultados de los índices con los resultados obtenidos por el software “Goluca”.
También hemos incorporado en esa figura, el orden de Nuclearidad en el que quedarían cada uno de los conceptos en cada uno de los casos.
Podemos observar que los conceptos no nucleares (“Diseño de Base de Datos Relacionales”, “Dominios y Relaciones”, “Metodologías de Diseño” y “Sistemas Relacionales”) se siguen manteniendo en ambos sistemas de medición. Excepto el concepto “Integridad Referencial” que, para nuestro índice sí es nuclear, aunque lo es en los últimos lugares, para el software Goluca no lo considera nuclear.
Los conceptos más nucleares (“Introducción al modelo Relacional” y “Diseño Lógico Usando el Modelo Relacional”) también se mantienen en ambos sistemas. Para el resto de conceptos la graduación es distinta en ambos sistemas.
Para el Índice de Nuclearidad Completo hemos conseguido establecer más diferencias entre conceptos. Por ejemplo, siguiendo la columna titulada orden 4 de la Figura 9. Resumen de resultados., no hay distinción entre los conceptos
numerados con valores 4, 5 y 6. Sin embargo, con el Índice de Nuclearidad Completo, en columna llamada orden 1, eso sólo sucede en los últimos lugares, es decir, el concepto numerado con valor 9.
El índice de Nuclearidad Reducido, aunque mejora la graduación de la nuclearidad con respecto al proporcionado por el software Goluca, es menos preciso que el índice de Nuclearidad Completo. Podemos observarlo viendo la columna orden 2 de la Figura 9. Resumen de resultados. No podemos distinguir los conceptos ordenados con valor 3 y 7 ya que el valor del índice es el mismo, esto sólo sucede una vez en el índice de Nuclearidad Completo.
7. Conclusiones
Hemos conseguido la diferenciación cuantitativa de conceptos a través del Índice de Nuclearidad Completo (INc). Es cierto también, que los valores en la matriz de proximidad son bajos, valores entre 1 y 4, lo que hace más complicado tal diferenciación. Por ello, aconsejamos que los valores en la graduación de los conceptos que intervienen en la matriz de proximidad, al menos, tengan valores entre 0 y 100, aunque es preferible que los tengan entre 0 y 1000. Ello mejoraría los índices de Nuclearidad. Aun teniendo en cuenta esto, el INc funciona mejor que realizar sólo el conteo de los nodos vecinos para establecer los conceptos nucleares.
El Índice de Nuclearidad Reducido (INr) solo debe utilizarse cuando no sea posible tener toda la información necesaria de los parámetros que intervienen en el INc. Es sólo un índice auxiliar, que mejora el sistema de conteo de los nodos vecinos, pero que como se aprecia en la Figura 9. Resumen de resultados., en algunos casos, no distingue tan bien como lo hace el INc.
También hemos conseguido mejorar los contenidos que pueden llevarse a efecto (si implementan) en los programas software de análisis Goluca y WebQDA, por lo que sería interesante que los mismos incorporaran estos índice e implementaran entre sus mejoras esta formulación para que puedan ser utilizados por los investigadores que los usen de una forma directa sin tener que realizar ningún cálculo adicional por ellos mismos. En definitiva, facilitar a los investigadores el uso de estos dos índices.
8. Referencias
Arias, Juan. (2007). Evaluación de la calidad de Cursos Virtuales: Indicadores de Calidad y construcción de un cuestionario de medida. Aplicación al ámbito de asignaturas de Ingeniería Telemática. Badajoz.
Ausubel D.P., Novak J.D. y Hanesian H. (1978). Psicologia educativa: un punto de vista cognoscitivo. Ed. Trillas. México (trd versión en inglés del 1978). [ Links ]
Casa L. y Luengo R. (2013). The study of the pupil´s cognitive structure: the concept of angle. Eur J Psychol Educ 28, pp.373-398 Springer (DOI 10.1007/s10212-012-0119-4). [ Links ]
Casas L. (2002). El estudio de la estructura cognitiva de los alumnos a traves de redes asociativas Pathfinder. Aplicación y posibilidades en Geometría. Memoria para el Titulo de Doctor. Badajoz, España: Universidad de Extremadura.
Casas L. y Luengo R. (2003b). Matemáticas: Representaçao Da estructura Cognitiva de Alunos. Evora, Portugal: Congresso de Neurociencias Cognitivas. Universidade de Évora.
Casas L. y Luengo R. (2004a). Teoría de los Conceptos Nucleares. Aplicación en Didáctica de las Matemáticas. Badajoz: R. Luengo, lineas de investigación en Educación Matemática. Servicio de publicciones FESPM. [ Links ]
Casas L. y Luengo R. (2004b). Representación del conocimiento y aprendizaje. Teoría de los conceptos nucleares. Revista Española de pedagogía, n. 227, pag. 59-84. [ Links ]
Casas L. y Luengo R. (2005). Conceptos nucleares en la construcción del concepto de ángulo. Enseñanza de las Ciencias, n. 23 (2), pag. 201-216. [ Links ]
Contreras J.A., Luengo R., Arias J., Casas L.M. (2014). Análisis cualitativo y cuantitativo de las materias básicas de base de datos en las memorias de verificación de los títulos universitarios de Grado en Informática en las Universidades Españolas. (AISTI, Ed.) RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação (ISSN: 1646-9895), E2(09-2014), pp. 37-53. doi: 10.17013/risti.e2.37-53 [ Links ]
Contreras, J.A.; Luengo, R.; Arias,J. y Casas. L.M. (2015). Indice de Nuclearidad para la toria de los Conceptos Nucleares. 4ª Congreso Ibero-Americano en investigación cualitativa. Aracaju (Brasil).
Contreras, Juan Angel; Luengo, Ricardo; Arias, Juan; Casas, Luis Manuel. (2014). Análisis mixto, cualitativo-cuantitativo, de los contenidos básicos de las materias de base de datos en los Planes de Estudio Universitarios de Grado en Informática en la Universidad de Extremadura. En A. P. otros (Ed.), 3º Congreso Ibérico en Investigación Cualitativa. vol 1, pp. 138-142. Badajoz (España): Ludomedia. [ Links ]
Fenker R.M. (1975). The organization of conceptual materials: A methodology for meassuring ideal and actual cognitive structures. Instructional Science, 4, pp. 33-57. [ Links ]
Godinho V. (2007). Implementación del Software Goluca y aplicación al cambio de redes conceptuales. Memoria de Diploma de Estudios Avanzados. Badajoz, España: Universidad de Extremadura.
Jonassen D.H. (1990). Semantic network elicitation: tools for structuring hypertext. Hypertext: State of the Art. Oxford: Intellect. [ Links ]
Julia, Daniel Caballero; Galindo, Purificación Vicente; Villardón, Mª Purificación Galindo. (2014). Grupos de Discusión y HJ-Biplot: Una Nueva Forma de Análisis Textual. (AISTI, Ed.) RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação (ISSN: 1646-9895), e2(09/2104), pp. 19-35. doi: 10.17013/risti.e2.19-35 [ Links ]
Luengo R. (2013). La teoría de los conceptos nucleares y su aplicación de la investigación en la didáctica de las Matemáticas. Revista Iberoamericana de Educación Matemática(34), pp. 9-36. [ Links ]
Luengo R., Casas L., Mendoza M. y Arias J. (2011). Posibilities of "Nuclear Concepts Theory" on Educacional Research, a Review. Florencia, 16-17 de Junio de 2011: International Conference The Future of Education.
Piaget J. (1978). La evolución intelectual entre la adolescencia y la edad adulta. J Delval comp. Lecturas de Psicología del niño, V 2. [ Links ]
Preece P. (1976). Mapping cognitive structure: A comparison of methods. Journal of Educational Psychology, 68, pp. 1-8. [ Links ]
Rumelhart D.E. (1980). Schemata: The building block of cognition. R.J. Spiro, B.C. Bruce y W. Brewer.Theoretical issues in reading comprehesion. Hillsdale, NJ: Erbaum. [ Links ]
Schvaneveldt R.W. (1990). Pathfinder Associative Networks: Studies in Knowlegde Organization. Norwood, New Jersey, EEUU: ABLEX Publishing Corporation. [ Links ]
Shavelson R. (1972). Some aspects of the correspondence between content structure and cognitive structure in physics instruction. Journal of Educational Psychology, 63, pp. 225-234. [ Links ]
Souza, F. N., Costa, A. P., & Moreira, A. (2011). Análise de Dados Qualitativos Suportada pelo Software WebQDA. VII Conferência Internacional de TIC na Educação: Perspetivas de Inovação, ( pp. 49-56). Braga (Bortugal). [ Links ]
T. Kamada and S. Kawai. (1989). An algorithm for drawing general undirected graphs. Information Processing Letters, 31, pp. 7-15. [ Links ]
Recebido / Recibido: 23/03/2015
Aceitação /Aceptación: 18/09/2015
NOTAS
1 Goluca es un software construido por el grupo de investigación Ciberdidact utilizado para realizar análisis de Redes Asociativas Pathfinder.
2 Meba es una aplicación software que entre sus muchas funciones, tiene una que pregunta la proximidad entre conceptos y genera de la matriz de proximidad.
3 webQDA es un software de apoyo para el análisis de datos cualitativos en un ambiente colaborativo y distribuido. Se accede en la siguiente dirección web www.webqda.com.