Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Encontros Científicos - Tourism & Management Studies
versão impressa ISSN 1646-2408
Encontros Científicos n.5 Faro 2009
Measuring the efficiency of banks using a two-stage DEA model
Ana Isabel Martins
PhD Candidate, Adjunct Professor, Escola Superior de Gestão, Hotelaria e Turismo
Universidade do Algarve, Faro, Portugal
ABSTRACT
Facing the biggest world-wide crisis of the last 30 years, significant losses in revenues are foreseen for the banking sector as well as an increasing competitive pressure. Using data from 2007, this study evaluates the efficiency of the 37 major banks operating in Portugal through DEA methodology. Efficiency is evaluated trough Chen and Zhu (2004) two-stage model applied to the banking industry, circumventing the usual problem inherent in the existence of two approaches (Production/Intermediation). The main contribution of this study is the incorporation of new variables that reflect, besides profitability, value creation and risk, such as intrinsic value added. It is usual to apply standard DEA models to each stage to typically two-stage processes. However, such an approach may conclude that two inefficient stages lead to an overall efficient DMU with the inputs of the first stage and outputs of the second stage. The distortion/improvement in the DEA frontier is caused by the presence of intermediate measures. Efficiency is analyzed under a global perspective including all banks, assuming that all access the same technology. Subsequent analysis is made to the efficiency by groups based on size/business and risk factors, estimated separate frontiers, analyzed the inefficiencies intra-groups and differences among groups.
Keywords: Data Envelopment Analysis; Two-Stage Models; Efficiency; Bank Efficiency; Efficiencies Matrix
A avaliação da eficiência dos bancos através de um modelo DEA bietápico
RESUMO
Enfrentando actualmente a maior crise mundial dos últimos 30 anos, prevêem-se para o sector bancário quebras significativas nas receitas e uma crescente pressão competitiva. Este estudo avalia a eficiência dos 37 principais bancos a operar em Portugal através da metodologia DEA segundo o modelo bietápico de Chen e Zhu (2004) aplicado ao sector bancário, contornando a habitual problemática inerente à existência de duas abordagens (Produção/Intermediação). A principal contribuição deste estudo consiste na incorporação de novas variáveis que reflictam, para além da rendibilidade, a criação de valor e o risco, como por exemplo, o valor intrínseco acrescentado. Neste tipo de processos, tipicamente bietápicos, é habitual a aplicação de modelos DEA standard a cada uma das etapas. Esse tipo de abordagem pode concluir que duas etapas ineficientes promovem uma DMU globalmente eficiente com os inputs da primeira e os outputs da segunda. A distorção da fronteira de eficiência é provocada pela existência de medidas intermediárias. A eficiência é analisada incluindo todos os bancos, admitindo que todos têm acesso à mesma tecnologia. Posteriormente é efectuada uma análise à eficiência por grupos, com base nos factores dimensão/negócio e risco, sendo estimadas fronteiras separadas, determinadas ineficiências intra-grupos e analisadas diferenças entre grupos.
Palavras-chave: Análise Envoltória De Dados; Modelos Bietápicos; Eficiência; Eficiência Bancária; Matriz De Eficiências
1. INTRODUCTION
Strong competition, high dynamics, increasing sophistication of services and a sharp drop in interest rates are factors that greatly contributed to the unquiet environment lived in recent years in the banking sector. Recent years have been characterized by a high competitive atmosphere in the banking sector, which strategic action focused on concentration, privatization, diversification, innovation and modernization of distribution network, products, work processes as well as organizational structures and image. Freedom of establishment and services within the European Union, established by Directive 2000/12/EC, dropped the most significant barrier to entry and internationalization, increasing the level of competition, compounded by the fact that non-bank institutions were able to provide banking services of financial intermediation, previously exclusive to banks, by removing regulatory restrictions. Participation in the Euro area and the resulting financial integration in an enlarged monetary union decisively conditioned the latest developments in the banking system and the behavior of the Portuguese economy in general. Taking into account these global trends, prospects are for the banking sector to increasing competitive pressure that may lead to further narrow margins and increased efficiency to maintain market share.
Although there is a growing trend of studies about financial sector productive efficiency, many of them focused only on traditional issues associated with scale and scope economies, not yet been properly explored deviations from the efficiency frontiers, also known in the literature as X-inefficiencies. Empirical evidence suggests that X-inefficiencies caused by managers inability to control costs or maximize revenues are greater than the costs associated with a poor choice of scale or product portfolio. X-inefficiencies are responsible, at least about 20% of production costs in the banking sector, while the scale and scope inefficiencies, when properly estimated, are responsible, no more than about 5% of costs (Berger et al., 1993).
There are several techniques used in efficiency studies. Data Envelopment Analysis (DEA) has been widely used in many different sectors, given its mathematical simplicity and its non-parametric nature. Evaluation of this extension can be made through the studies of Emrounejad and Thanassoulis (2001).
This study evaluates the efficiency of the main banks operating in Portugal trough DEA methodology. The main objective is to apply Chen and Zhu (2004) two-stage model, applied to the banking sector, incorporating new variables that reflect, besides profitability, value creation and risk (trough the opportunity cost for shareholders). Comparison of results among this model and traditional DEA models is made, as well as between the efficiency levels among different groups of banks. Besides this introduction, this study is structured as follow: section 2 discusses the main concepts and methodologies associated with the assessment of efficiency. Section 3 presents the main aspects of DEA methodology. Section 4 characterizes the sample, the DEA models used and the input/output variables. Section 5 presents the main results and section 6 summarizes the main conclusions and presents some suggestions for future investigation.
2. EVALUATION OF EFFICIENCY
The expression efficiencies or economies reflect any reduction, voluntary or involuntary, of the average cost of production recorded by an economic unit, which can be caused by multiple factors, among which one can distinguishes between the increase of production and technological progress. Efficiency gains in production are based on synergies on costs and reflect increases in economies of scale and scope. Economies of scale occur when the expansion of production capacity for one company or industry causes an increase in the total amount produced without a proportional increase in production cost. As a result, the average cost of the product tends to be lower with increased production since fixed costs or structure costs are distributed over a larger volume of production. Economies of scope consists on reductions in the total costs obtained by the production of multiple or complementary products. Scope economies are based on the principles of diversification and may promote competitive and strategic advantages.
The performance of a productive unit is often measured by productive efficiency indicators. The general concept of efficiency is related to how resources are used in the production process and can be decomposed into two components: technical efficiency and allocative efficiency. Technical efficiency is related to the evaluation of combinations of observed inputs/outputs compared to the best possible technological alternatives. Technical efficiency mainly reflects the efficiency of the production process to convert inputs into outputs. One company is considered technical efficient if, from a given set of inputs and available technology, it can produce as much output as possible (or for a given level of output and based on available technology, it can produce it with the least inputs). The evaluation of the allocative efficiency is associated with the best combinations of inputs to minimize production costs, given a certain price. One company is considered allocation efficient if it uses inputs according to the optimal structure that minimizes the production cost. One company is considered scale efficient (even if it is technical and allocation efficient) if it produces the amount of output that maximizes profit, that is, if its working at the optimal scale of production.
In the last few decades multiple methods for estimating efficiency have been developed, which can be classified into two main groups: parametric and nonparametric. Berger and Humphrey (1997) reviewed 130 empirical studies about efficiency in financial institutions from 21 countries and identify the most common used approaches: parametric (Stochastic Frontier Approach - SFA, Distribution Free Approach - DFA, Thick Frontier Approach - TFA) and nonparametric (Data Envelopment Analysis - DEA and Free Disposal Hull - FDH). The authors note that different methods do not produce consistent results. Also Berger et al. (1993) analyzed the results of several studies conducted by other researchers, which used SFA, TFA, DFA and DEA methods, and found that there is no rule defining which one is more appropriate to describe the true nature of financial institutions data. Moreover, they point the fact that the choice of the method and related variables significantly influences the efficiency levels results. Berger and Mester (1997) report that although efforts have been made in recent years for developing many empirical studies on the efficiency of the financial sector and banking, there is no consensus among researchers on the factors explaining the differences obtained in results, which may be in part explained by using different efficiency notions.
From all the studies about banking sector efficiency in Portugal, made on parametric methods, we highlight the work carried out by Mendes (1991), Mendes and Rebelo (1999; 2003), Pinho (1999; 2001) and Ribeiro (2006) and based on non-parametric methods (DEA), the work of Mendes (1994), Canhoto (1996; 1999), Canhoto and Dermine (2000), Camanho and Dyson (1999; 2005) and Portela and Thanassoulis (2007).
3. DATA ENVELOPMENT ANALYSIS (DEA)
According to Amado (2004) the first definition of technical efficiency has been developed by Koopmans (1951) and Debreu (1951) proposed the first measure of productive efficiency: the coefficient of resource utilization. These studies led Farrell (1957) to develop a methodology to calculate empirically the relative efficiency of different production units, allowing the decomposition of productive efficiency in technical efficiency and allocation efficiency. Charnes et al. (1978) developed the model proposed by Farrell (1957), converting the technical efficiency measure obtained by the initial model (based on a process of single input/output) to a process of multiple inputs/outputs.
Developed by Charnes et al. (1978) (1981) the methodology called Data Envelopment Analysis (DEA) is a linear programming mathematical technique, which converts multiple inputs and outputs in efficiency measures. The conversion is made by comparing the resources (inputs) used and the results (outputs) produced in each Decision Making Unit (DMU) with all other DMUs under study. The DMUs are organizational units with similar characteristics of any industry (manufacturing plants, schools, banks, hospitals, businesses, etc.). The application of DEA allows identifying the most efficient units in a population and, based on these provide a measure of inefficiency for the others, measuring the relative efficiency. The DEA models can be applied to minimize the inputs level to achieve a given level of output target (input oriented) or to maximize the output level to a particular fixed level of input (output oriented) (Thanassoulis, 2003).
Besides assessing the technical efficiency, DEA also evaluate the economies of scale present in the production process. Since the notion of economies of scale used in DEA methodology is quite similar to concepts in the classical literature on the theory of production, they are incorporated into the DEA methodology through different models. We can identify two main variants: CCR model, which considers the lack of a significant relationship between the operations scale and the efficiency level, assuming constant returns to scale, that is, the model assumes that an increase in output is proportional to the increase in inputs at any scale of production (Charnes, Cooper and Rhodes, 1978) and BCC model, which considers variable returns to scale and does not assume proportionality between inputs and outputs (Banker, Charnes and Cooper, 1984).
The study by Wang et al. (1997) about the impact of information technology on bank performance, introduced the two-stage concept in DEA. However, the authors applied traditional DEA models for each stage individually and subsequently analyzed, which they called for, the overall efficiency using a model with the inputs of stage 1 and the outputs of stage 2, ignoring the existence of intermediate measures. Others authors have followed their example (Seiford and Zhu, 1999) (Lo and Lu, 2006). Studies made under this type of individual approach to sub-independent models, allow inefficient DMUs considered in one (or both) of the models of each step, fall efficient overall. This reflects the inability of traditional DEA models to evaluate the performance in the presence of two stages processes, and therefore inter-dependent, characterized by the existence of intermediate measures.
The actual two-stage models assumes that the production process is composed of sub-processes (or stages) and has the particularity to use the outputs from the model of stage 1 as unique inputs of the model of stage 2. Variables common to both models are called, in this context, intermediate measures. Chen and Zhu (2004) develop the study of Wang et al. (1997) starting from the presuppositions that (in)efficiency of a stage influence the (in)efficiency of the other because of the existence of common intermediate measures. In this context, authors derive the two-stage model under the assumption of variable returns to scale, using the following linear programming problem:
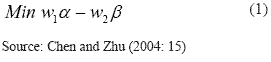

In this model the variables w1 and w2 correspond to the weights assigned to each stage and the symbol ~ represents an unknown decision variable. The two-stage model aimed at minimizing the use of resources to maximize the output. Thus, in stage 1 the model is input oriented and in stage 2 is output oriented, considering both the existence of an intermediate decision measure. If α* = β* = 1 then there should be an optimal solution in which where the symbol * represents the optimum value in the model. In this case, the two stages achieve efficiency and the two-stage process is considered as a single or global process. Note that in this case the values match the efficiency levels achieved in traditional DEA models. If α* = 1 and β*> 1 (or α* < 1 and β* = 1) then the model shows that one stage can achieve 100% efficiency, through the existence of a set of optimal intermediate values. It also permits the determination of the optimum values for the intermediate variable to achieve efficiency in both stages.
Kao and Hwang (2008) modify the CCR traditional DEA model incorporating a set of relations between the two stages and demonstrate that the overall efficiency level (Ek) from the two-stage model calculated as the product between the efficiency levels of the two stages, is a most appropriate indicator that the one calculated according to the concept of Wang et al. (1997). Chen et al. (2009c) demonstrate that the model of Kao and Hwang (2008) is equivalent to the model of Chen and Zhu (2004) under the assumption of constant returns to scale (CCR). Thus, Chen and Zhu (2004) two-stage model determines the overall efficiency levels but only under the assumption of constant returns to scale, where α* = 1 and β* = overall efficiency index.
Chen et al. (2009a) reported that the model of Kao and Hwang (2008), besides assuming constant returns to scale, assume equal weights for the two stages. The authors circumvent this limitation of the model by creating an additive approach that allows both the assumption of constant returns to scale and variable return to scale. The additive approach assumes that the overall efficiency of the two-stage model is a weighted sum of the efficiencies of individual stages. Chen et al. (2009b) reported that the overall performance indicators discussed above are not sufficient to project the inefficient DMUs to the efficient frontier, since they do not identify, in a direct manner, the necessary reductions to inputs (or increases in outputs) to achieve efficiency, such as in traditional DEA models. In other words, these studies determine an overall efficiency measure, but do not determine the efficiency frontier for the two-stage model. The authors develop an alternative two-stage model that allows the projection of inefficient DMUs to the efficient frontier, but only under the assumption of constant returns to scale. It is still under investigation the correspondent adaptation to variable returns to scale.
4. METHODOLOGY
Financial data from the year 2007 of 37 banks operating in Portugal was selected. Data was collected from the Annual Reports and Accounts of the banks and Newsletters of the Portuguese Association of Banks. Extra-accounting information was also collected, in particular, the rating assigned by the worldwide financial consultants (Standard & Poors, Moodys and Fitch).
Whereas the DEA provides an efficiency analysis in relative terms, it is important to ensure DMUs homogeneity in the sample under study. In this context, to obtain relatively homogeneous groups, the initial sample was divided into two, based on the size/business and risk factors. The sample in Group 1 includes 18 large banks (number of branches > 15) and sample in Group 2 includes the remaining 19 smaller banks, specialized in certain market segments or business areas. From the initial sample, another two groups of banks were created under a risk factor, evaluated on solvency and long-term rating assigned by the main financial consultants. Group 3 includes 17 banks with the lowest risk index and Group 4 the remaining 20 banks with higher risk.
A careful selection of input/output variables for inclusion in the DEA model is particularly relevant in the banking sector, since two major approaches coexist, associated to the main type of activity inherent to the business: the intermediation approach where banks are regarded as financial intermediaries whose primary business is the gathering of resources from savers (savings/deposits) and the mobilization of these funds to others for investment activities in the form of loans, by carrying out an income (interest, commissions, etc. ..); and the production approach where banks are considered institutions that use capital and labor to provide services, or to provide loans and manage deposits. In this context, the main problem surrounds the deposits classification, since in the intermediation approach deposits are considered inputs and in the production approach are considered outputs.
Several authors mention the need to incorporate in the banks evaluation performance models, variables that reflect, besides profitability, value creation, risk and opportunity costs for shareholders (Fiordelisi and Molyneux, 2004; 2006) (Tabak et al., 2005). The variable value created for shareholders, which corresponds to the intrinsic value added, was calculated from the equity perspective, based on the concept of Tabak et al. (2005). For the calculation of the value creation measures, it was necessary to estimate a proxy variable for the cost of equity due to the lack of published information on it. The latter was estimated based on the real rate of return on risk-free assets, the average annual rate of inflation and the risk premium associated with the bank (estimated based on the rating assigned by the major world financial consultants).
The main model used in this study evaluates the efficiency of banks trough Chen and Zhu (2004) two-stage model, based on two sub-models: Production and Intermediation Model as stated in figure 1. This model was created based on the main schedule of Seiford and Zhu (1999) and on the concept of the intermediate revisionist vision approach referenced by Pinho (1995). This kind of model assesses the significance of intermediate measure (Deposit), main connector among savers and investors, and permits simultaneously to circumvent the problem associated to the choice of one main approach.
Figure 1 - Two-stage Model of Production/Intermediation applied in the study
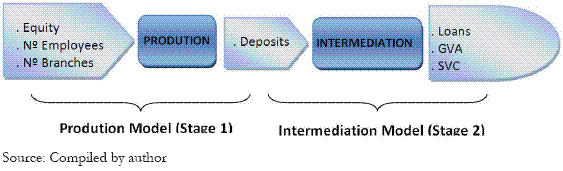
The Production Model incorporates as input variables equity, number of employees and number of branches and as output variable the deposits. The Intermediation Model incorporates as input variable deposits and as output variables loans, gross value added and shareholder value created. To complement these approaches the Profitability Model evaluates the bank ability to create results from the income generators and the available structure. For this model was used as input variables the cost of structure and liquid financial assets and as outputs the interest margin and net operating income.
Relatively to the nature of returns to scale, the possibility of variable returns to scale was considered as a more consistent alternative. Most of the empirical studies record variable returns to scale in the banking sector (Mendes, 1991; 1994) (Mendes and Rebelo, 1999; 2003) (Canhoto, 1996; 1999) (Camanho and Dyson, 1999; 2005) (Pinho, 1999; 2001) (Seiford and Zhu, 1999) (Camanho and Dermine, 2000) (Lo and Lu, 2006) (Ribeiro, 2006) (Portela and Thanassoulis, 2007).
All results of DEA models were obtained through the specific DEAFrontier software (Zhu, 2009) which is a supplement to the Excel solver. The statistic test results were obtained through the statistical SPSS (Statistical Package for Social Sciences) software.
5. MAIN RESULTS
Table 1 summarizes the statistical results obtained by the traditional DEA models. We highlight the following facts: the profitability model notes higher average efficiency indicators and lower standard deviation measures; the intermediation model notes lower average efficiency measures and higher standard deviation measures; in 8 of 12 cases the standard deviation of efficiency decreases as we divide the whole group in smaller and more homogeneous ones; in 9 of 12 cases the average efficiency increases when we divide the whole group in smaller and more homogeneous ones.
Table 1 - Summary Statistics of Traditional DEA Models
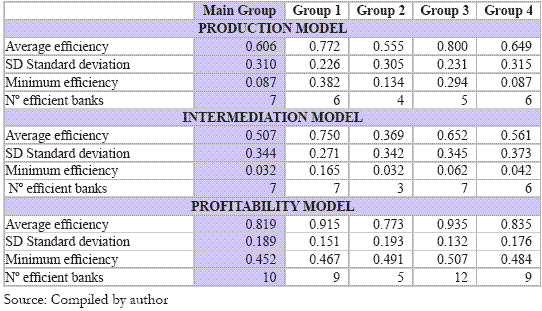
Differences among efficiency levels from the traditional DEA models were analyzed based on the nonparametric Friedman test, since the requirement for normality failed. The significance of the Friedman test (0,000) rejects the hypothesis of equality in the central tendency of distributions of the various models efficiencies, for a confidence level of 95%. The efficiencies of different models are considered to be statistically different, with the profitability model presenting the highest efficiency levels and the intermediation model the lowest.
We analyzed the type of return to scale for each bank in each model. For inefficient banks features of return to scale are related to their projection on the efficient frontier. The results differ greatly among models. While in the production model most (56.8%) of banks present increasing returns to scale, the same number of banks present decreasing returns to scale in the profitability model. The intermediate model present 94.6% of banks with features of decreasing returns to scale, not recording any bank with increasing returns. There are many banks with variable returns to scale in all models, which explain, in part, the choice of DEA BCC model. In the production and profitability models, most of the larger banks (group 1) have decreasing returns to scale, while most of the smaller banks (group 2) have increasing returns to scale.
The production model has an average efficiency of 60.6%. Since the model is input oriented, we can conclude that, on average, banks could produce the same level of output with less 39.4% of resources. Intermediation model has an average efficiency of 50.7%. Since the model is output orientated, we can conclude that, on average, banks could produce more 49.3% of results with the same level of deposits. The profitability model obtained the highest efficiency level of 81.9%.
Many models present technologically efficient banks that are not operating on the most efficient production scale, achieving very low overall efficiency levels. On the other hand, there are other banks with high scale efficiency scores, but also with high inefficiencies in managing its resources.
Figure 2 crosses the efficiency levels achieved in traditional DEA models, according to the production and the intermediation approaches. The markers are discriminated by the value creation for shareholders levels, based on the variable Economic Value Added (EVA1). It seems that banks which raise the highest levels2 of value creation (level 4: EVA > 25,001 m) obtained good levels of production efficiency (case of Banco BPI) or intermediation efficiency (case of BST and BCPI) or both (case of CGD). Banks such as BES or BCP, although with good efficiency levels, present the lowest levels of value creation for shareholders. The vast majority of banks with low efficiency levels also have lower level of value creation. The significance of Kruskal-Wallis test showed that banks with higher value creation also have higher levels of intermediation efficiencies.
Figure 2 - Efficiencies Matrix of Production vs. Intermediation Models
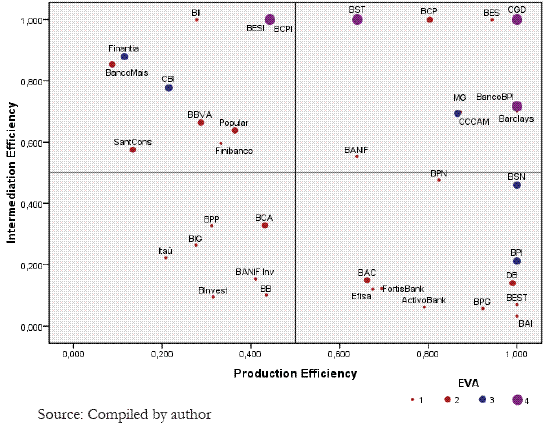
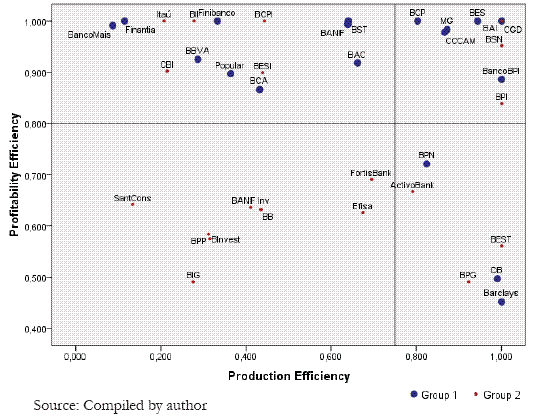
Figure 3 crosses the efficiency levels achieved in traditional DEA models, according to the production and the profitability approaches. The markers are discriminated according to the size/business factor by groups as defined previously. We can see that 7 of 9 banks with the highest efficiency levels (upper right quadrant) belong also to group 1 (larger banks). Most of the smaller banks (group 2) obtained simultaneously low production and profitability efficiency levels. Small banks such as BSN or BPI have good production and profitability efficiency levels. The significance of Mann-Whitney test shows that larger banks have higher profitability efficiency levels.
Figure 3 - Efficiencies Matrix of Production vs. Profi tability Models
The Two-stage Model of Production/Intermediation
Efficiency Analysis of the Total Group: The two-stage model (1) proposed by Chen and Zhu (2004) has been carried out using the Production/Intermediation approach under the assumption of variable returns to scale (BCC), trough DEAFrontier software.
They were identified 25 banks which achieve the maximum efficiency level (100%) in stage 1 (production) but are inefficient in terms of intermediation, while only 4 banks obtain maximum efficiency in stage 2 (intermediation) but are inefficient in terms of production. Only CGD get maximum efficiency in the two stages. The other 7 banks are not efficient in any of the stages. Thus, it seems that, according to the two-stage model 70.3% (26 of 37) of the banks are efficient in terms of production and only 13.5% (5 of 37) are efficient in terms of intermediation.
Table 2 summarizes the results obtained by the two-stage model. The fourth column (optimal DEP) refers to the optimal level found by the model for the intermediate variable (deposits) that allows the maximization of the efficiency levels. The last column shows the change required to each bank in order to achieve the optimal level of deposits, given the level recorded. Efficient banks in stage 1 such as BAI, BEST, BPI, Banco BPI and CGD and BCP, BES, CGD and BST efficient in stage 2 are already on the optimal level of deposits to maximize their efficiency levels according to a perspective of two-stages.
Table 2 - Two-stage Model Results
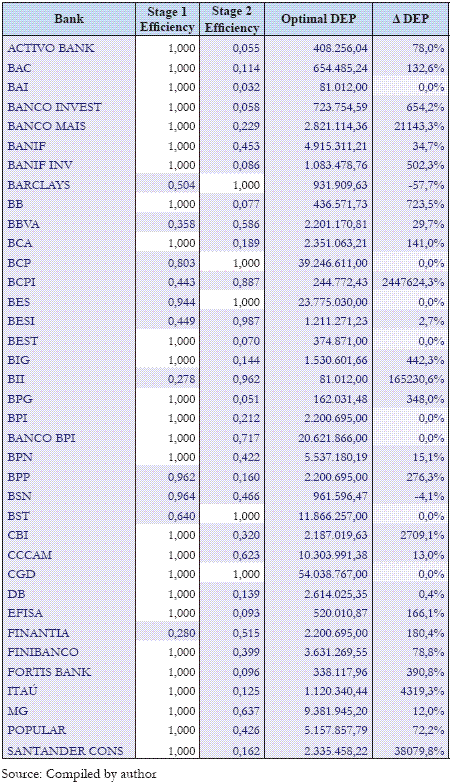
Several banks (such as DB, BESI, MG, CCCAM and BPN) can, with some effort to adopt strategic measures, achieve or at least approach the optimal value of deposits. For most banks the model values are mathematically possible, but probably difficult, even impossible, to achieve considering its mission or business area. For example, banks such as BCPI, BII, Santander Consumer or Banco Mais are very far from being able to achieve efficiency, since their business area does not promote the collection of deposits as a primary objective. These are precisely the banks with the lowest intermediate variable values.
Efficiency Analysis by Groups: The efficiency levels achieved in the global frontier for each stage of the two-stage model were discriminated by a size/business factor (group 1 and 2) and risk (group 3 and 4). Differences were evaluated using the non-parametric Mann-Whitney test. The hypothesis H0 of equality in the central tendency of the efficiency levels distributions for the various groups was tested for a confidence level of 95%. There is no evidence of differences between the efficiency levels in stage 1 for the banks belong with group 1 and 2 (sig. 0,707). For stage 2, the efficiency levels of groups 1 and 2 are considered statistically different (sig. 0,001), with group 1 (larger banks) achieving higher efficiency levels. There is no evidence of differences between the efficiency levels in stage 1 for the banks belong with group 3 and 4 (sig. 0,557). For stage 2, efficiency levels of groups 3 and 4 are considered to be statistically different (sig. 0,012), with group 3 (lower risk banks) achieving higher efficiency levels.
To evaluate the relationship between the two-stage model efficiency levels and value creation, the nonparametric Kruskal-Wallis test was applied. The efficiency levels achieved in the two-stage model were discriminated by a value creation factor, according to two variables (Economic Value Added: EVA and Intrinsic Value Added: IVA3). The tests do not reject the hypothesis of equality in stage 1 (EVA sig. 0,436; IVA sig. 0,202). However, the efficiency levels of stage 2 for the banks with different value creation levels are statistically different (EVA sig. 0,014; IVA sig. 0,000), since banks with higher value creation present higher efficiency levels.
To evaluate the affect of sample homogeneity on efficiency levels, efficiency levels achieved in the global frontier were compared with efficiency levels obtained at the frontier of each group through the nonparametric Kruskal-Wallis test. Efficiencies of the various groups are considered statistically different, with group 3 (lower risk banks) in stage 1 and group 1 (larger banks) in stage 2 achieving higher efficiency levels.
For each factor in study, the difference among efficiency levels of groups 1 vs. 2 and 3 vs. 4 was evaluated, using the non-parametric Mann-Whitney test. Efficiency levels between group 1 and 2 are considered statistically different, with group 1 (larger banks) achieving higher levels of production (sig. 0,001) and intermediation (sig. 0,003) efficiencies. There is no evidence of differences between efficiency levels of group 3 and 4, i.e., the risk factor seems to have no influence in establishing levels of production (sig. 0,257) and intermediation (sig. 0,537) efficiency.
Comparative Analysis between Two-stage Model and Traditional Models: A comparative analysis between the results obtained in traditional DEA models (Production and Intermediation Models), the Global Model (composed with the inputs of the production model and the outputs of the intermediation model) and the Two-stage Model was performed.
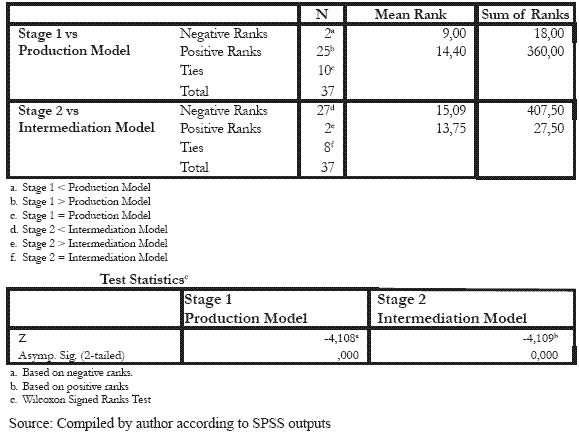
The global model ranks as efficient 12 banks that are inefficient in one traditional model (production or intermediation) and ranks as efficient 5 banks that are inefficient in both traditional models (production and intermediation). The only bank classified as efficient in all models is CGD. Several banks classified as efficient in the global model, get very low efficiency levels in the two-stage model (examples: BII, BCPI, BESI, Barclays, BAI, BEST, Efisa and Fortis Bank). The difference between efficiency levels achieved in the traditional production and intermediation models and efficiencies levels of stages 1 and 2 of the two-stage model was analyzed trough the non-parametric Wilcoxon test (paired samples). The results are resumed in Table 3. The hypothesis of equal efficiency levels achieved by the various models, for a confidence level of 95% was tested. The efficiencies of different models are considered to be statistically different, since efficiency level obtained in stage 1 in the two-stage model is higher than the levels obtained in the production model for 25 banks, and the efficiency levels in stage 2 are lower than the levels obtained in the intermediation model in 27 cases.
Table 3 - Wilcoxon Signed Ranks Test to Two-stage vs. Traditional Model
Several authors cross the results obtained among models, or between them and financial variables, according to a matrix similar to the BCG Matrix (Boston Consulting Group), to outline possible strategies to promote increased efficiency (Boussofiane et al., 1991) (Camanho and Dyson, 1999) (Lo and Lu, 2006).
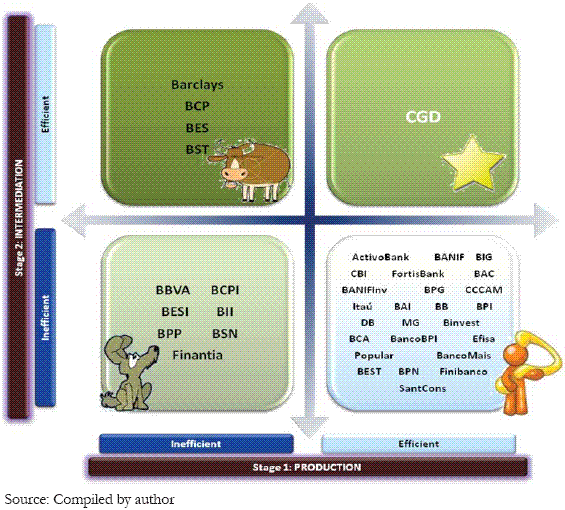
For the two-stage approach in terms of production/intermediation followed in this study, we propose the following adjustment to the BCG matrix: the strategic variables from the BCG matrix correspond to the efficiency levels achieved in the production model (stage 1) and in the intermediation model (stage 2). Each of them is divided into two quadrants: efficient vs. inefficient. Crossing the strategic variables will result four quadrants that represent the bank position and what strategy is needed to improve overall efficiency. The quadrants are as follow:
Question marks: represent the banks that are production efficient but are inefficient transforming resources into results. Since they have a good ability to manage their inputs they should emphasize measures to improve its ability to maximize outputs. The strategy is to achieve the Star quadrant by increasing the intermediation efficiency otherwise there is the risk to become into the Dogs quadrant.
Star: represent the banks that are production and intermediate efficient. They should follow strategies to maintain its efficiency. Generally, these banks represent units of good practices, which are considered benchmarks for others.
Cow: represent the banks that are intermediation efficient but are inefficient in managing their resources. Since they have a good capacity for create results, they should emphasize measures to improve its ability to minimize inputs. The strategy is to achieve the Star quadrant by increasing production efficiency otherwise there is the risk to become into the Dogs quadrant.
Dogs: represent the banks that are inefficient in terms of production and intermediation. These banks must rethink their strategy at various levels to promote the use of available resources.
The only bank positioned in the Star quadrant is CGD, becoming the most efficient bank. However, CGD is not the bank with the largest number of references to their peers (peer group). In stage 1 is referenced in only 13% of the cases and is largely exceeded by BPI (37%) or even by BAI (18%); in stage 2 the only reference that present is for itself. Furthermore, the analysis carried out for all the traditional DEA models independently show that the high efficiency results obtained by CGD can be false, as it also get the maximum level of inefficiency in the inverted frontier and a low compound efficiency4. In this case, although efficient, CGD does not seem to be a typical example of a good practice unit to be followed by others. It is necessary to apply an extra DEA further investigation to evaluate the hypothesis if CGD is whether or not an efficient bank or efficient by default5, as it presents the highest values of the sample, for all the variables included in the models.
The banks BCP, BES, BST and Barclays are positioned in the Cow quadrant. These banks are efficient creating results, but inefficient managing its resources. Implementing measures to improve its production efficiency would simplify their rise to the Star quadrant. The banks BBVA, BCPI, BESI, BII, BPP, BSN and Finantia are positioned in the Dogs quadrant. These banks are production and intermediation inefficient and should rethink their strategy at various levels to promote the use of available resources. The remaining 25 banks (67.6%) are positioned in the Question Marks quadrant since they are only production efficient. These banks have a high potential to progress in terms of efficiency to achieve the Star quadrant. It is necessary to concentrate efforts to maximize their results.
Figure 4 : Adjusting the BCG Matrix to the Two-stage Model
6. CONCLUSIONS AND SUGGESTIONS FOR FUTURE RESEARCH
When analyzing the results obtained by DEA traditional models at an independent basis, the model that shows the highest average efficiency level is the profitability model (81.9%) and the lowest average efficiency levels the intermediation model (50.7%). There are many banks with variable returns to scale in all models, which justify, in part, the choice of BCC DEA model. In the production and profitability models most large banks experience decreasing returns to scale, while most of the smaller banks experience increasing returns to scale. These results are consistent with the results of Canhoto (1996), Seiford and Zhu (1999) and Lo and Lu (2006). Many models present technological efficient bank not operating on the most efficient scale of production, achieving very low overall efficiency levels. The pure technical efficiency average is generally higher than the global efficiency, revealing the existence of scale inefficiencies in many banks. M&A transactions may lead to potential increases in efficiency in these cases. On the other hand, there are banks with high scale efficiency but with high inefficiencies managing its resources. Overall, we conclude that most banks have very low efficiency levels, which reflects the need for a major effort to improve the use of resources. It also seems that banks with higher value creation have higher intermediation efficiencies and that larger banks have higher profitability efficiency levels.
When applying the two-stage model and analyzing the entire sample, the size/business factor seems to have no influence on the production efficiency levels, but influence on intermediation efficiency, in which the bigger banks present higher intermediation efficiency. The same is true for the risk and value creation factor: banks with higher intermediation efficiency correspond to banks with lower risk and greater value creation. However, when comparing the efficiency levels among groups the size/business factor has influence on both efficiency levels and the risk factor does not influence any of them. These results are similar when analyzing traditional DEA models independently. Dividing the main sample into more homogeneous groups does influence the efficiency levels. The size/business factor seems to influence the intermediation efficiency and the risk factor the production efficiency. Comparing results from the two-stage model with the traditional DEA models, we confirm the findings of other studies which classify as global efficient some inefficient DMUs in one (or both) models that composed each stage. This reflects the inability of traditional DEA models to evaluate the performance in the presence of two-stage processes, and therefore inter-dependent, characterized by the existence of intermediate measures. There is evidence that the use of the two-stage model, i.e., considering the existence of intermediate measures, influence the determination of efficiency levels.
There is a need to supplement this study with an extra DEA analysis to better understand the results. Moreover, the application of a Tobit regression can help identify the variables with greatest influence on performance indicators. Additional studies that might prove to be useful would be the inclusion of weight restrictions (in the variables and/or stages) and new variables related to technology, quality or not controllable by managers. We intend to continue this study to evaluate the impact of M&A transactions in the performance indicators trough the two-stage model and to apply it to a single bank to conduct the study at branch level.
ENDNOTES
1- Calculated according to the equity perspective as suggested by Fiordelisi and Molyneux (2004) and Carretta et al. (2008) and according to the formula proposed by Young and OByrne (2001):
EVAn = Equityn-1 (rn - kn), with rn: return on equity and kn: proxy of cost of equity
2- The following levels were created: level 1 (EVA < 0); level 2 (1 < EVA < 10.000); level 3 (10.001 < EVA < 25.000); level 4 (EVA > 25.001).
3- The following levels were created: level 1 (IVA < 0); level 2 (1 < IVA < 50.000); level 3 (50.001 < IVA < 250.000); level 4 (250.001 < IVA < 1.000.000); level 5 (IVA > 1.000.001).
4- Since the standard efficient frontier represents an optimistic approach and the inverted frontier a pessimistic one, we can determine the compound level of efficiency that encompasses these two aspects, calculating the arithmetic mean between both. Thus, the level of compound efficiency requires an efficient DMU to achieve good performance in the areas where it is better (high standard efficiency) and to achieve an acceptable performance in areas where it is worse (low inverted efficiency).
5- The mathematical properties of BCC model allows the DMUs with the lowest value of one input (or the highest value of one output) are considered efficient, even if the other variables do not exhibit the best relationships (Ali, 1993).
REFERENCES
ALI, Agha Iqbal (1993): Streamlined computation for Data Envelopment Analysis, European Journal of Operational Research, 64, pp. 61-67.
AMADO, Carla A. F. (2004): Exploring the use of DEA for formative evaluation in primary care: an application to England, Estudos I, Universidade do Algarve, Faculdade de Economia, pp. 563-596.
BANKER, Rajiv D.; CHARNES; COOPER (1984): Some models for estimating technical and scale inefficiencies in data envelopment analysis, Management Science, 30, (9), pp. 1078-1098.
BERGER, Allen N.; HUMPHREY (1997): Efficiency of financial institutions: international survey and directions for future research, European Journal of Operational Research, 98, pp. 175-212.
BERGER, Allen N.; HUNTER; TIMME (1993): The efficiency of financial institutions: a review and preview of research past, present, and future, Journal of Banking & Finance, 17, pp. 221-249.
BERGER, Allen N.; MESTER (1997): Inside the Black Box: What explains differences in the efficiencies of financial institutions?, Financial Institutions Center, The Wharton School, University of Pennsylvania, Working Paper n.º 04.
BOUSSOFIANE, A.; DYSON; THANASSOULIS (1991): Applied Data Envelopment Analysis, European Journal of Operational Research, 52, pp. 1-15.
CAMANHO, A. S.; DYSON (2005): Cost efficiency measurement with price uncertainty: a DEA application to bank branch assessments, European Journal of Operational Research, 161, (2), pp. 432-446.
CAMANHO, A. S.; DYSON (1999): Efficiency, size, benchmarks and targets for bank branches: an application of data envelopment analysis, Journal of the Operational Research Society, 50, pp. 903-915.
CANHOTO, Ana Maria (1999): Efficiency and competition in portuguese banking: an empirical investigation, PhD Dissertation in Economics, Universidade Católica Portuguesa, Faculdade de Ciências Económicas e Empresariais.
CANHOTO, Ana Maria (1996): Technical efficiency in the Portuguese Banking Sector: a non-parametric approach, Universidade Católica Portuguesa, Working Paper n.º 71.96, Março.
CANHOTO, Ana Maria; DERMINE (2000): A non-parametric evaluation of banking efficiency in Portugal: new vs. old banks, The European Institute of Business Administration, INSEAD WP 2000/03/FIN.
CARRETTA, Alessandro; FARINA; FIORDELISI; SCHWIZER (2008): Corporate culture and shareholder value in banking industry, Munich Personal RePEc Archive, MPRA Paper No. 8304.
CHARNES A.; COOPER; RHODES (1981): Evaluating program and managerial efficiency: an application of Data Envelopment Analysis to program follow through, Management Science, 27, (6), pp. 668-697.
CHARNES, A.; COOPER; RHODES (1978): Measuring the efficiency of decision making units, European Journal of Operational Research, 2, pp. 429-444.
CHEN, Yao; COOK; LI; ZHU (2009a): Additive efficiency decomposition in two-stage DEA, European Journal of Operational Research, 196, (3), pp. 1170-1176.
CHEN, Yao; COOK; ZHU (2009b): Deriving the DEA frontier for two-stage processes, European Journal of Operational Research, in press, doi: 10.1016/j.ejor.2009.05012.
CHEN, Yao; LIANG; ZHU (2009c): Equivalence in two-stage DEA approaches, European Journal of Operational Research, 193, (2), pp. 600-604.
CHEN, Yao; ZHU (2004): Measuring Information Technologys indirect impact on firm performance, Information Technology and Management, 5, (1-2), pp. 9-22.
DEBREU, G. (1951): The coefficient of resource allocation, in Econometrica, 19, (3), pp. 273-292. [ Links ]
EMROUZNEJAD, Ali; THANASSOULIS (2001): An Extensive Bibliography of Data Envelopment Analysis (DEA): Volume I to V, Business School, University of Warwick, England.
FARRELL, M. J. (1957): The measurement of productive efficiency, Journal of the Royal Statistical Society, 120, pp. 253-281.
FIORDELISI, Franco; MOLYNEUX (2006): Do cost and profit efficiency drive shareholder value? Evidence from European banking, Financial Management Association International European Conference - Stockholm, June.
FIORDELISI, Franco; MOLYNEUX (2004): Measuring Shareholder value in European banking, University of Wales, Bangor Business School, Working Papers.
KAO, Chiang; HWANG (2008): Efficiency decomposition in two-stage Data Envelopment Analysis: an application to non-life insurance companies in Taiwan, European Journal of Operational Research, 185, (1), pp. 418-429.
KOOPMANS, T. (1951): An analysis of production as an efficient combination of activities, Activity Analysis of Production and Allocation, Cowles Commission for Research in Economics, Monograph 13, New York, Wiley.
LO, Shih-Fang; LU (2006): Does size matter? Finding the profitability and marketability benchmark of financial holding companies, Asia-Pacific Journal of Operational Research, 23, (2), pp. 229-246.
MENDES, Victor (1994): Eficiência Produtiva no Sector Bancário: uma aplicação do método DEA aos anos 1990-92, Investigação – Trabalhos em Curso, Economia, n.º 42, Faculdade de Economia, Universidade do Porto. [ Links ]
MENDES, Victor (1991): Scale and scope economies in Portuguese commercial banking: the years 1965-88, Economia, XV, (3), pp. 453-490. [ Links ]
MENDES, Victor; REBELO (2003): Structure and performance in the Portuguese banking industry in the nineties, Portuguese Economic Journal, 2, pp. 53-68. [ Links ]
MENDES, Victor; REBELO (1999): Productive efficiency, technological change and productivity in Portuguese banking, Applied Financial Economics, 9, pp. 513-521.
PINHO, Paulo Soares (2001): Using accounting data to measure efficiency in banking: an application to Portugal, Applied Financial Economics, 11, pp. 527-538.
PINHO, Paulo Soares (1999): Reprivatizações e eficiência no sistema bancário português, Ministério das Finanças e da Administração Pública, Direcção-Geral de Estudos e Previsão, Documento de Trabalho n.º 13, Setembro.
PINHO, Paulo Soares (1995): Economias de escala e eficiência produtiva na banca portuguesa – uma revisão da literatura, Faculdade de Economia da Universidade Nova de Lisboa, Working Paper nº. 241, Janeiro.
PORTELA, Maria Conceição A. Silva; THANASSOULIS (2007): Comparative efficiency analysis of Portuguese bank branches, European Journal of Operational Research, 177, pp. 1275-1288.
RIBEIRO, Maria Clara Dias Pinto (2006): Economia de escala e de gama e os efeitos da concentração na eficiência bancária, PhD Dissertation, Biblioteca da Universidade do Minho, ref. 1822/6098.
SEIFORD, Lawrence M.; ZHU (1999): Profitability and marketability of the top 55 US commercial banks, Management Science, 45, (9), pp. 1270-1288.
TABAK, Benjamin Miranda; KRAUSE; PORTELLA (2005): Eficiência bancária: o valor intrínseco na função de produção, Revista de Administração, Universidade de São Paulo, Brasil, 40, (4), pp. 361-379.
THANASSOULIS, Emmanuel (2003): Introduction to the Theory and Application of Data Envelopment Analysis: a foundation text with integrated software, 2nd Edition, Kluwer Academic Publishers.
WANG, Chien H.; GOPAL; ZIONTS (1997): Use of DEA in assessing Information Technology impact on firm performance, Annals of Operations Research, 73, pp. 191-213.
YOUNG, David; OBYRNE (2001): EVA and Value-Based Management – A practical guide to implementation, McGraw-Hill.
ZHU, Joe (2009): Quantitative Models for Performance Evaluation and Benchmarking – Data Envelopment Analysis with Spreadsheets, 2nd Edition, Springer.
Recebido: 23.09.2009 - Aceite: 15.12.2009