Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Motricidade
Print version ISSN 1646-107X
Motri. vol.15 no.1 Ribeira de Pena Mar. 2019
https://doi.org/10.6063/motricidade.16370
ARTIGOS ORIGINAIS
Data-driven analysis of point-by-point performance for male tennis player in Grand Slams
Yixiong Cui1, Haoyang Liu1[*], Hongyou Liu2,3, Miguel-Ángel Gómez4
1AI Sports Engineering Lab, School of Sports Engineering, Beijing Sport University, Beijing, China
2School of Physical Education & Sports Science, South China Normal University, Guangzhou, China
3National Demonstration Centre for Experimental Sports Science Education, South China Normal University, Guangzhou, China
4Facultad de Ciencias de la Actividad Física y del Deporte, Universidad Politécnica de Madrid, Madrid, Spain
ABSTRACT
Tennis is an individual sport that requires a specialized training and match preparation for every player. Former studies in tennis have tried many approaches to analyze players performance using descriptive statistics (such as: match time, rally duration, or game number) and match-related statistics (such as: first and second serve percentage, aces, double faults, or net points won). Although helpful in providing general information of match characteristics and evaluating player performance, there is scarce consideration over how elite male players behave on point-by-point basis according to different contextual variables. This study aimed to assess predictors of point outcome (win/lose) related to year, tournament types, round, set, quality of opposition, game status, serve and rally by using match data of 2011-2016 four Grand Slam. A total of 29675 points were recorded and analyzed through classification tree analysis (exhaustive CHAID). The results showed that the performance of tennis player was conditioned by the familiarity with court surfaces as well as other contextual variables, such as game type, quality of opposition, match status, serve and return and rally length (p< 0.05). These results provide insight for coaches and players when planning the game strategy, allowing more appropriate tactics under different game status.
Keywords: racket sports; performance analysis; training; contextual variables; data analysis.
INTRODUCTION
Match performance of tennis player is one of the topics that attract major research interest in sport performance analysis (McGarry, O’Donoghue, & Sampaio, 2013). Competing in professional tennis requires player to win the game by making proper strategies and tactics according to different tournaments, rounds, sets, quality of opponents and consistently tailoring them based on the match periods and match status. With the application of performance profiling techniques, the technical, tactical, physical and psychological features of tennis players could be evaluated and compared (Butterworth, O’Donoghue, & Cropley, 2013). The available research has intended to describe the performance of tennis players of different sex (Hizan, Whipp, & Reid, 2011) and different levels (Galé-Ansodi, Castellano, & Usabiaga, 2016; Sanchez-Pay, Palao, Torres-Luque, & Sanz- Rivas, 2015), considering the match outcome or game location (McGarry et al., 2013; Reid, Morgan, & Whiteside, 2016). However, little was known about how the performance of a tennis player is influenced by other contextual factors, such as the opponents quality and match status, which have been investigated in major team sports like basketball and football (Gómez, Lorenzo, Ibañez, & Sampaio, 2013; Lago-Peñas, 2012). These contextual factors take into consideration the game location, game status, quality of opposition, period of play and type of competition and their effects on players performance and game outcome (Gómez, Lago, & Pollard, 2013).
Gillet, Leroy, Thouvarecq, and Stein (2009) were ones of the first to assess the influence of game location on tennis players serve and return performance, after which Galé-Ansodi et al. (2016) attempted to describe the physical performance of youth tennis player on hard and clay courts. More recently Reid et al. (2016) described the match performance of male and female tennis players in Australian Open, which was on hard court. However, the influence of other court surface like grass, strength of the opponents and game status were not considered. Hence, it is of interest to know how tennis player perform under these different contextual circumstances.
As the application of new technology in sport fields is generating a great amount of data on match and training performance of athletes (Hughes & Franks, 2015; McGarry et al., 2013), it is necessary to evaluate their performance in a more in-depth manner for advanced understanding of match behaviors. This ultimately can be used to help in-game coach decision-making with emphasis on those performance indicators which are of greatest relevance to achieving a winning outcome and also to optimizing individualized training for players (Reid, McMurtrie, & Crespo, 2010; Reid et al., 2016).
Applying data mining and statistical modelling techniques, sport data could be interpreted to provide meaningful information and insights (Ofoghi, Zeleznikow, MacMahon, & Raab, 2013). And being one of these techniques, classification tree analysis has been used lately by researchers of sport science, particularly in team sports (Gómez, Battaglia, et al., 2015) and proved to be useful in modeling non-linear phenomena. It establishes a hierarchical solution to classify complex problems, where a set of rules is derived from the interaction between attributes in a data set, with high predictive accuracy (Gómez, Battaglia, et al., 2015). Previous studies has applied the technique to model the ball screen effectiveness in basketball (Gómez, Lorenzo, et al., 2013), the match outcome in Australian football (Robertson, Back, & Bartlett, 2016), the ball possession effectiveness in futsal (Gómez, Moral, & Lago-Peñas, 2015) and the effect of scoring first on match outcome in football (Lago- Peñas, Gómez-Ruano, Megías-Navarro, & Pollard, 2016). This inspired us to use this model to analyze in detail how tennis player performed when competing against various level of opponents under distinct match status on different court surfaces and understand their interactions, instead of just analyzing and comparing the result of the performance.
Therefore, by applying the classification tree model, the present study was aimed to examine the point-by-point performance of tennis players in four Grand Slams, considering comprehensively various contextual variables such as court surfaces, opponents quality and match status. According to the existing knowledge and variables included in the study, it is hypothesized that players would exhibit better performance when competing against lower- ranked opponents or have positive match status such as winning in his service or return game. Meanwhile, we expect that players would perform worse when playing in the quarterfinals, semifinals and finals as well as playing longer rally points.
METHOD
Participants
Point-level data of 145 Grand Slam main-draw mens singles matches played by a top ranked male tennis player and his opponents within year 2011 to 2016 were collected from separate official tournament websites: Australian Open (www.ausopen.com), Roland Garros (www.rolandgarros.com), Wimbledon (http://www.wimbledon.com) and US Open (www.usopen.org). The player was stably ranked top 3 in Association of Tennis Professionals (ATP, www.atpworldtour.com) through 2011-2016, being number 1 in ranking from 2014-2016. Therefore, the analysis of this player and his opponents is not only expected to guarantee a better understanding on how elite tennis players are conditioned by matches contexts but also and provides point-level performance profiles of those players.
The data included the notational statistics such as first and second serve, rally numbers and game scores; and ball speed statistics collected by Doppler radar system (IBM: Armonk, NY, USA) that were installed in the courts. Matches that were not completed due to the retirement of the opponents or a walkover were excluded from the study. In total, there were 29675 points (8035 in Australian Open, 7638 in Roland Garros, 7915 in Wimbledon and 6087 in US Open). The study was approved by the local University Ethics Committee non-human subjects research and all procedures are conducted following the European General Data Protection Law in order to maintain the anonymity of sampled players.
Procedures
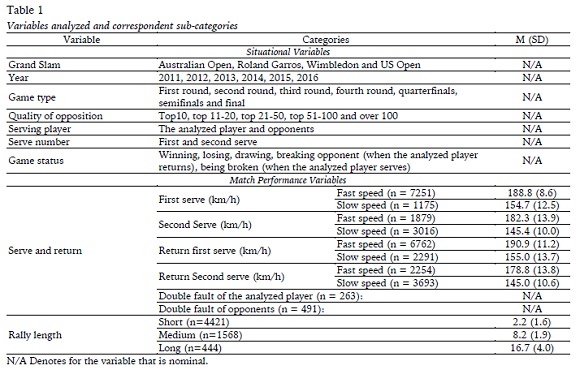
The Table 1 presents seven contextual variables and two performance-related variables that were included as predictor variables for point outcome (win/lose).
Based on the importance of Top-100 ranking that the previous research has continuously addressed (Prieto-Bermejo & Gómez-Ruano, 2016; Reid et al., 2010; Reid, Morgan, Churchill, & Bane, 2014), we have established five categories to classify the quality of opposition, using Top-10, Top-20, Top- 50 and Top-100 world ranking as cut value. In addition, as there are few studies that have addressed the issue of game status in tennis, we decided to define 5 situations of game status, considering the sequence of scores within every game, as is suggested by O’Donoghue and Brown (2009).
A two-step cluster analysis with Euclidean as the distance measure and Schwartz’s Bayesian criterion was used in the data package of IBM SPSS Statistics for Windows, Version 22.0 (Armonk, NY: IBM Corp.) to separately classify: (i). serve speed, and (ii) rally length (See Table 2). The serve speed was measured by km/h and the rally length was measured by count of the strokes (excluding serve) that two competing players interchange during a point. Former studies have discussed the tactical rationale of altering serve speed in the first or second serve (Gillet et al., 2009; Hizan et al., 2011; O’Donoghue & Brown, 2008), and the result of the cluster analysis automatically classified two serve speed categories, which was consistent with previous finding. Therefore, they were regarded as fast serve and slow serve speed.
Meanwhile, previous research showed that the rally length is classified into three categories: short (1 to 5 shots), regular (6 to 9 shots) and long (over 9 shots) (Lees, Kahn, & Maynard, 2004). The results of cluster analysis showed that three groups of rally length were automatically classified. The average number of each rally group had similarity with the abovementioned results, so that they were determined as short (2.2±1.6), medium (8.2±1.9) and long length (16.7±4.0) groups.
The reliability of the tracking data (serve speed) by Hawk-eye system were previously assessed, with an acceptable measuring error of around 3.6 mm (Mecheri, Rioult, Mantel, Kauffmann, & Benguigui, 2016; Reid et al., 2016; Whiteside & Reid, 2016). Additionally, two experienced performance analysts in tennis recollected the non-tracking notational (point sequence, point outcome, first and second serve and double faults) and rally data (rally length) of two matches that were randomly selected. The minimum Cohens kappa value for notational variables exceeded 0.90, demonstrating high inter-rater reliability (O’Donoghue, 2010).
Statistical analysis
Crosstabs command were performed with the use of Pearsons Chi-square test to analyze the effects between the point outcome and contextual variables related to Grand Slam, game type, set, quality of opposition, game status and point server. Effect sizes (ES) were calculated using the Cramers V test and their interpretation was based on the following criteria: 0.10 = small effect, 0.30 = medium effect, and 0.50 = large effect (Volker, 2006).
To have a refined understanding of the previous analysis, two classification trees with the exhaustive CHAID (Chi-square Interaction Detection) algorithm were used to model the relationship among point outcome and contextual variables. The first tree contained seven contextual variables and serve performance while the second considered seven contextual variables and rally performance. The algorithm is suitable for modelling nominal variables and has more precision because it merges categories until only two categories exist (Gómez, Battaglia, et al., 2015). The model was built under the following criteria: (i) the maximum number of iterations were 100; (ii) the minimum change in expected cell frequencies was 0.001; (iii) the significant values adjustment was done using the Bonferroni method; (iv) the tree based model has a maximum of 3 levels; (v) Grand Slam was forced
to be the first variable as court surfaces have direct impact on players tactical and technical performance (Gillet et al., 2009; O’Donoghue & Ingram, 2001). The risk of misclassification was calculated as a measure of the reliability of the model. The statistical analyses were done using the SPSS software (IBM SPSS Statistics for Windows, Version 22.0. Armonk, NY: IBM Corp.). The level of significance was set at p<0.05.
RESULTS
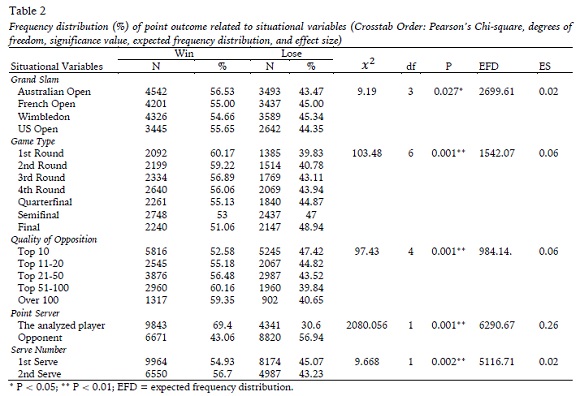
Table 2 shows the distribution of Grand Slam, game type, quality of opposition, point server and serve number, which are related to point outcome (numbers and percentage). The variables related to game characteristics were shown to be significant and the analyzed player won comparatively more points in Australian Open while the percentage of points won was decreasing gradually in every round as the game type changed from the first round (60.2%) to the final (51.1%). The quality of opposition was significantly related to point outcome (p = 0.001, ES= 0.06), greater success percentage was reached when playing against Top 51-100 players (60.2%), and lower success percentage occurred when competing with Top 10 players (52.6%). The results for variables related to serve exhibited that server and number of serve were also significantly related to point outcome (p = 0.001, ES= 0.26 and p = 0.002, ES= 0.02, respectively). Higher success was achieved when the player was serving (69.4%) comparing to the situation when he returned the serve (43.1%). Whereas relatively more points were won when he or his opponent served a second serve (56.8%).
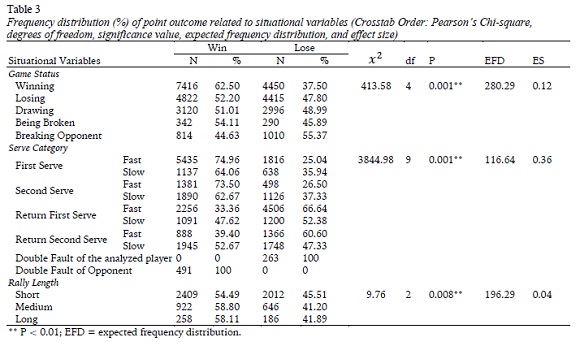
The sample distribution of game status, serve categories and rally length is presented in Table 3. The results demonstrated that game status had a significant relation with point outcome (p = 0.001, ES= 0.12), with higher point victory percentage when the player was wining (62.5%) than when he was trying to break the opponents service game (44.6%), and a relevantly greater success were shown when his service was being broken by the opponents (54.1%). Besides, the serve category was exhibited to be correlated significantly with the point outcome (p = 0.001, ES= 0.36). Serving fast in first and second serve enabled the player to win more points (75.0% and 73.5% respectively) while he had greater success of winning points when returned slow second serve (52.7%) than retuning other serves. Finally, rally length was also significantly associated to point outcome (p = 0.008, ES= 0.04). A medium to long rally helped him winning comparatively more points (58.8% and 58.1%, respectively) than short rally (54.5%).
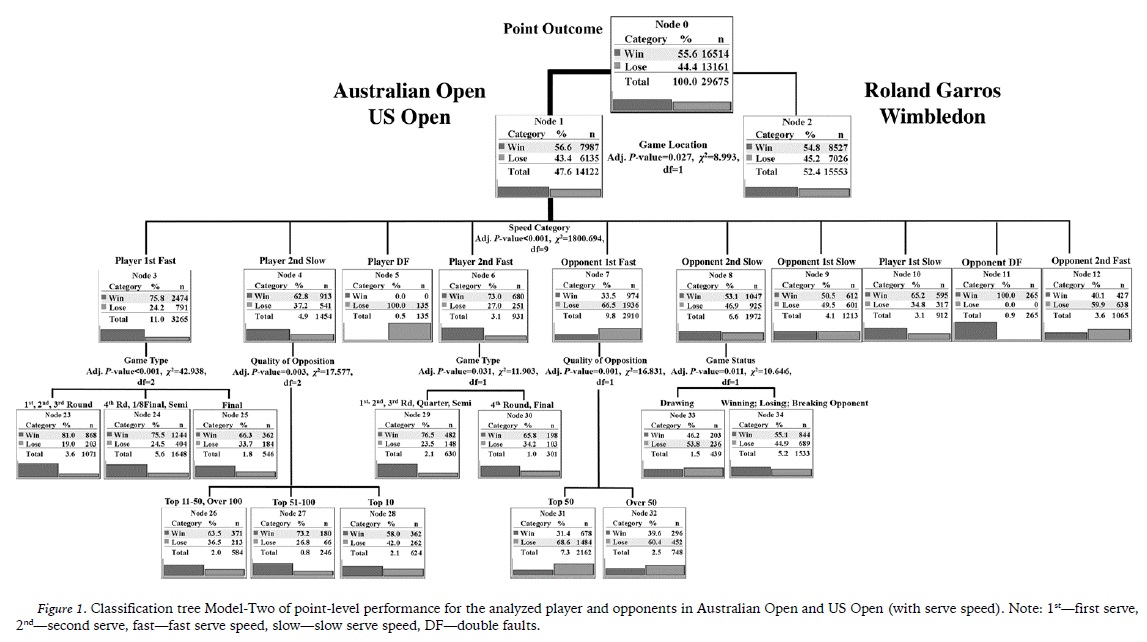
Figure 1 and 2 show the first exhaustive CHAID classification tree model for the player and his opponents. It was demonstrated that game location, serve category contributed strongly to the tree while game type, quality of opponent, game status also had an influence.
(clique para ampliar ! click to enlarge)
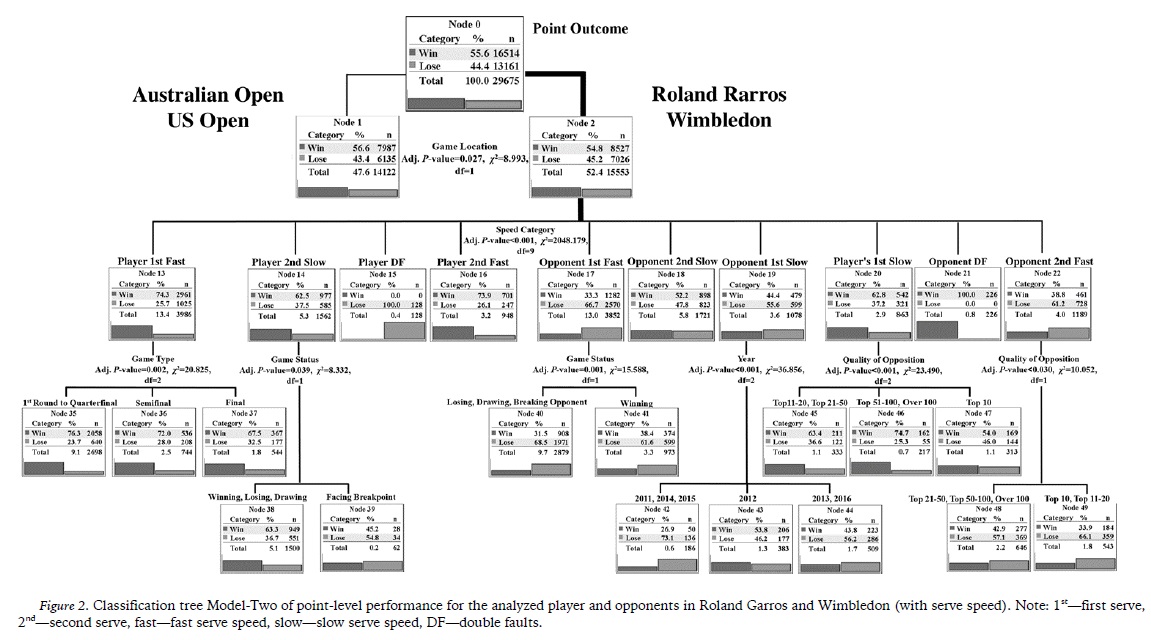
(clique para ampliar ! click to enlarge)
In Australian Open (AO) and US Open (US), the analyzed player won 56.6% of points, compared to 54.8% in Roland Garros (RG) and Wimbledon (W) (node 1 and 2). 75.8% and 73.0% of points were won when he served fast first and second serves in AO and US, while 74.3% and 73.9% were achieved for the ones in RG and W. In contrast, serving slow first and second serve made him win a lower 65.2% and 62.8% in AO and US, and 62.8% and 62.5% in RG and W. In terms of return, similar results of approximately 33% and 40% of points could be obtained in all slams while this player returned first and second fast serve. However, he could win 50.2% of points when returning slow second serve in AO and US (node 9), compared with 44.4% in RG and W (node 19). Lower winning percentage was obtained (node 25 and 37) when serving fast first serve in the final of all slams, compared to the previous rounds. In AO and US, serving slow second serves to Top 10 players achieved a lower 58% of points won (node 28), while in RG and W, this performance was influenced by game status in that this player won just 45.2% of points when facing breakpoints (node 39). Similarly, under the drawing game status in AO and US, he could win only 46.2% of points while returning slow second serves (node 33).
Figure 3 presents the second tree model that considered the rally performance. The results showed that point server and rally length were two variables that strongly contributed to the model. In all slams, the player won nearly 70% points in his service game (node 3 and 5) more than the 45% of return game (node 4 and 6). Finishing the points in short and long rally (node 12: 64.9% and node 11: 55.2%) during own service game helped him to win more points than medium rally, but it was not the case for Wimbledon, where only in medium rally could he win more points (node 13).

(clique para ampliar ! click to enlarge)
DISCUSSION
This study aimed to analyze the point-level performance of professional tennis players in different Grand Slams. Using the classification tree model, we try to explore a novel approach to assess the performance of player in relation to contextual variables.
Results showed that the performance of the analyzed player and his opponents was clearly influenced by game location, game type, quality of opposition, game status, point server, serve number, serve and return speed and rally length. In tennis, the effect of game location may consist in the following “venue variations”: temperature, humidity (Morante & Brotherhood, 2007), court surfaces (O’Donoghue & Ingram, 2001), surface abrasion, ball types and the distance between court and the audience (Dube & Tatz, 1991; McGarry et al., 2013). They are factors that players and coaches need to consider when planning match strategies. Grand Slam tournaments symbolize the maximum level of professional tennis (Cross & Pollard, 2009) and each slam is played on different court surface, which is speculated as the major influencing factor on players match-play (O’Donoghue & Ingram, 2001; Reid et al., 2016). Therefore, it is essential to have better understanding of its effect on players performance. In line with the study of Ma and his colleagues that male players were more likely to win a match in the US Open and Wimbledon than in the French Open (Ma, Liu, Tan, & Ma, 2013), our findings showed that the player of interest could win more points in Australian Open and US Open than in Roland Garros and Wimbledon. On the one hand, due to the slow court surface of Roland Garros, it was easier to break to the servers game and players tend to play more aggressively in return games. While in fast surface court of Wimbledon, serving players has greater advantage and it is hard to break their game, so that most players preferred to use safer playing style in fast court (Gillet et al., 2009; Tudor, Zecic, & Matkovic, 2014). On the other hand, it was also indicated that the analyzed player had a better familiarity with hard court surface.
Meanwhile, our findings indicated that the point performance of players was affected by game type. In Grand Slam tournaments, the influence of game type on players performance should be highlighted due to the fact that male player has to compete with a draw of 128 players within two weeks. Each match is played in the best of five sets. These factors affect the performance of player in a way that they have to adjust the strategy and tactics on a match-to- match basis to ensure the success as well as to avoid an early depletion of fitness and psychological state (Goossens, Kempeneers, Koning, & Spieksma, 2015; O’Donoghue, 2009). Goossens et al. (2015) showed that in Grand Slam, the previous match could have an effect on the next round for players and the possibility to win the next round will decrease if he played more games in previous match. In consistent with this finding, we also showed that as player proceeded into the next round, he could win less percentage of points. Besides, results of the classification tree demonstrated that the efficiency of serve performance was also conditioned by game type in all four slams, especially when the player served fast first and second serve. Serving fast in previous rounds could help him win more points while it was not the case in the last rounds, especially in the final. Obviously, this phenomenon should be examined together with the effect of quality of opposition (Cui, Gómez, Gonçalves, Liu, & Sampaio, 2017; Cui, Gómez, Gonçalves, & Sampaio, 2018) because in eliminatory tournament, the opponents of the next round are expected to be higher-ranked rivals with better competitive skills (Reid et al., 2010; Reid & Morris, 2013). Previous research that addressed the effect of opponents strength have identified that the serve and return performance of male players was influenced by quality of opposition (O’Donoghue, 2009; O’Donoghue & Cullinane, 2011). The present study provides more evidence on this issue. It was not surprising that higher winning percentage was achieved when the player competed with players ranked over Top 50 and then it descended when he was against Top 50, especially Top 10 players. However, the results from the classification tree offered more details on where and how the serve and return performance of this player was affected by different opponents. For instance, he turned out to win more points when playing with lower ranked players over Top 20 when serving slow first serve in Roland Garros and Wimbledon, whereas obtaining more points when returning fast first serves by over Top 50 opponents during Australian Open and US Open.
In elite tennis matches, winning the previous point particularly have a positive effect on winning the current point, and at crucial points the server has a disadvantage of winning because of the phychological pressure in streeful situations (Filipčič, Filipčič, & Berendija, 2008; Klaassen & Magnus, 2001), which suggested a score-line effect (Gómez, Lago, et al., 2013; O’Donoghue, 2012) within tennis game. In accordance with those previous findings, we used within-game status to assess the performance of tennis player. Results revealed that the player had highest winning chance when he was winning, while he was losing, the percentage decreased significantly. Furthermore, the first classification tree (Figure 1) showed that the players slow second serve was influenced by game status in Roland and Wimbledon, where he won more points when he was winning, losing or drawing but less than half of all points when facing breakpoint. When he returned second slow serve in AO and UO, he had more success when winning, losing or breaking opponents than when he was drawing. This suggested that the positive effect of winning the previous point on winning the current one. However, future research should consider players performance in critical points, such as set points, tie-break points and match points.
Furthermore, the results revealed the influence of rally length on performance. And in agreement with the previous research in that server has an advantage in points lasted to 4 shots (O’Donoghue & Brown, 2008), our findings that short rally and long rally in this players service game helped him to win more points than medium rally. In return game, he could win more points in medium to long rallies.
Admittedly, the generalizability of our findings could be limited because of the sample size and failure to consider players injury status. However, it is important to note that the sampled data are longitudinal and representative of elite tennis players, as all sampled players were included in the main-draws of Grand Slams.
CONCLUSION
The results of the current study demonstrate the usefulness of the exhaustive CHAID tree model to interpret the match performance of tennis player and it allows to develop individual performance profiles. Although the court surfaces had a major effect on players performance, our findings suggested that this importance should be considered together with others performance indicators such as game type, quality of opposition, match status. From a practical perspective, efforts could be made to improve the players return performance, especially the second serve return when he was in critical game status like drawing, having breaking opportunity or being broken, and furthermore, to attempt playing aggressively to win return points in short rally. These results will give insightful ideas for coaches and players when planning the game strategy, helping to modify training contents to resemble real match situations where player learn to be more adaptable to play in different game status. Furthermore, it is possible that performance analysts in tennis use this method to model multi-player performance for specific match situations or in a time-wise manner.
REFERENCES
Butterworth, A., O’Donoghue, P., & Cropley, B. (2013). Performance profiling in sports coaching: a review. International Journal of Performance Analysis in Sport, 13(3), 572-593.
Cross, R., & Pollard, G. (2009). Grand Slam mens singles tennis 1991-2009 Serve speeds and other related data. Coaching & Sport Science Review, 16(49), 8-10. [ Links ]
Cui, Y., Gómez, M. A., Gonçalves, B., Liu, H., & Sampaio, J. (2017). Effects of experience and relative quality in tennis match performance during four Grand Slams. International Journal of Performance Analysis in Sport, 17(5), 1-19. DOI: 10.1080/24748668.2017.1399325. [ Links ]
Cui, Y., Gómez, M. Á., Gonçalves, B., & Sampaio, J. (2018). Performance profiles of professional female tennis players in grand slams. Plos One, 13(7), e0200591. DOI: 10.1371/journal.pone.0200591. [ Links ]
Dube, S. K., & Tatz, S. J. (1991). Audience effects in tennis performance. Perceptual and motor skills, 73(3), 844-846. [ Links ]
Filipčič, T., Filipčič, A., & Berendija, T. (2008). Comparison of game characteristics of male and female tennis players at Roland Garros 2005. Acta Universitatis Palackianae Olomucensis. Gymnica, 38(3), 21-28.
Galé-Ansodi, C., Castellano, J., & Usabiaga, O. (2016). Effects of different surfaces in time-motion characteristics in youth elite tennis players. International Journal of Performance Analysis in Sport, 16(3), 860-870. [ Links ]
Gillet, E., Leroy, D., Thouvarecq, R., & Stein, J. F. (2009). A Notational Analysis of Elite Tennis Serve and Serve-Return Strategies on Slow Surface. Journal of Strength and Conditioning Research, 23(2), 532-539. DOI: 10.1519/JSC.0b013e31818efe29. [ Links ]
Gómez, M. Á., Battaglia, O., Lorenzo, A., Lorenzo, J.,Jiménez, S., & Sampaio, J. (2015). Effectiveness during ball screens in elite basketball games. Journal of Sports Sciences, 33(17), 1844-1852. [ Links ]
Gómez, M. Á., Lago, C., & Pollard, R. (2013). Situational variables. In T. McGarry, P. O’Donoghue, & J. Sampaio (Eds.), Routledge handbook of sports performance analysis (pp. 259- 269). London: Routledge.
Gómez, M. Á., Lorenzo, A., Ibañez, S.-J., & Sampaio, J. (2013). Ball possession effectiveness in men’s and women’s elite basketball according to situational variables in different game periods. Journal of Sports Sciences, 31(14), 1578-1587. DOI: 10.1080/02640414.2013.792942.
Gómez, M. Á., Moral, J., & Lago-Peñas, C. (2015). Multivariate analysis of ball possessions effectiveness in elite futsal. Journal of Sports Sciences, 33(20), 2173-2181. DOI: 10.1080/02640414.2015.1075168. [ Links ]
Goossens, D. R., Kempeneers, J., Koning, R. H., & Spieksma, F. C. R. (2015). Winning in straight sets helps in Grand Slam tennis. International Journal of Performance Analysis in Sport, 15(3), 1007-1021. [ Links ]
Hizan, H., Whipp, P., & Reid, M. (2011). Comparison of serve and serve return statistics of high performance male and female tennis players from different age-groups. International Journal of Performance Analysis in Sport, 11(2), 365-375. DOI: 10.1080/24748668.2011.11868556. [ Links ]
Hughes, M., & Franks, I. (2015). Essentials of performance analysis in sport. London: Routledge. [ Links ]
Klaassen, F. J., & Magnus, J. R. (2001). Are points in tennis independent and identically distributed? Evidence from a dynamic binary panel data model. Journal of the American Statistical Association, 96(454), 500-509. [ Links ]
Lago-Peñas, C. (2012). The Role of Situational Variables in Analysing Physical Performance in Soccer. Journal of Human Kinetics, 35, 89-95. DOI: 10.2478/v10078-012-0082-9. [ Links ]
Lago-Peñas, C., Gómez-Ruano, M., Megías-Navarro, D., & Pollard, R. (2016). Home advantage in football: Examining the effect of scoring first on match outcome in the five major European leagues. International Journal of Performance Analysis in Sport, 16(2), 411-421. [ Links ]
Lees, A., Kahn, J.-F., & Maynard, I. W. (2004). Science and Racket Sports III: The Proceedings of the Eighth International Table Tennis Federation Sports Science Congress and the Third World Congress of Science and Racket Sports: Psychology Press. [ Links ]
Ma, S. M., Liu, C. C., Tan, Y., & Ma, S. C. (2013). Winning matches in Grand Slam men’s singles: An analysis of player performance-related variables from 1991 to 2008. Journal of Sports Sciences, 31(11), 1147-1155. DOI: 10.1080/02640414.2013.775472.
McGarry, T., O’Donoghue, P., & Sampaio, J. (2013). Routledge handbook of sports performance analysis: Routledge.
Mecheri, S., Rioult, F., Mantel, B., Kauffmann, F., & Benguigui, N. (2016). The serve impact in tennis: First large-scale study of big Hawk-Eye data. Statistical Analysis and Data Mining: The ASA DataScience Journal, 9(5), 310-325. DOI: 10.1002/sam.11316. [ Links ]
Morante, S. M., & Brotherhood, J. R. (2007). Air temperature and physiological and subjective responses during competitive singles tennis. British Journal of Sports Medicine, 41(11), 773-778. [ Links ]
O’Donoghue, P. (2009). Interacting Performances Theory. International Journal of Performance Analysisin Sport, 9(1), 26-46. [ Links ]
O’Donoghue, P. (2010). Research methods for sports performance analysis. London: Routledge. [ Links ]
O’Donoghue, P. (2012). Break points in Grand Slam men’s singles tennis. International Journal of Performance Analysis in Sport, 12(1), 156-165.
O’Donoghue, P., & Brown, E. (2009). Sequences of service points and the misperception of momentum in elite tennis. International Journal of Performance Analysis in Sport, 9(1), 113-127. [ Links ]
O’Donoghue, P., & Cullinane, A. (2011). A regression- based approach to interpreting sports performance. International Journal of Performance Analysis in Sport, 11(2), 295-307. [ Links ]
O’Donoghue, P., & Ingram, B. (2001). A notational analysis of elite tennis strategy. Journal of Sports Sciences, 19(2), 107-115. DOI: 10.1080/026404101300036299. [ Links ]
O’Donoghue, P. G., & Brown, E. (2008). The importance of service in Grand Slam singles tennis. International Journal of Performance Analysis in Sport, 8(3), 70-78. [ Links ]
Ofoghi, B., Zeleznikow, J., MacMahon, C., & Raab, M. (2013). Data mining in elite sports: a review and a framework. Measurement in Physical Education and Exercise Science, 17(3), 171-186. [ Links ]
Prieto-Bermejo, J., & Gómez-Ruano, M. Á. (2016). Entering tennis mens Grand Slams within the top-10 and its relationship with the fact of winning the tournament.[Acceder a los Grand Slams de tenis masculino desde el top-10 y su relación con el hecho de ganar el torneo]. RICYDE. Revista Internacional de Ciencias del Deporte. DOI: 10.5232/ricyde,12(46),410-422.
Reid, M., McMurtrie, D., & Crespo, M. (2010). Title: The relationship between match statistics and top 100 ranking in professional men’s tennis. International Journal of Performance Analysis in Sport, 10(2), 131-138.
Reid, M., Morgan, S., Churchill, T., & Bane, M. K. (2014). Rankings in professional mens tennis: a rich but underutilized source of information. Journal of Sports Sciences, 32(10), 986-992. DOI: 10.1080/02640414.2013.876086. [ Links ]
Reid, M., Morgan, S., & Whiteside, D. (2016). Matchplay characteristics of Grand Slam tennis: implications for training and conditioning. Journal of Sports Sciences, 34(19), 1791-1798. DOI: 10.1080/02640414.2016.1139161. [ Links ]
Reid, M., & Morris, C. (2013). Ranking benchmarks of top 100 players in men’s professional tennis. European Journal of Sport Science, 13(4), 350-355. DOI: 10.1080/17461391.2011.608812.
Robertson, S., Back, N., & Bartlett, J. D. (2016). Explaining match outcome in elite Australian Rules football using team performance indicators. Journal of Sports Sciences, 34(7), 637-644. [ Links ]
Sanchez-Pay, A., Palao, J. M., Torres-Luque, G., & Sanz-Rivas, D. (2015). Differences in set statistics between wheelchair and conventional tennis on different types of surfaces and by gender. International Journal of Performance Analysis in Sport, 15(3), 1177-1188. [ Links ]
Tudor, P. B., Zecic, M., & Matkovic, B. (2014). Differences between 2010 and 2011 performance indicators of tennis play at the grand slam tournaments. Kinesiology, 46, 101-106. [ Links ]
Volker, M. A. (2006). Reporting effect size estimates in school psychology research. Psychology in the Schools, 43(6), 653-672. DOI: 10.1002/pits.20176. [ Links ]
Whiteside, D., & Reid, M. (2016). Spatial characteristics of professional tennis serves with implications for serving aces: A machine learning approach. Journal of Sports Sciences, 35(7), 1-7. DOI: 10.1080/02640414.2016.1183805. [ Links ]
Acknowledgments: Nothing to declare.
Funding: The study was supported by National Key R&D Program of China (2018YFC2000600). The first author was supported by the China Postdoctoral Science Foundation and the Fundamental Research Funds for the Central Universities (2019QD033). This study is part of Beijing Sport University Double First Class University Plan [2018GJ002].
Conflict of interests: Nothing to declare.
Manuscript received at January 6th 2019; Accepted at February 2nd 2019
[*]Corresponding author: Informational Road No. 48, Haidian District, 100084 Beijing, China
Email: liuhaoyang@bsu.edu.cn