Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Lusófona de Educação
versão impressa ISSN 1645-7250
Rev. Lusófona de Educação no.25 Lisboa dez. 2013
Pré-cálculo e a formação inicial de professores de Matemática: resultados preocupantes de um teste diagnóstico
Precalculus and the education of pre-service teachers of Mathematics Worrying results of a diagnostic test
Pré-calcul et l’ éducation initiale des enseignants de Mathématiques Résultats inquiétants d’un test diagnostic
El pre-cálculo y la formación inicial del profesorado de Matemáticas Los resultados preocupantes de una prueba diagnóstica
Susana Fernandes*, Ana C. Conceição **
*Doutora em Matemática. Professora Auxiliar do Departamento de Matemática, da Faculdade de Ciências e Tecnologia, da Universidade do Algarve. Membro fundador do Centro de Estudos e Desenvolvimento da Matemática no Ensino Superior (CEDMES), da Universidade do Algarve. Membro do Centro de Investigação Operacional (CIO), da Faculdade de Ciências da niversidade de Lisboa.
e-mail: sfer@ualg.pt
**Doutora em Matemática. Professora Auxiliar do Departamento de Matemática, da Faculdade de Ciências e Tecnologia, da Universidade do Algarve. Membro fundador do Centro de Estudos e Desenvolvimento da Matemática no Ensino Superior (CEDMES), da Universidade do Algarve. Membro do Centro de Análise Funcional e Aplicações (CEAF), do Instituto Superior Técnico.
e-mail: aconcei@ualg.pt
RESUMO
A adaptação ao processo de Bolonha, ao reduzir as licenciaturas para três anos de escolaridade, impulsionou a criação de mestrados que têm por objectivo formar professores profissionalizados. Encontramos na literatura inúmeros trabalhos que referem ser necessário, na formação de futuros professores, apostar no domínio dos conteúdos que vão ser lecionados nos níveis de ensino para os quais conferem a habilitação para a docência, sem esquecer a importante aquisição de todo o tipo de competências inerentes ao ensino. Neste artigo apresentamos dados relativos a licenciados em Matemática que frequentam um Mestrado em Ensino. Com o intuito de aferir os seus conhecimentos, na área de pré-cálculo, foi elaborado um teste diagnóstico, respondido presencialmente antes e depois desses conteúdos serem abordados em sala de aula, tendo sido identificadas diversas lacunas de conhecimento. Discutimos os diferentes tipos de erros cometidos, exemplificando as fragilidades científicas existentes. Concluímos a necessidade de criação de disciplinas pensadas especificamente para o conhecimento do conteúdo a lecionar; um fator determinante para um futuro de sucesso de qualquer professor de Matemática.
Palavras-chave: formação inicial de professores; professores de Matemática; cursos pós-Bolonha; pré-cálculo, Wolfram|Alpha
ABSTRACT
Adapting graduate degrees to the Bologna process reduced its duration to three scholar years. This promoted the creation of Masters in Teaching, the required degree to become an accredited teacher. Existing literature on training future teachers indicates the need for focusing on the mathematical (content) knowledge for teaching the subject matters of the curricula that will be taught, while not disregarding the acquisition of all teaching abilities.
In this article we present data which reveals the lack of a strong scientific knowledge regarding the mathematical field of precalculus, of pre-service teachers attending a master degree in teaching Mathematics in junior high and high school levels. A diagnostic test was designed to measure the content knowledge in precalculus of these master students. They answered the same diagnostic test questions before and after the contents were addressed in the classroom.
This paper presents different kinds of problems in their answers, exposing the mathematical weaknesses of these pre-service teachers in this field. These weaknesses are evident in solving equations and inequations and also in solving limits. We choose to present the two questions of the diagnostic test that illustrate these facts. There are three kinds of errors in the answers to the question of solving equations: the misuse of the Ruffini’s rule; the inability to find the correct domain of the expressions and the misuse of disjunctions/conjunctions symbols. Only 29% of the pre-service teachers solved correctly this test question before attending the precalculus classes. After attending classes the percentage of correct answers was 50%. There are three kinds of errors in the answers to the question of solving limits: basic errors, like misusing the distributive property of the multiplication operation over the addition operation or failing to solve simple derivatives; not knowing the module function and the inability to deal with indeterminations. Before attending the precalculus classes none of the pre-service teachers gave a correct answer to this diagnostic test question. The same happened one year after they attended the classes. All the answers to both questions revealed a strong lack of vocabulary knowledge and an unacceptable inability to use terms and notation correctly. This document concludes by stressing the need for the existence of graduate courses which specifically address mathematical knowledge for teaching; a crucial factor for a successful practice of pre-service teachers.
Key-words: Education of pre-service teachers, Teachers of Mathematics, Post- Bologna degrees, Precalculus, Wolfram|Alpha
RÉSUMÉ
L’adaptation des grades universitaires du premier cycle au processus de Bologne a réduit sa durée à trois années. Cette décision a obligé la création des Maîtrises en enseignement, le degré requis pour devenir un enseignant titulaire. La littérature sur la formation initiale des enseignants indique que cette formation doit se concentrer sur les connaissances spécifiques des programmes d’études qui seront enseignés. En même temps on doit assurer l’acquisition de toutes les compétences d’enseignement. Notre étude révèle que les étudiants qui fréquentent une maîtrise en enseignement de mathématiques ont une connaissance insuffisante dans le domaine mathématique du pré-calcul. On a conçu un test diagnostic pour mesurer la connaissance du contenu en pré-calcul de ces futurs enseignants.
Ils ont répondu aux mêmes questions du test diagnostic après les leçons sur le sujet. Cet article présente les différents types d’erreurs dans leurs réponses, exposant les faiblesses mathématiques des futurs enseignants dans ce domaine.
Nous concluons en soulignant la nécessité de l’existence de disciplines dévouées spécifiquement aux matières des programmes d´études de l’école élémentaire ou secondaire, étant donné qu’il s’agit d’un facteur crucial pour la réussite professionnelle des futurs enseignants.
Mots-clés: formation initiale des enseignants; professeurs de Mathématiques; cours post-Bologne; pré-calcul; Wolfram|Alpha
RESUMEN
La reducción de la duración de las licenciaturas para tres años que resultó de la adopción del proceso de Boloña, ocasionó la creación de maestrías que tienen como objetivo formar profesores especializados. En la literatura encontramos numerosos trabajos que refieren la necesidad de formar futuros profesores que dominen contenidos científicos específicos para habilitar a los alumnos a ejercer una actividad docente particular, sin olvidar la importancia de adquirir competencias genéricas inherentes a la docencia.
En este artículo presentamos datos relativos a licenciados en Matemática que frecuentan una maestría en Educación. Con el propósito de evaluar los conocimientos de los alumnos de esta maestría, fue realizado un examen diagnóstico en la materia de pre-cálculo. Este examen, que fue respondido de forma presencial por los alumnos antes y después de haber dado los contenidos de la materia en el salón de clase, permitió identificar varias lagunas de conocimiento. Discutimos los diferentes tipos de errores cometidos, ilustrando las fragilidades científicas existentes. Concluimos que la creación de materias pensadas específicamente para el área de conocimiento que va a ser enseñada es un factor determinante para asegurar el éxito futuro de cualquier profesor de Matemática.
Palabras clave: formación inicial del profesorado; profesores de Matemáticas; cursos post-Boloña; pre-cálculo; Wolfram | Alpha
Introdução
O conhecimento do conteúdo é, sem qualquer dúvida, um fator determinante para um futuro de sucesso de qualquer professor. É inquestionável que o conhecimento dos conteúdos presentes nas disciplinas de álgebra linear, de cálculo diferencial em Rn, de cálculo integral em Rn, de equações diferenciais, de análise complexa, de análise funcional, são imprescindíveis para o desenvolvimento intelectual e para o amadurecimento matemático de qualquer futuro professor de Matemática. No entanto, o conhecimento (mesmo que intensamente explorado) desses conteúdos é necessário mas não suficiente para uma boa formação dos futuros professores para o exercício da atividade docente e, em particular, para o ensino de conteúdos do ensino secundário, tais como álgebra, trigonometria, pré-cálculo, etc.. Além disso, atualmente existem conteúdos do ensino secundário que não são abordados nas Licenciaturas em Matemática, nomeadamente o tema de Métodos de Apoio à Decisão. A diminuição para três anos de escolaridade das licenciaturas devido a adaptação a Bolonha, além de afetar significativamente o conhecimento de conteúdos adquiridos pelos atuais professores em formação inicial, é responsável pela criação de mestrados, em diversas áreas de especialização, que têm por objectivo formar professores profissionalizados em diversos níveis de ensino, conferindo simultaneamente o grau de mestre e a habilitação para a docência. A literatura refere que a formação de futuros professores preparando os alunos para a futura atividade docente e conferindo estatuto profissional, deve apostar na aquisição de competências (pedagógicas e outras) para ensinar, sem esquecer a importância do domínio dos conhecimentos científicos que vão ser ensinados nos níveis de ensino para os quais se confere a habilitação para a docência. De fato, “Nos dias de hoje, formar professores coloca desafios cada vez mais exigentes a quem o idealiza, organiza e implementa.” (Rocha, 2006).
Neste artigo iremos expor as nossas preocupações relativamente à formação científica dos licenciados pós-Bolonha em Matemática, em Portugal. Como base utilizaremos a nossa experiência no ensino de uma unidade curricular, de um Mestrado em Ensino de Matemática, criada como disciplina de opção na área científica de docência.
A nossa experiência leva-nos a concluir que os alunos que frequentaram a disciplina (a funcionar pela primeira vez) apresentavam grandes lacunas de conhecimento científico em diversas áreas da Matemática, em particular na área do pré-cálculo, assunto que abordamos neste documento. Com o intuito de aferir os conhecimentos científicos dos alunos nesta área foi elaborado um teste diagnóstico a que os alunos responderam presencialmente antes e depois desses conteúdos programáticos serem discutidos e aprofundados cientificamente em sala de aula. Neste artigo apresentamos algumas respostas dadas por alunos que exemplificam as diversas fragilidades científicas existentes, supomos nós, na generalidade dos recém licenciados em Matemática.
Este documento está estruturado da seguinte forma: Segue-se uma secção dedicada à revisão da literatura relevante para este trabalho. Prossegue com a descrição da disciplina e depois com a descrição dos alunos que a frequentaram.
De seguida descrevemos duas das questões do teste diagnóstico elaborado e apresentamos algumas das respostas dos alunos, considerando diferentes tipos de lacunas reveladas. O documento termina com algumas reflexões e sugestões.
Revisão da Literatura
O sociólogo Perrenoud (1999) enumera “dez novas competências para ensinar”, sendo a primeira delas o saber organizar e dirigir situações de aprendizagem, e para tal é imprescindível que o professor domine os conteúdos a lecionar. O estudo realizado por Conceição e Sousa (2012) revela que esta competência é também das mais valorizadas pelos professores no exercício da sua profissão.
Nos anos 80, pela mão de Shulman, a investigação no ensino da Matemática volta a debruçar-se sobre a questão do conhecimento do conteúdo. Até então estava centrada em aspectos como conhecimentos gerais de pedagogia (gestão em sala de aula, etc.), conhecimento dos alunos e suas características, conhecimento dos contextos de ensino (contexto da turma, gestão escolar, caracterização das comunidades e das culturas, etc.) e conhecimento dos propósitos, valores, filosofias e fundamentos históricos do ensino. Shulman, em (1987) refere a falta de investigação sobre o conhecimento do conteúdo (conhecimento dos assuntos e da sua subjacente estrutura de organização), o conhecimento do curriculum (conhecimento dos programas desenhados para ensinar os assuntos a determinado nível, conhecimento dos materiais existentes adequados para esse ensino e o conhecimento de indicações ou contra-indicações para o uso desses materiais de acordo com as circunstâncias) e o que Shulman havia designado já em (1986) como conhecimento pedagógico do conteúdo, e que definiu como sendo o conhecimento das formas mais úteis de representar e formular os assuntos para os tornar compreensíveis para outros (ilustrações, exemplos, analogias, exposições, demonstrações) incluindo também o entendimento do que torna a aprendizagem de determinado tópico fácil ou difícil (conceitos e preconceitos de alunos de diferentes idades ou diferentes formações).
Ball, Thames & Phelps (2008) definem o domínio do conhecimento matemático para ensinar. Obviamente os professores têm de saber o conteúdo que ensinam, mas para o ensinar precisam de saber mais. Interessa identificar o que mais precisam de saber e de que forma precisam de o saber para o seu uso efectivo ao ensinarem. É inquestionável que o trabalho de professor necessita de um tipo especial de conhecimento matemático. Isto sugere que a forma de formar futuros professores, por exemplo na área de pré-cálculo, tem de ter em conta quando e onde esse conhecimento será necessário no seu trabalho de professores. Implicando ainda que sejam explícitas as conexões entre o conhecimento dos conteúdos e a forma de os ensinar. Estes autores consideram que definindo o domínio do conhecimento matemático para ensinar desta forma será possível não só estabelecer prioridades sobre os conteúdos a incluir na formação de futuros professores mas também aumentar as perspectivas de que estes sejam capazes de usar o que aprenderam na sua prática de ensino. Ball, Thames & Phelps (2008) subdividem a categoria de conhecimento do conteúdo definida por Shulman em duas: conhecimento comum do conteúdo e conhecimento especializado do conteúdo. Este conhecimento especializado não será necessariamente o conhecimento dos “matemáticos” mas antes um conhecimento estreitamente ligado à prática de ensino, por exemplo, um raciocínio matemático que permita uma análise eficiente e em tempo útil de erros cometidos por alunos, ou determinar se uma forma de resolução alternativa funciona em geral ou não, e porquê. Os autores subdividem também a categoria de conhecimento pedagógico do conteúdo de Shulman em três: conhecimento do conteúdo e dos alunos (saber o tipo de erros mais frequentes, saber se um tópico é mais ou menos difícil para os alunos, etc.), conhecimento do conteúdo e da técnica de ensinar (saber que exemplo escolher para introduzir ou para aprofundar um tópico, saber quando utilizar uma questão de um aluno para evidenciar uma determinada propriedade, etc.) e conhecimento do curriculum (conhecimento dos programas desenhados para ensinar os assuntos a determinado nível, conhecimento dos materiais existentes adequados para esse ensino e o conhecimento de indicações ou contra-indicações para o uso desses materiais de acordo com as circunstâncias).
Como é referido em Hodge, Gerberry, Moss & Staples (2010) os futuros professores partilham, na maioria das vezes, as disciplinas dos seus planos de estudos com alunos que pretendem seguir carreira em Matemática, Ciências Naturais, engenharias ou tecnologias. Ora enquanto que os outros profissionais necessitam de aplicar a Matemática a problemas práticos ou, no caso dos matemáticos, investigar avanços científicos na área, os futuros professores precisam de tornar a Matemática (mais ou menos básica) acessível aos seus alunos. Com base nestas diferenças inúmeras vozes se têm pronunciado pela necessidade de disciplinas específicas para futuros professores de Matemática. Hodge, Gerberry, Moss & Staples (2010) examinam o papel que disciplinas de Matemática dos cursos de 1.º ciclo desempenham na formação de futuros professores de Matemática. Neste sentido os autores questionaram professores universitários de Matemática sobre o que pensam que os futuros professores necessitam para ser bons professores; e também sobre as suas percepções relativamente ao contributo dado pelas suas disciplinas para formar bons professores de Matemática. Os professores universitários de Matemática valorizaram a aquisição por parte dos futuros professores de uma visão abrangente da Matemática, percebendo como esta é um sistema construído a partir de um conjunto de axiomas base, percebendo as interligações entre diferentes tópicos e incorporando uma visão da Matemática como um processo que envolve resolução de problemas, criatividade, experimentação e não uma visão redutora de um corpo de conhecimento imutável a memorizar e reproduzir. Enquanto que a caracterização de um bom professor de Matemática do ensino secundário pareceu bem definida para todos os intervenientes no estudo, a identificação do contributo directo das disciplinas que lecionam para a aquisição de competências necessárias aos futuros professores foi mais difusa.
No trabalho Wilburne & Long (2010), desenvolvido nos Estados Unidos, foi pedido a 70 futuros professores de Matemática do ensino secundário que resolvessem os exames estatais para avaliação de alunos do 11º ano. Os exames incluem questões das seguintes 5 áreas: números e operações, geometria, álgebra e funções, análise de dados e probabilidades e pré-cálculo. Em cada questão foi acrescentada a hipótese de responder “não sei resolver esta questão”. A proporção média de respostas correctas para estas 5 áreas, por esta ordem foi: 0.86, 0.84, 0.79, 0.78 e 0.37. A proporção média de respostas “não sei resolver esta questão” foi para as 5 áreas, pela ordem descrita: 0.01, 0.03, 0.05, 0.06 e 0.36. É gritante a falta de preparação na área de pré-cálculo dos futuros professores de Matemática que participaram neste estudo. Este trabalho revelou também, e como seria de esperar, a existência de correlação entre o conhecimento do conteúdo e o conhecimento de vocabulário. Assim como entre o conhecimento do conteúdo e o conforto/confiança dos futuros professores no ensino do conteúdo.
Todos estes trabalhos, e os trabalhos que referenciam, reforçam a necessidade da existência de programas de educação em Matemática que apoiem conexões entre os conteúdos dos cursos de nível universitário, os conteúdos do ensino secundário e os métodos de ensino dos diversos conteúdos, isto é, o conhecimento pedagógico dos conteúdos.
Descrição da disciplina
A experiência de ensino relatada neste trabalho refere-se a uma disciplina lecionada num Mestrado em Ensino em Matemática no 3º Ciclo do Ensino Básico e no Ensino Secundário que tem por objetivo formar professores profissionalizados, conferindo simultaneamente o grau de mestre e a habilitação para a docência. O mestrado, que pretende formar candidatos a professores fornecendo formação atualizada e avançada, só possui uma disciplina (semestral) na área de formação. Conhecendo os planos de estudo das atuais Licenciaturas (pós-Bolonha) em Matemática, uma única disciplina na área da Matemática é sem dúvida insuficiente para formar professores, possuidores de sólido conhecimento científico e com competências necessárias ao exercício da profissão. Sendo a referida disciplina opcional, ao criá-la optámos por propor uma Unidade Curricular com o intuito de desenvolver competências que são específicas da atividade profissional dos futuros professores, nomeadamente a capacidade de cálculo, o conhecimento de resultados matemáticos, a capacidade de generalização e abstração, a capacidade de formular e resolver problemas e a argumentação lógica e espírito crítico. Pretendeu-se ainda dotar os alunos com um conjunto de conhecimentos teóricos e práticos ao nível da Matemática e incutir-lhes a necessidade de rigor no uso da linguagem, e a clareza na exposição. De acordo com a opinião expressa em Wilboourne & Long (2010) sobre o que se passa nos Estados Unidos da América, também em Portugal ocorre o desfasamento entre os conteúdos lecionados no ensino superior e os conteúdos dos programas do 3º ciclo do ensino básico e do ensino secundário, uma vez que não existem Licenciaturas em Matemática específicas para futuros mestres em Ensino em Matemática. Na idealização da disciplina optámos pois por revisitar, discutir e aprofundar cientificamente alguns destes conteúdos programáticos, nomeadamente nas áreas do pré-cálculo, do cálculo diferencial, da estatística e das probabilidades e dos métodos de apoio à decisão. Os conteúdos programáticos abordados, relativos ao pré-cálculo e cálculo diferencial (números e operações, equações, inequações, limites, derivadas, funções e gráficos), foram explorados com o Wolfram|Alpha (http://www.wolframalpha.com/) e o Wolfram Demonstrations Project (http://demonstrations.wolfram.com). Com o intuito de exemplificar determinados conteúdos foi também utilizado o sistema de álgebra computacional Mathematica. A utilização destas ferramentas permite aos alunos uma melhor compreensão dos conteúdos que irão lecionar pois aprendem como é possível realizar (com recurso ao computador) um número considerável de tarefas/exercícios. Nessa disciplina os alunos foram avaliados relativamente aos seus conhecimentos do conteúdo e ao conhecimento do vocabulário.
Tentámos também analisar a sua confiança no futuro ensino de diversos temas. Pretendeu-se que o aluno que obtivesse aprovação nesta disciplina fosse capaz de encarar com segurança, competência e sucesso o ensino de todos os temas abordados, assim como a elaboração de vários tipos de provas adequadas aos vários conteúdos programáticos abordados.
Descrição dos alunos
Os nove alunos que frequentaram a disciplina fizeram as suas licenciaturas pós-Bolonha em diversas universidades públicas do país, com média final de curso a variar entre os doze e os catorze valores. Sendo a disciplina uma de várias opções oferecidas na área de formação de docência os alunos justificaram a sua escolha tendo em conta os conteúdos programáticos abordados, nomeadamente o tópico de métodos de apoio à decisão, não lecionado nas suas licenciaturas, e também as reconhecidas falhas no conhecimento do conteúdo e vocabulário do tópico de pré-cálculo. Cerca de metade destes futuros professores tem experiência como explicador de Matemática a estudantes do 3º ciclo do ensino básico, do ensino secundário e até do ensino superior.
Teste diagnóstico
Com o intuito de aferir os conhecimentos científicos dos alunos na área de pré-cálculo foi elaborado um teste diagnóstico a que os alunos responderam de forma anónima e presencialmente antes desses conteúdos programáticos serem discutidos e aprofundados cientificamente. As questões selecionadas para este teste foram escolhidas tendo em conta a experiência de lecionação de Matemática a outros cursos, focando-se nos pontos onde habitualmente são detetadas mais dificuldades. No geral as resoluções dos alunos foram bem sucedidas ten-do as maiores dificuldades sido observadas na resolução de equações e inequações e no cálculo de limites. Neste artigo apresentamos algumas respostas dadas pelos alunos a duas das questões do teste, que exemplificam as diversas fragilidades científicas existentes. Escolhemos expor as duas questões onde, como previsto, foram observadas mais dificuldades e apresentamos respostas dos alunos que exemplificam todos os diferentes tipos de erros observados.
Com o objectivo de averiguar se foram alcançados os resultados esperados de aprendizagem nomeadamente no conhecimento e no rigor do uso de linguagem e clareza de exposição; as mesmas duas questões selecionadas foram apresentadas para resolução no ano letivo seguinte, estando os referidos alunos em prática de ensino supervisionada. O tempo decorrido entre as duas solicitações aos alunos para que resolvessem o teste diagnóstico é de um ano. Optámos por não pedir aos alunos que resolvessem uma segunda vez o teste diagnóstico imediatamente após o funcionamento da disciplina para poder testar a solidez do processo de aquisição de novos conhecimentos/competências, verificando assim se as mais valias perduram no tempo. Isto é, verificando se os novos conhecimentos/competências foram realmente integrados no saber dos futuros professores.
Devido a questões de absentismo/disponibilidade dos alunos, dispomos de sete resoluções do teste diagnóstico antes do funcionamento da disciplina e de quatro resoluções realizadas um ano após a primeira apresentação do teste diagnóstico.
Questões
As questões do teste diagnóstico foram escolhidas tendo em conta a nossa experiência no ensino de disciplinas (com conteúdos de pré-cálculo e cálculo) em diversos cursos do 1º Ciclo da área de Ciências Naturais.
Na Figura 1 mostra-se a questão 5. do teste diagnóstico com a qual se pretendeu avaliar o conhecimento do conteúdo relativo à resolução de equações.

Especificamente pretendeu-se testar se o aluno tinha a preocupação de analisar (como passo inicial ou, pelo menos, como parte do processo de verificação da veracidade da sua resposta) o domínio da função
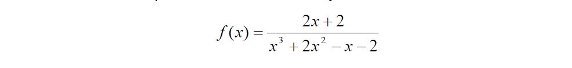
tendo em conta que um dos erros mais frequentes dos nossos alunos é considerar que as expressões de
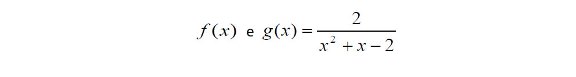
representam a mesma função. Além disso, avaliou-se a aplicação correta da Regra de Rufini.
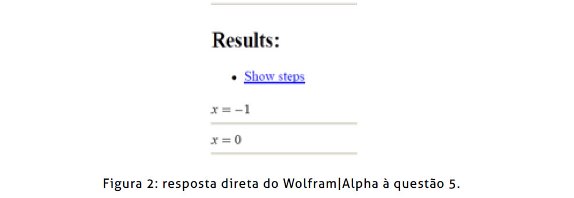
Notemos que o “site” relativo ao Wolfram|Alpha apresenta como resposta ao exercício o que se mostra na Figura 2. O utilizador só tem a informação correta quando seleciona a opção “show steps” (ver Figura 4).

Na Figura 3 mostra-se a questão 6. do teste diagnóstico. Com esta questão pretendeu-se avaliar os conhecimentos dos alunos relativamente ao conceito de função módulo e ao cálculo de limites.
Resolução
Tendo em conta que os conteúdos programáticos relativos ao pré-cálculo foram explorados com o Wolfram|Alpha, apresentamos as resoluções às questões 5. (Figura 4) e 6. (Figura 5) fornecidas por esta poderosa ferramenta.
Note-se que a resolução, à questão 6. do teste diagnóstico, apresentada pelo Wolfram|Alpha não é a mais adequada para os alunos do ensino secundário (em Portugal). Assim, a Figura 6 mostra a resolução que julgamos ser, pedagogicamente, a mais indicada para alunos deste nível de ensino.

Respostas ao teste diagnóstico
Nesta subseção apresentamos alguns dos erros cometidos pelos futuros professores em formação inicial, antes e depois da frequência à disciplina. As figuras 7, 8, 10, 13, 15, 16 e 17 são referentes a resoluções efetuadas antes do funcionamento da disciplina. As figuras 9, 11, 12 e 14 dizem respeito a respostas elaboradas já durante a prática de ensino supervisionada.






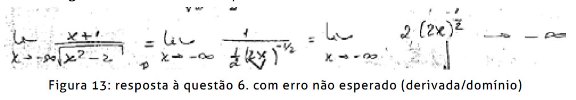




Situação 1.
As Figura 7 e Figura 8 apresentam partes de respostas de alunos, à questão 5., antes da frequência à disciplina e a Figura 9 durante a prática de ensino supervisionada. Pode-se observar que em todos os casos não existiu qualquer preocupação na análise do domínio da função f(x) sendo, no entanto, utilizadas abordagens diferentes na resolução.
Situação 2.
A Figura 10 apresenta partes da resposta de outro aluno, antes da frequência à disciplina. Pode-se observar que, além de não ter existido qualquer preocupação na análise do domínio da função f (x) , a Regra de Rufini não foi aplicada de forma correta.
A Figura 11 apresenta partes da resposta de um aluno, à questão 5., depois da frequência à disciplina. Pode-se observar que a Regra de Rufini não foi aplicada de forma correta (em dois sentidos distintos). Além disso, o aluno não teve em consideração o domínio e não foi capaz de continuar o processo de resolução.
Situação 3.
A Figura 12 apresenta parte da resposta de um aluno, à questão 5., depois da frequência à disciplina. Pode-se observar que existiu preocupação na análise do domínio das expressões envolvidas, mas falhas de rigor matemático. Apesar de ter chegado ao conjunto solução correcto foram efetuados erros no uso dos sinais de disjunção e conjunção.
Situação 4.
Nesta situação mostramos dois exemplos referentes a erros cometidos pelos futuros professores em formação inicial, na resolução da questão 6., não previstos aquando da elaboração do teste diagnóstico. A Figura 13 apresenta parte da resposta de um aluno, antes da frequência à disciplina, e ilustra falhas no conhecimento do conteúdo referente ao conceito de domínio de uma função real e no cálculo de derivadas, na tentativa de aplicar a Regra de Cauchy. Esta regra não só não faz parte dos atuais conteúdos programáticos do ensino secundário em Portugal, como também não permitiria calcular o limite em causa.
Por sua vez a Figura 14 mostra uma resolução, realizada após a disciplina, que apresenta um erro na aplicação da propriedade distributiva, o que elimina a possibilidade da avaliação do conhecimento do aluno relativamente ao conceito de função módulo.
Situação 5.
Nesta situação mostramos dois exemplos de resoluções que ilustram a falta de conhecimento do conteúdo sobre indeterminações do tipo  . As Figura 15 e Figura 16 apresentam partes de respostas incompletas à questão 6., realizadas antes da frequência à disciplina.
. As Figura 15 e Figura 16 apresentam partes de respostas incompletas à questão 6., realizadas antes da frequência à disciplina.
Situação 6.
Esta situação, identificada antes da frequência à disciplina, ilustra falhas no conhecimento do conteúdo relativamente ao conceito da função módulo e falta de rigor matemático.
Discussão
Observando as respostas à questão 5. do teste diagnóstico foi notório que não houve uma preocupação, essencial para futuros professores de Matemática, em verificar se as suas possíveis soluções fazem parte, de fato, do conjunto solução da referida equação. Nas resoluções apresentadas antes do funcionamento da disciplina houve apenas dois dos sete alunos que chegaram ao conjunto solução correcto, mas mesmo estes apresentaram falhas no conhecimento do vocabulário e falta de rigor matemático. Também nas resoluções realizadas após o funcionamento da disciplina se verificou que apenas dois dos quatro alunos chegaram ao conjunto solução correcto, com o mesmo tipo de falhas e falta de rigor em todas as respostas. Os erros cometidos na resolução da questão 5. do teste diagnóstico são essencialmente de três tipos: erro na aplicação da Regra de Rufini (R), a não análise do domínio das expressões envolvidas (D) e erro no uso dos sinais de disjunção/conjunção (E/OU). Codificando cada um destes três tipos de erro com os símbolos entre parêntesis, o gráfico que se segue na Figura 18 mostra a frequência relativa destes erros em sete respostas à questão 5. do teste diagnóstico, antes do funcionamento da disciplina, e também nas quatro respostas à mesma questão depois do funcionamento da disciplina.
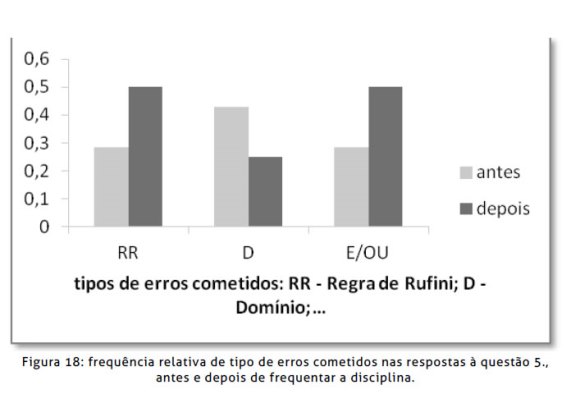
Embora a frequência relativa de erros relacionados com a análise do domínio das expressões tenha diminuído da primeira para a segunda resolução do teste diagnóstico, observou-se, na segunda resolução do teste diagnóstico, um ano após a primeira resolução, um aumento da proporção de erros quer na aplicação da Regra de Rufini, quer no uso dos sinais de disjunção/conjunção. Nas aulas da disciplina referentes à área de pré-cálculo foi dada especial atenção à análise de domínios de funções. Verifica-se que na segunda resolução do teste diagnóstico há uma maior proporção de alunos a trabalhar essa questão de forma correta, ou seja, há uma maior proporção de alunos que atinge as etapas onde deverá ser aplicada a Regra de Rufini e o uso dos sinais de disjunção e conjunção em diversas situações. Infelizmente os alunos que atingem estas eta-pas numa segunda fase de resolução do teste viram-se confrontados com novas dificuldades, aumentando a proporção destes tipos de erro.
Observando as respostas à questão 6. do teste diagnóstico foram identificadas diversas falhas no conhecimento do conteúdo (função módulo, análise de indeterminações do tipo  ). Além disso, a falta de rigor matemático revelou-se preocupante.
). Além disso, a falta de rigor matemático revelou-se preocupante.
Os erros cometidos na resolução da questão 6. do teste diagnóstico são essencialmente de três tipos: erros relacionados com conteúdos ditos mais básicos (B), como a propriedade distributiva da multiplicação relativamente à adição ou o cálculo de derivadas simples; erros inerentes à falta de conhecimento do conceito da função módulo (M) e dificuldades relacionadas com a incapacidade de tratar indeterminações do tipo  (I). Codificando cada um destes três tipos de erro/dificuldades com os símbolos entre parêntesis, o gráfico que se segue na Figura 19 mostra a frequência relativa destes erros/dificuldades em sete respostas à questão 6. do teste diagnóstico, antes do funcionamento da disciplina, e também nas quatro respostas à mesma questão depois do funcionamento da disciplina.
(I). Codificando cada um destes três tipos de erro/dificuldades com os símbolos entre parêntesis, o gráfico que se segue na Figura 19 mostra a frequência relativa destes erros/dificuldades em sete respostas à questão 6. do teste diagnóstico, antes do funcionamento da disciplina, e também nas quatro respostas à mesma questão depois do funcionamento da disciplina.
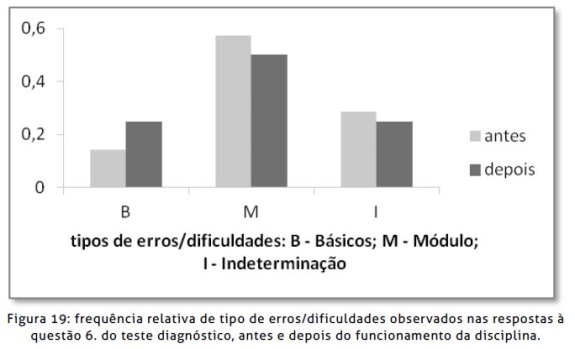
A análise das resoluções do teste diagnóstico sobre pré-cálculo antes do funcionamento da disciplina conduziu à decisão de dedicar uma especial atenção ao estudo da função módulo nas aulas. Infelizmente essa dedicação não produziu frutos visíveis uma vez que na segunda fase de resolução do teste diagnóstico continua a não existir uma única resposta correta à questão 6. Notemos que após a frequência à disciplina os alunos foram tentados a aplicar métodos alternativos (não úteis no cálculo deste limite) como a tentativa de resolução através da aplicação da Regra de Cauchy (sem erros de cálculo mas inconclusivo) e a utilização da propriedade distributiva (com erros graves na sua aplicação).
Conclusões
O número reduzido de resoluções disponíveis do teste diagnóstico, antes e depois do funcionamento da disciplina, não permite testar com significado estatístico o impacto da frequência da disciplina na melhoria do conhecimento do conteúdo de pré-cálculo destes futuros professores de Matemática.
Na criação da única disciplina da área de Matemática neste Mestrado em Ensino optámos por abordar a maioria dos temas incluídos nos conteúdos programáticos das disciplinas de Matemática no ensino secundário, nomeadamente pré-cálculo, cálculo diferencial, estatística e probabilidades e métodos de apoio à decisão. O objectivo inicial era o de dedicar a maior parte do tempo ao trabalho sobre o conhecimento específico destes conteúdos, mas dada a deficiente formação dos alunos, muito tempo foi dedicado ao conhecimento comum dos conteúdos. A inclusão de todos os temas abordados na única disciplina na área científica de docência não permitiu a dedicação necessária (dado o “background” dos alunos) a cada um dos tópicos abordados. O desfasamento entre os conteúdos lecionados no ensino superior e os conteúdos dos programas do 3º ciclo do ensino básico e do ensino secundário conduz a uma deficiente formação dos futuros professores nos conteúdos programáticos que irão lecionar.
Parece-nos pertinente a realização de um estudo mais abrangente, que permita fazer o levantamento do conhecimento dos conteúdos programáticos do ensino secundário e do 3º ciclo do ensino básico que possuem os futuros professores de Matemática, a frequentar diferentes Mestrados em Ensino em Portugal. Tal estudo permitirá tirar conclusões sobre a necessidade de incluir nestes mestrados disciplinas dedicadas ao conhecimento dos conteúdos a lecionar nos níveis de ensino para que conferem a habilitação para a docência. Ou, em alternativa incluir estas disciplinas, como opção, nas Licenciaturas em Matemática. A aferição da formação dos licenciados pós-Bolonha será um primeiro passo para conceber Mestrados em Ensino que atinjam o objectivo de formar professores possuidores de sólido conhecimento científico e com competências necessárias ao exercício da profissão.
Agradecimentos
Agradecemos à Professora Nélia Amado preciosos comentários à redação deste artigo. Agradecemos aos Professores Marielba Zacarias e Luís Bom a ajuda prestada na tradução do resumo para espanhol e francês, respetivamente.
Referências Bibliográficas
Conceição, C., Sousa, O. (2012). Ser professor hoje. O que pensam os professores das suas competências. Revista Lusófona de Educação, 20, 81-98. [ Links ]
Ball, D. L., Thames, M. H. & Phelps, G. (2008). Content knowledge for teaching: What makes it special. Journal of Teacher Education, 59 (5), 389-407. [ Links ]
Hodge, A. M., Gerberry, C. V., Moss, E. R. & Staples M. E. (2010). Purposes and perceptions: What do universitary mathematics professors see as their role in the education of secondary mathematics teachers?. PRIMUS, 20 (8), 646-663. [ Links ]
Perrenoud, P. (1999). Dix nouvelles compétences pour enseigner Invitation au voyage. Paris: ESF Éditeur. [ Links ]
Rocha, L. (2006). A formação inicial de professores no quadro do processo de Bolonha. Modelos e desafios. Revista Lusófona de Educação, 7, 165-166. [ Links ]
Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15 (2), 4-14. [ Links ]
Shulman, L.S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22. [ Links ]
Wilburne, J., Long, M. (2010). Secondary pre-service teachers’ content knowledge for state assessments: Implications for mathematics education programs. IUMPST: The Journal 1(Content Knowledge) [Disponível em www.k-12prep.math.ttu.edu, consultado em 21/03/2012].
Data de submissão: Dezembro de 2011
Data de Aceitação: Março de 2012
Data de Publicação: Dezembro de 2012