Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Lusófona de Educação
versão impressa ISSN 1645-7250
Rev. Lusófona de Educação no.25 Lisboa dez. 2013
Investigando a relação entre o jogo do Semáforo e os padrões
Investigating the relationship between the game Traffic Lights and patterns
Étudiant la relation entre le jeu Sémaphore et les structures
Investigando la relación entre el juego Semáforo y los patrones
Dores Ferreira*, Pedro Palhares**, Jorge Nuno Silva***
*Universidade do Minho, Instituto de Educação, CIEC, 4710-057 Braga, Portugal.
Email: doresferreira@gmail.com
**Universidade do Minho, Instituto de Educação, CIEC, 4710-057 Braga,
Portugal. Email: palhares@ie.uminho.pt
***Universidade de Lisboa, Faculdade de Ciências, CIUHCT, 1749-016 Lisboa.
Email: jnsilva@cal.berkeley.edu
RESUMO
Os jogos têm despertado o interesse de investigadores no sentido de averiguar o benefício da sua prática no desenvolvimento de capacidades. Este interesse emerge, possivelmente, das caraterísticas motivadoras do jogo em geral e do facto de determinado tipo de jogos envolverem destrezas cognitivas na sua prática. Estas caraterísticas levaram-nos a serem considerados como agentes facilitadores do processo de ensino e aprendizagem da matemática. A capacidade de identificar padrões é igualmente apontada como essencial a este processo, sendo considerada uma capacidade intrínseca à atividade matemática. Neste artigo apresentar-se-ão as etapas essenciais de um estudo conduzido junto de uma amostra de alunos do 1.º ciclo do ensino básico, envolvendo o jogo do Semáforo, bem como as principais conclusões. Como resultados principais do estudo verificámos a existência de uma relação entre a força de jogo e a capacidade de identificar padrões, tendo-se verificado também uma relação entre estas variáveis e a classificação obtida nas provas de aferição de matemática. Verificou-se, ainda, que uma turma sujeita à prática sistemática do jogo diferiu significativamente da turma de controlo.
Palavras-chave: jogos matemáticos; padrões; estudo correlacional; estudo quase-experimental
ABSTRACT
Games have been triggering researcher’s interest to verify whether their practice brings benefits to the development of abilities. This interest emerges, probably, from the motivating characteristics of playing in general and from the fact that certain types of games involve cognitive skills during practice. These characteristics took them to be considered facilitating agents of mathematics teaching and learning. The ability to identify patterns is equally viewed as essential to this process, as it is considered as intrinsic to mathematics activity. In this paper we will present the major steps of a study conducted within a sample of primary school students, involving the game ‘Traffic Lights’, as well as some results. As major results from this study, we have verified the existence of a relationship between strength of play and the ability to identify patterns. We have also verified the existence of a relationship between these variables and the grades obtained on the national exams in mathematics. We have also found that one class subjected to the game systematic practice has differed significantly from the control group.
Keywords: Mathematical games; patterns; co-relational study; quasi-experimental study
RÉSUMÉ
Les jeux ont attiré l’intérêt des chercheurs pour déterminer s’il n’y a aucun bénéfice de sa pratique en matière de développement des capacités. Cet intérêt apparaît peut-être motivé par les caractéristiques du jeu en général et du fait que certains types de jeux impliquent des compétences cognitives dans sa pratique. Ces faits ont conduit à que beaucoup de gens les considèrent comme des facilitateurs pour l’enseignement des mathématiques. La capacité à identifier des régularités est également impliquée comme essentielle à ce processus, étant considérée comme une capacité intrinsèque à l’activité mathématique. Cet article présente les étapes essentielles d’une étude menée auprès d’un échantillon d’élèves du 1er Cycle de l’enseignement fondamental, concernant le jeu Sémaphore, bien comme les principales conclusions. On a constaté l’existence d’une relation entre la force de jeu et la capacité d’identifier les régularités, et on a également observé une relation entre ces variables et les résultats obtenus dans les tests officiels en mathématiques. On a aussi constaté que le groupe soumis à la pratique systématique du jeu diffère de manière significative du groupe de contrôle.
Mots-clés: jeux mathématiques; étude corrélationnelle ; étude quasi-expérimentale
RESUMEN
Los juegos han atraído el interés de los investigadores con el fin de determinar el beneficio de su práctica en el desarrollo de capacidades. Este interés surge posiblemente de las características motivadoras del juego en general y el hecho de que ciertos tipos de juegos implican habilidades cognitivas en su práctica.
Estas características nos llevan a considerar los juegos como agentes facilitadores del proceso de la enseñanza y el aprendizaje de las matemáticas. La capacidad de identificar patrones también está implicado como esencial para este proceso, y se considera la capacidad intrínseca de la actividad matemática. La capacidad de identificar los patrones también se menciona como algo esencial para este proceso, y se considera una capacidad intrínseca de la actividad matemática. Este documento presenta los pasos esenciales de un estudio realizado con una muestra de estudiantes de escuela primaria, que implica el juego Traffic Lights, así como las principales conclusiones. Como principales resultados se ha constatado la existencia de una relación entre la fuerza de juego y la capacidad de identificar los patrones, y ha habido también una relación entre estas variables y las calificaciones obtenidas en las pruebas de medición de las matemáticas. También se encontró que una clase sujeta a la práctica sistemática de juego difería significativamente de la clase de control.
Palabras clave: juegos matemáticos; patrones; estudio de correlación; estudio cuasi-experimental
1. Introdução
Quando se inicia um estudo, as razões a ele subjacentes podem ser de natureza diversificada, devendo o gosto pela temática a investigar ser uma das principais. Neste caso, o gosto pessoal pelos jogos em geral foi efetivamente uma das razões principais para iniciar este estudo, aliado ao interesse em verificar as possíveis relações entre jogos e matemática, e a referência à necessidade de estudos mais abrangentes sobre jogos (Gobet, Voogt & Retschitzki, 2004).
A matemática pode ser considerada a ciência dos padrões, sendo a identificação e investigação de padrões muito úteis ao desenvolvimento da abstração e do pensamento algébrico . Estas mais-valias do estudo dos padrões são também salientadas no programa de matemática do ensino básico, de 2007, que refere, logo nos objetivos gerais, a necessidade dos alunos reconhecerem e explorarem regularidades.
Neste artigo pretende-se abordar aspetos que consideramos fundamentais no âmbito do contributo dos jogos no ensino e aprendizagem da Matemática Elementar, nomeadamente a sua relação com a identificação de padrões.
Iniciaremos com uma abordagem aos fundamentos inerentes ao estudo, seguindo-se as etapas metodológicas, dois aspetos essenciais ao seu enquadramento. Posteriormente são apresentados e discutidos os resultados, terminando com as principais conclusões e/ou reflexões finais.
2. Fundamentação teórica
Ao longo da história da humanidade, o ser humano tem revelado interesse pelo jogo, nas suas variadas dimensões. No que respeita aos jogos de tabuleiro, esse interesse é visível no grande número de artefactos encontrados em escavações arqueológicas, nomeadamente peças de jogo e tabuleiros inscritos em madeira ou pedra, que fazem parte do espólio de muitos museus. Murray (1952) refere que os jogos de tabuleiro remontam há mais de quatro mil anos, sendo exemplo disso algumas pinturas encontradas nos templos e túmulos do anti-go Egito. O facto de este tipo de jogos necessitarem de um tabuleiro facilitou o conhecimento das suas origens e existência, através da análise dos achados arqueológicos, sendo essa a principal razão para que, dos jogos antigos, os de tabuleiro sejam os que melhor se conhecem. Uma referência importante é o Livro dos jogos de Afonso X, o sábio, completado em 1283 (López, Montes, Murillo & Negro, 2010), constituindo o primeiro livro de jogos na literatura europeia.
Devido à grande variedade e complexidade de jogos, o seu estudo pode abranger áreas distintas, como a história, psicologia ou sociologia, sendo hoje em dia objeto de estudos multidisciplinares.
No âmbito da educação matemática, Bell e Cornelius (1991) propõem a investigação envolvendo diversos jogos, apresentando algumas das investigações já realizadas. Os autores consideram que, para além de os jogos constituírem uma fonte motivadora e poderem ser um ponto de partida para a resolução de problemas, promovem a utilização do pensamento lógico. Na mesma linha de pensamento, Smole, Diniz e Cândido (2007), referem que a utilização de jogos permite o desenvolvimento da observação, da reflexão, da argumentação, do raciocínio lógico e da resolução de problemas. O facto de a prática de determinados jogos contribuir para o desenvolvimento de capacidades cognitivas levaram-nos a serem considerados como agentes facilitadores do processo de ensino e aprendizagem da matemática, sendo que Palhares, Gomes e Mamede (2002) apontam para a utilização orientada de jogos, no ensino da matemática. Neto e Silva (2006) referem também o valor pedagógico dos bons jogos de tabuleiro na medida em que permitem aos jogadores “aprender a concentrar-se, a controlar o impulso da jogada rápida, a aceitar um modelo de regras fixo (aprender a separa a brincadeira do jogo), a estabelecer planos e a analisar linhas de raciocínio, a abstrair-se da parte física das peças para as considerar entes abstractos regidos por certas regras” (p. 11).
Segundo Schädler (2007), a apetência pelo jogo é mais evidente na criança, através do qual a criança ‘abre-se’ ao mundo. Atentos a este facto, os professores devem aproveitar a emotividade gerada pelo jogo para promover as aprendizagens. Krulik e Rudnick (1993) alertam para o conhecimento de que as competências adquiridas por/com prazer são mais duradouras, o que torna o jogo um bom aliado do ensino.
No âmbito da etnomatemática, Palhares (2012), refere a necessidade de se continuar a investigar o pensamento matemático envolvido na prática de jogos, bem como investigar os tabuleiros gravados na pedra de monumentos/construções anti-gas, procurando relacioná-los com o pensamento matemático dos seus construtores.
A utilização de jogos ao nível da educação matemática não é de todo novidade das últimas décadas. No séc. XI foi inventado o jogo Rithmomachia, um jogo pedagógico jogado por estudantes de aritmética, astronomia e astrologia, do qual foram publicados diversos livros (Silva, 2007). Para além de ser um jogo de números, Rithmomachia é, à semelhança do xadrez, a representação de uma batalha. Mais tarde, em 1578, aparece o Metromachia, um jogo geométrico, onde as peças do jogo são figuras geométricas utilizadas numa hierarquia em conformidade com a hierarquia militar, nomeadamente os polígonos representam a infantaria e os sólidos geométricos a cavalaria (Catarino, 2007).
Numa perspetiva inclusiva, tem vindo a ser desenvolvida uma investigação envolvendo a prática de jogos de tabuleiro por jogadores com baixa visão ou cegueira, tendo sido construídos tabuleiros adaptados para o efeito. Esta investigação tem como objetivo identificar as competências desenvolvidas por estes alunos através da prática de jogos matemáticos (Dias, Palhares & Silva, 2009).
A identificação de padrões encontra-se intrinsecamente relacionada com a matemática, sendo esta considerada a ciência que procura compreender todo o tipo de padrões, sejam os que ocorrem na natureza ou aqueles que são inventados pelo próprio ser humano (Steen, 1990).O programa de matemática aponta para a identificação e investigação de padrões numéricos e geométricos, que permitem fazer conexões entre a geometria e a aritmética, e promovem o desenvolvimento da capacidade de abstração e do pensamento algébrico. A exploração de padrões é também referida como meio para desenvolver nos alunos o seu poder matemático e ajudá-los a apreciar a beleza matemática (NCTM, 1991), sendo utilizada como uma das estratégias de resolução de problemas.
A identificação de padrões como uma atividade inerente à atividade matemática foi utilizada no âmbito de um estudo correlacional, onde se procurava identificar possíveis relações entre uma capacidade matemática e a capacidade de jogar xadrez (Ferreira & Palhares, 2008). Os resultados obtidos nesse estudo revelaram a existência de uma relação entre a força de jogo em xadrez e a capacidade de identificar padrões. A identificação desta relação entre o xadrez e os padrões, conduziu ao interesse por alargar a investigação a outro tipo de jogos.
3. Metodologia
O estudo aqui focado enquadra-se numa investigação mais ampla que abarca outros jogos. A população em estudo consiste nos alunos do 3.º ao 6.º ano de escolaridade do ensino básico português, embora no caso deste jogo de Semáforo tenha havido uma restrição ao 1.º ciclo do ensino básico.
A metodologia utilizada é de natureza quantitativa, onde se enquadram duas investigações complementares, uma de natureza correlacional e outra quase-experimental.
Cohen e Manion (1989) afirmam que a investigação correlacional em Educação é apropriada quando se pretende descobrir ou clarificar relações entre as variáveis e há pouca ou nenhuma investigação prévia sobre o assunto, na medida em que “the investigation and its outcomes may then be used as a basis for further research or as a source of additional hypotheses” (p.161).
Com a investigação correlacional pretendia verificar-se a existência ou não de relação entre a capacidade de jogar jogos matemáticos (Semáforo) e a capacidade de identificar padrões. Pretendia-se, ainda, verificar a existência ou não de relação entre a capacidade de jogar jogos matemáticos (no caso, o Semáforo) e os resultados obtidos nas provas de aferição. A recolha de dados fez-se inicialmente de forma exploratória junto dos finalistas do Campeonato Nacional de Jogos Matemáticos (CNJM). Posteriormente, foram organizados três campeonatos envolvendo respetivamente 40, 148 e 24 alunos dos 3.º e 4.º anos de escolaridade.
A capacidade de jogar foi medida através da prestação obtida (ranking) no campeonato. Na organização dos campeonatos, utilizou-se o programa Suiss Perfect para fazer os emparceiramentos.
A capacidade de identificar padrões foi medida através de um teste construído e validado por Ferreira e Palhares (2008). Trata-se de um teste constituído por 24 questões envolvendo a identificação de padrões geométricos/pictóricos e numéricos com a seguinte estrutura: a) identificar o elemento seguinte de determinado padrão; b) identificar o elemento que não se enquadra no padrão; c) produzir o elemento seguinte, ou os elementos em falta, de determinado padrão. Estas questões foram baseadas nas conclusões do estudo de Krutetskii (1976) que apontam para a existência de três tipos de abordagem: a) predominantemente lógico-verbal ou analítica; b) visual-pictórica ou geométrica e c) harmónica (que combina as duas anteriores). Os critérios de correção foram elaborados de acordo com os princípios referidos por Charles, Lester e O’Daffer (1992), em particular no ponto “Analityc Scoring Scale” (p. 30), fazendo uma analogia com o teste do estudo.
Na investigação quantitativa a seleção aleatória da amostra é essencial para garantir a validade interna da investigação. No entanto, quando se investiga em educação nem sempre é possível satisfazer essa condição, por questões de natureza prática ou ética. Os desenhos quase-experimentais revelam-se adequados quando pretendemos observar o efeito de uma intervenção educativa, tendo vantagem sobre os desenhos experimentais na medida em que ocorrem em contexto educativo natural. O desenho quase-experimental é quase um desenho experimental, onde o investigador estuda o efeito de um determinado tratamento em grupos intactos em vez de fazer a seleção aleatória dos sujeitos da amostra. Esta é a diferença mais importante, referida por Cohen e Manion (1989), entre a investigação experimental e quase-experimental.
Como pretendíamos trabalhar com grupos intactos, a nossa opção foi utilizar
a) o desenho quase-experimental. Neste desenho, considerámos que a análise apropriada seria a análise da covariância (ANCOVA), uma vez que pretendíamos estudar
b) o efeito de dois tratamentos diferentes, na capacidade de identificar padrões. A ANCOVA permitiu-nos fazer a comparação entre os resultados obtidos no pós-teste, de cada uma das turmas experimentais, com os resultados obtidos pela turma de controlo, nesse mesmo teste, controlando os efeitos do pré-teste (covariável).
Com a investigação quase-experimental pretendíamos verificar se a) a resolução de problemas em contexto de jogo e b) a prática sistemática de jogos de estratégia, melhoram a capacidade de identificar padrões nos alunos do 4.º ano de escolaridade.
Neste estudo os grupos intactos são constituídos pelas turmas. Foram utilizadas três turmas do 4.º ano de escolaridade de um agrupamento de escolas do ensino público português. As turmas foram selecionadas aleatoriamente entre as turmas de 4.º ano existentes nesse agrupamento. Também de forma aleatória, considerou-se uma das turmas como turma de controlo e as restantes constituíram as turmas experimentais. Estas turmas experimentais foram sujeitas a tratamentos distintos: a) resolução de problemas em contexto de jogo do Semáforo; b) prática do jogo do Semáforo. Assim, estávamos perante um desenho de três grupos não equivalentes sujeitos a um pré-teste e um pós-teste, sendo dois deles alvo de aplicação experimental. O pré-teste e o pós-teste correspondem ao mesmo teste, apenas aplicado em momentos diferentes. Para o grupo cujo tratamento era a resolução de problemas foi produzida uma série de 20 problemas, baseados nos problemas produzidos por Carvalho e Santos (2007) no âmbito do CNJM.
Na análise estatística foi utilizado o programa SPSS, para Windows, sendo utilizados os testes estatísticos adequados a cada tipo de investigação.
4. O jogo
O jogo do Semáforo (Traffic Lights, na versão original) é um jogo de tabuleiro inventado por Alan Parr em 1998 (Neto & Silva, 2004). O Semáforo joga-se com peças amarelas, verdes e vermelhas num tabuleiro retangular, dividido em 12 casas iguais (3 linhas por 4 colunas). As peças devem ser pelo menos 8 de cada cor.
Trata-se de um jogo para dois jogadores, que jogam alternadamente, onde em cada jogada o jogador deve fazer uma das seguintes ações:
colocar uma peça verde numa casa vazia;
substituir uma peça verde do tabuleiro por uma peça amarela;
substituir uma peça amarela do tabuleiro por uma peça vermelha. O objetivo do jogo é ser o primeiro a conseguir três peças da mesma cor em linha, na horizontal, vertical ou diagonal.
Trata-se de um jogo de estratégia com regras simples e rápido de jogar, o que é favorável para o ensino do jogo a crianças. No entanto, é um jogo que requer alguma precisão de cálculo, na medida em que a vitória depende do número de movimentos disponíveis a cada jogador até se conseguir formar uma posição que dê três em linha. O primeiro jogador que conseguir entender qual a sequência de movimentos que conduz a essa posição será o vencedor.
5. Investigação correlacional
Nesta fase do estudo, procedeu-se à recolha de dados junto de alunos dos 3.º e 4.º anos de escolaridade, com a finalidade de verificar se a capacidade de jogar Semáforo estaria ou não relacionada com a capacidade de identificar padrões. Inicialmente recolheram-se os dados junto dos finalistas do Campeonato de Jogos Matemáticos, a um total de 10 alunos. Na análise estatística recorreu-se ao coeficiente de correlação de Pearson (r) para verificar o tipo de relação existente entre as variáveis, fazendo a interpretação dos resultados de acordo com os critérios referidos na literatura. Assim, considerou-se que coeficientes entre 0,2 e 0,35 revelam uma pequena relação entre as variáveis, podendo ter alguma importância em investigação exploratória; coeficientes entre 0,35 e 0,65 revelam uma relação moderada entre as variáveis que permite previsões de grupo, sendo necessário o valor de pelo menos 0,5 para previsões individuais; coeficientes entre 0,65 e 0,85 revelam uma forte relação entre as variáveis; coeficientes acima de 0,85 revelam uma relação muito forte entre as variáveis (Cohen & Manion, 1989; Fraenkel & Wallen, 1990).
Após o tratamento e análise dos dados verificou-se a existência de uma forte relação significativa (r = -0,757, p < 0,05) entre a capacidade de jogar Semáforo e a capacidade de identificar padrões (Ferreira, Palhares & Silva, 2008) (Tabela 1). O coeficiente negativo é explicado pelo facto de as variáveis terem uma direção contrária. No caso do ranking dos jogadores, quanto maior for o número, pior posição ocupa o jogador e no caso do teste, quanto maior for o número, melhor é o aluno a identificar padrões.

Os resultados obtidos nesta análise, embora satisfatórios, foram obtidos com um pequeno número de alunos, pelo que se tornou imperativo recolher novos dados junto de uma maior amostra de alunos. Para o efeito, organizou-se um campeonato envolvendo 40 alunos. A análise estatística dos resultados revelou a existência de uma relação significativa (r = -0,316, p < 0,05) entre as variáveis em estudo (Tabela 2). Uma vez que a relação identificada foi fraca e que junto dos finalistas do CNJM a relação identificada foi forte, optou-se por fazer uma nova análise para os melhores jogadores do campeonato.

A análise estatística envolvendo os melhores jogadores de Semáforo do campeonato revelou a existência de uma forte relação significativa entre as variáveis (r = -0,808, p < 0,05).

A capacidade de identificar padrões é uma capacidade muito abrangente, podendo englobar muitas capacidades. Para averiguar as possíveis capacidades intrínsecas ao teste, foi realizada uma análise fatorial do teste (Ferreira & Palhares, 2009), envolvendo a recolha de dados a mais de 600 alunos do ensino básico. Nesta análise foram identificados sete fatores, interpretados da seguinte forma:
Fator 1 - padrões que se identificam com progressões numéricas;
Fator 2 - padrões que envolvem a repetição de três termos: ABC, ABC;
Fator 3 - padrões que envolvem simultaneamente progressões geométricas e numéricas;
Fator 4 - padrões que envolvem contagens;
Fator 5 - padrões que envolvem a identificação de números pares e ímpares;
Fator 6 - padrões onde está presente uma rotação;
Fator 7 - padrões que envolvem mais do que uma lei de formação.
Tendo entretanto recolhido dados a um total de três campeonatos, envolvendo 148 alunos dos 3.º e 4.º anos de escolaridade, realizou-se a análise estatística dos dados em função dos fatores acima identificados. Nesta análise procurou identificar-se a existência de relação entre a capacidade de jogar bem Semáforo (os melhores jogadores) e os sete fatores. Para o efeito, foi utilizado o coeficiente de Kendall’s Tau (τ), uma vez que é indicado quando há muitos empates (Field, 2009). Os resultados da análise revelaram a existência de uma relação significativa entre a capacidade de jogar bem Semáforo e o Fator 2 (τ = -0,549, p < 0,05). Posteriormente, analisou-se o grupo dos piores jogadores e aí verificou-se a existência de uma relação significativa entre o Fator 5 e a capacidade de jogar Semáforo (τ = 0,324, p < 0,05), embora pequena. Nesta análise as variáveis têm a mesma direção (os jogadores foram ordenados do pior para o melhor), pelo que não seriam esperados coeficientes negativos. No âmbito de uma investigação quase-experimental, organizou-se um novo campeonato de Semáforo, com 24 alunos do 4.º ano de escolaridade, onde competiram todos os alunos entre si. A análise estatística dos dados recolhidos permitiu verificar a existência de uma relação significativa entre a capacidade de jogar semáforo e a capacidade de identificar padrões (r = -0,486, p < 0,05).
Atendendo a que estes alunos efetuaram provas de aferição, fez-se a recolha de dados dos resultados obtidos pelos alunos na prova de aferição de matemática, com o objetivo de verificar a existência de relação entre a capacidade de jogar Semáforo e os resultados obtidos na referida prova. Nesta análise recorreu-se novamente ao coeficiente de Kendall’s Tau (τ), uma vez que os resultados das provas de aferição têm muitos empates. Os resultados da análise estatística revelaram a existência de uma relação significativa entre a capacidade de jogar Semáforo e os resultados globais das provas de aferição de matemática (τ = -0,486, p < 0,01).
Nos resultados das provas de aferição acima referidas, para além de haver a classificação global da prova, havia também a classificação por temas, nomeadamente Números e Cálculo, Geometria e Medida, Estatística e Probabilidades e Álgebra e Funções. A análise tendo em consideração cada um destes temas revelou os seguintes resultados:
relação significativa entre a capacidade de jogar Semáforo e o tema Números e Cálculo (τ= -0,448, p < 0,01);
relação significativa entre a capacidade de jogar Semáforo e o tema Geometria e Medida (τ= -0,428, p < 0,05);
relação significativa entre a capacidade de jogar Semáforo e o tema Álgebra e Funções (τ= -0,431, p < 0,05).
Com o tema Estatística e Probabilidades a relação identificada não era significativa pelo que não foi considerada. No estudo apenas têm sido consideradas as relações cujo nível de significância seja inferior a 0,05 (Field, 2009). Também se verificou a existência de uma relação significativa entre os resultados do teste e os resultados da prova de aferição de matemática (τ = 0,349, p < 0,01).
5.1. Discussão dos resultados
A capacidade de jogar Semáforo revelou estar relacionada com a capacidade de identificar padrões, junto de alunos dos 3.º e 4.º anos de escolaridade, evidenciando um maior coeficiente de correlação para o grupo constituído apenas por alunos do 4.º ano. Também se verificou que essa relação é muito mais forte no grupo de melhores jogadores. Nas análises realizadas com grupos de melhores jogadores os coeficientes de correlação foram superiores a 0,75, revelando uma relação forte entre as variáveis. Como o grupo de melhores jogadores é sempre um grupo constituído por poucos alunos, seria desejável mais investigação com mais grupos. No entanto, as análises realizadas até ao momento revelam consistência nos resultados.
Atendendo aos resultados obtidos podemos dizer que para estes alunos, quanto melhor é um aluno a jogar Semáforo, melhor será a identificar padrões. Relativamente ao grupo de melhores jogadores, os resultados do estudo também sugerem de forma mais particular que quanto melhor for o jogador, melhor será a identificar padrões repetitivos, que envolvem a repetição de três termos. Esta relação poderá ser explicada pelas caraterísticas intrínsecas ao próprio jogo, nomeadamente o facto de utilizar três cores, três peças em linha e três regras para a colocação das peças. Ao interiorizar estes agrupamentos presentes no jogo, os alunos podem desenvolver maior apetência para identificarem a unidade que se repete nos padrões repetitivos presentes no teste, uma vez que esta unidade é também constituída por três elementos. Estas caraterísticas aliadas a estratégias de jogo podem desenvolver nos alunos uma maior apetência para identificar padrões repetitivos.
No grupo de piores jogadores de Semáforo, verificou-se a existência de uma relação entre a capacidade de jogar e a capacidade de identificar padrões que envolvam números pares ou ímpares. Esta relação revela que no grupo dos piores jogadores de Semáforo quanto menor é o sucesso no jogo, menor é o sucesso na identificação de padrões que envolvem questões de paridade. Neto e Silva (2004) referem que a vitória ou derrota do jogo depende do número de movimentos disponíveis ao jogadores, sendo determinante o facto de esse número ser par ou ímpar. A relação identificada entre os piores jogadores de Semáforo e o fator 5 (números pares e ímpares) pode ser explicada pela particularidade da contagem de movimentos disponíveis estar também condicionada pela paridade.
6. Investigação quase-experimental
Após a realização da investigação correlacional, e atendendo às relações identificadas, surgiu o interesse em verificar se haveria diferenças entre a prática sistemática do jogo de Semáforo (Jogo-Semáforo) e a resolução de problemas em contexto (Problemas-Semáforo) desse mesmo jogo. Para o efeito utilizou-se uma amostra constituída por 73 alunos, pertencendo 24 à turma de controlo (controlo), 24 à turma sujeita ao tratamento de resolução de problemas em contexto de jogo (Problemas-Semáforo) e 25 à turma sujeita à prática sistemática do jogo (Jogo-Semáforo). As turmas experimentais foram submetidas a 13 sessões, com a duração de 45 min cada, que decorreram durante aproximadamente três meses, entre janeiro e março.
Ao longo das sessões, o grupo sujeito à prática sistemática do jogo de Semáforo aprendeu e praticou o jogo, após o que se organizou um campeonato. O grupo sujeito à resolução de problemas resolveu um total de 14 problemas. Na primeira e na última sessão foi passado o teste a todas as turmas, respetivamente designados de pré-teste e pós-teste.
Como se pretendia verificar se existiam diferenças significativas entre os resultados obtidos no pós-teste das turmas, controlando o efeito do pré-teste, recorreu-se à análise da covariância (ANCOVA). Esta análise permitiu verificar o efeito do fator grupo na variável dependente (pós-teste) controlando o efeito da variável pré-teste (covariável).
A ANCOVA requer que sejam cumpridos determinados pressupostos, nomeadamente a fiabilidade da medição da covariável; a normalidade das distribuições; a homogeneidade das variâncias; a existência de uma relação linear entre a covariável (pré-teste) e a variável dependente (pós-teste); a homogeneidade das retas de regressão (Field, 2009). Antes de procedermos à análise da covariância verificou-se cada um dos pressupostos, que se revelaram válidos, como explicaremos de seguida.
O primeiro pressuposto acima mencionado refere-se à fiabilidade da medição da covariável, ou seja do teste aplicado. Como já foi referido, o teste utilizado neste estudo já havia sido validado (Ferreira & Palhares, 2008). A fiabilidade foi medida através do coeficiente Alpha de Cronbach, que mede a consistência interna entre os itens. O teste obteve um valor de 0,763, que se encontra dentro dos valores aceitáveis, na medida em que deveria ser superior a 0,70 (Fraenkel & Wallen, 1990).
Para verificar a normalidade das distribuições recorreu-se aos testes de Kolmogorov-Smirnov e Shapiro-Wilk.
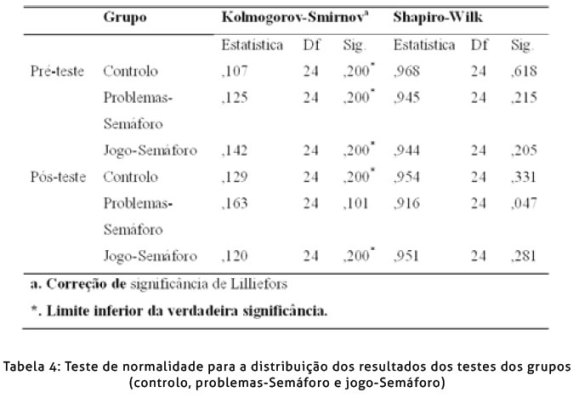
Efetuada a análise da normalidade, verificou-se que o pré-teste e o pós-teste apresentavam, em todos os grupos, um nível de significância superior a 0,05 (p > 0,05), o que revela que as distribuições não são significativamente diferentes da distribuição normal. Mantém-se, assim o pressuposto da normalidade.
O teste de Levene foi utilizado para testar a homogeneidade das variâncias entre os grupos, na variável pós-teste.

A análise dos resultados do teste revela que F (2,69) = 0,374 e p > 0,05, pelo que as variâncias não são significativamente diferentes entre os grupos.
Para verificar a linearidade entre o pré-teste (covariável) e o pós-teste (variável dependente) em cada grupo recorreu-se ao coeficiente de correlação de Pearson (r).

Os coeficientes de correlação obtidos para o grupo de controlo, o grupo Problemas-Semáforo e o grupo Jogo-Semáforo foram respetivamente r = 0,614, p < 0,01; r = 0,679, p < 0,01; r = 0,660, p < 0,01. Estes resultados revelam que existe uma relação linear estatisticamente significativa entre o pré-teste e o pós-teste de todos os grupos.
Finalmente, testamos a homogeneidade das retas de regressão para verificar se a interação entre a covariável e o fator (grupo) era significativa.
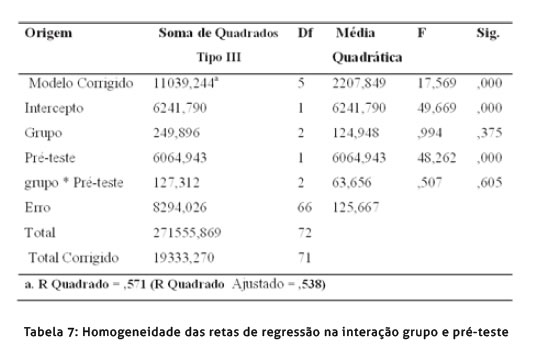
A análise da homogeneidade das retas de regressão revelou não existir uma interação significativa entre os resultados do pré-teste e o grupo (F (2,66) = 0,507, p > 0,05). Desta forma mantém-se o pressuposto.
Verificados os pressupostos foi conduzida a análise da covariância para verificar a existência de diferenças significativas entre os grupos.

A análise da covariância revelou a existência de diferenças significativas entre os grupos, sendo F (2,68) = 6,860 e p < 0,01. Com este resultado constatámos que existem pelo menos dois grupos em que a prestação dos sujeitos no pós-teste difere significativamente.
Para verificar as diferenças entre os grupos procedeu-se à análise dos contrastes que permite comparar cada um dos grupos experimentais com o grupo de controlo. No procedimento estatístico foi especificado que o grupo problemas-Semáforo e o grupo jogo-Semáforo são respetivamente comparados com o primeiro grupo (grupo de controlo).
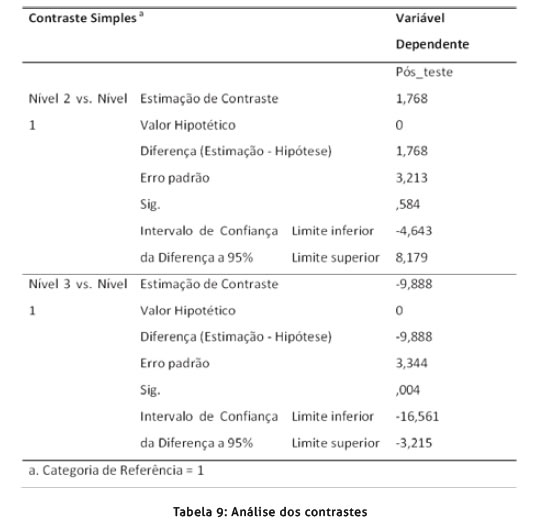
A análise dos contrastes revelou que o grupo problemas-Semáforo (nível 2) e o grupo de controlo (nível 1) não diferem significativamente (p > 0,05). Comparando o grupo jogo-Semáforo (nível 3) com o grupo de controlo verificou-se que as diferenças são significativas (p < 0,05). Como o intervalo de confiança não inclui o zero, ficámos confiantes de que as diferenças entre os grupos jogo-Semáforo e controlo são genuínas (Field, 2009).
6.1. Discussão dos resultados
Com este estudo quase-experimental pretendia-se verificar o impacto da utilização do jogo de Semáforo na capacidade de identificar padrões, tendo em consideração duas situações distintas:
resolução de problemas em contexto de jogo do Semáforo;
prática sistemática do jogo de Semáforo. Nesta parte do estudo, utilizaram-se três turmas intactas do 4.º ano de escolaridade cada uma constituindo respetivamente o grupo de controlo, o grupo de tratamento com resolução de problemas em contexto de jogo (problemas-Semáforo) e o grupo de tratamento com prática sistemática do jogo (jogo-Semáforo).
A capacidade de identificar padrões mediu-se através de um teste validado num estudo anterior (Ferreira & Palhares, 2008).
Antes de qualquer intervenção, foi aplicado o pré-teste a todas as turmas, procedendo-se de seguida ao tratamento dos dados. Posteriormente, iniciou-se o tratamento às turmas experimentais ao longo de 11 sessões, finalizando com a aplicação do pós-teste a todas as turmas. Ao todo utilizaram-se 13 sessões com a periocidade semanal e duração de aproximadamente 45 min.
Na análise estatística recorreu-se à ANCOVA por ser um procedimento adequado quando se pretende analisar as diferenças entre as médias de dois ou mais grupos, controlando a influência de uma variável identificada como covariável (Field, 2009). A variável independente grupo incluiu três níveis: controlo, problemas-Semáforo e jogo-Semáforo. A variável dependente constituiu os resultados dos alunos no pós-teste e a covariável, os resultados dos alunos no pré-teste.
A análise preliminar dos pressupostos necessários à ANCOVA revelaram que: a) a fiabilidade do teste, medida através do Alpha de Cronbach, era adequada (0,763), b) a normalidade da distribuição do pré-teste e pós-teste, medida através dos testes de Kolmogorov-Smirnov e Shapiro-Wilk, não diferem significativamente da distribuição normal (p > 0,05); o teste de Levene, utilizado para testar a homogeneidade das variâncias entre os grupos na variável pós-teste, revelou que as variâncias não são significativamente diferentes entre os grupos (F (2,69) = 0,374 e p > 0,05); o teste de Pearson, utilizado para verificar a linearidade entre o pré-teste e o pós-teste mostrou que a variável dependente e a covariável nos grupos de controlo (r = 0,614, p < 0,01), problemas-Semáforo (r = 0,679, p < 0,01) e jogo-Semáforo (r = 0,660, p < 0,01) estavam positivamente relacionadas; testou-se o pressuposto da homogeneidade das retas de regressão que confirmou não existir uma interação significativa entre os resultados do pré-teste e o grupo (F (2,66) = 0,507, p > 0,05).
A análise da covariância (ANCOVA) revelou a existência de diferenças significativas entre os grupos (F (2,68) = 6,860 e p < 0,01). Este resultado já nos sugere que há diferenças entre as turmas na prestação dos alunos a identificar padrões. No entanto, na análise dos contrastes foi possível identificar que entre o grupo jogo-Semáforo e o grupo de controlo as diferenças são significativas (p < 0,05) e a análise do intervalo de confiança permite sugerir que essas diferenças são genuínas. Este resultado sugere-nos que a identificação de padrões é significativamente diferente quando os alunos praticam sistematicamente o jogo do Semáforo.
7. Reflexões finais
A investigação correlacional permite-nos identificar a existência de relação entre determinadas variáveis, podendo as relações identificadas ser úteis para definir novas hipóteses (Cohen & Manion,1989). Na investigação correlacional realizada foram identificadas relações significativas entre a capacidade de jogar Semáforo e a) a capacidade de identificar padrões, sendo a relação muito mais forte nos melhores jogadores; b) a classificação obtida nas provas de aferição de matemática; c) a classificação obtida nos temas Números e Cálculo, Álgebra e Funções e Geometria e Medida das provas de aferição de matemática. Foi ainda identificada a existência de uma relação significativa entre o grupo de melhores jogadores de Semáforo e a capacidade de identificar padrões repetitivos, que envolvem a repetição de três termos. No grupo de piores jogadores foi identificada uma relação significativa entre a capacidade de jogar Semáforo e a capacidade de identificar padrões que envolvem noções de paridade.
Os resultados obtidos no estudo correlacional levam-nos a sugerir que incentivar os alunos a serem bons jogadores de Semáforo poderá ser uma estratégia de ensino muito útil para que esses alunos venham a ser também bons numa área específica da matemática, particularmente na identificação de padrões. Parece que o jogo de Semáforo será um bom jogo matemático para desenvolver nos alunos capacidades que são úteis no ensino e aprendizagem da matemática, nomeadamente a identificação de padrões e o conceito de paridade.
A investigação quase-experimental pode ser considerada como situando-se num ponto intermédio entre a investigação correlacional e a investigação experimental, uma vez que permite retirar conclusões ligeiramente mais consistentes do que a investigação correlacional. Com esta investigação pretendíamos verificar o impacto do jogo do Semáforo na capacidade de identificar padrões, quer na prática sistemática do jogo, quer através da resolução de problemas em contexto do jogo. Como resultado, foram identificadas diferenças significativas entre as três turmas, verificando-se que a turma sujeita à prática sistemática do jogo difere significativamente da turma de controlo. Estes resultados vieram confirmar os resultados obtidos na investigação correlacional e sugerem que há benefícios na capacidade de identificar padrões com a prática do Semáforo. Para além de serem agentes motivadores os jogos podem contribuir mais ainda para o desenvolvimento de capacidades úteis na aprendizagem da matemática.
Apesar do teste utilizado no estudo estar validado também para os alunos do 2.º ciclo, por limitações de tempo, não foi feita a recolha de dados junto destes alunos. Assim, fica em aberto uma linha de investigação com alunos do 2.º ciclo do ensino básico, procurando a identificação de relações entre o jogo do Semáforo e os padrões, sendo interessante verificar se os resultados seriam consistentes com os obtidos neste estudo.
Atendendo aos resultados obtidos, pertinentes para a população em estudo, concluímos que seria desejável um maior investimento dos professores no incentivo da prática do jogo Semáforo nos seus alunos, bem como na sua utilização em contexto educativo.
Referências
Bell, R. & Cornelius, M. (1991). Board games round the world: A resource book for mathematical investigations. Cambridge: Cambridge University Press. [ Links ]
Carvalho, A. & Santos, C. (2007). Colectânea de artigos: Estratégias utilizadas nos jogos do 4ºcnjm (36 exercícios) [Disponível em http://ludicum.org/cnjm/4/ludus-cnjm4-brochura.pdf,consultado 3 de novembro de 2007]. [ Links ]
Catarino, I. (2007). O Metromachia, Um jogo geométrico. Boletim da Sociedade Portuguesa de Matemática, número especial, pp. 53-58. SPM. [ Links ]
Charles, R., Lester, F. & O’Daffer, P. (1992). How to evaluate progress in problem solving. E.U.A.: NCTM. Cohen, L. & Manion, L. (1989). Research Methods in Education (3rd Ed.). London: Routledge. [ Links ]
Dias, C. B., Palhares, P. & Silva, J. N. (2009). Jogos matemáticos adaptados à baixa visão ou cegueira. In Alexandra Gomes (Ed). Elementary Mathematics
Education proceedings of the 3rd Meeting (pp. 145-150). Braga: AEME.
Ferreira, D. & Palhares, P. (2008). Chess and problem solving involving patterns. The Montana Mathematics Enthusiast. Vol. 5 n. 2 & 3. pp. 249-256. [ Links ]
Ferreira, D. & Palhares, P. (2009). The ability to identify patterns. Proceedings of the Elementary Mathematics Education – 3rd (pp.209-216). Braga: AEME; University of Minho.
Ferreira, D., Palhares, P. & Silva, J. N. (2008). Padrões e jogos matemáticos. REVEMAT – Revista Electônica de Educação matemática, v3.3, pp. 30-40, UFSC.
Field, A. (2009). Discovering Statistics using SPSS for Windows. London: Sage publications. [ Links ]
Fraenkel & Wallen (1990). How to Design and Evaluate Research in Education. New York: Mc Graw-Hill. [ Links ]
Gobet, F., Voogt, A. & Retschitzki, J. (2004). Moves in Mind: the Psychology of Board games. Hove: Psychology Press. [ Links ]
Krulik, S. & Rudnik, J. A. (1993). Reasoning and problem solving: a handbook for elementary school teachers. Boston: Allyn and Bacon. [ Links ]
Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren. Chicago: Chicago University Press. [ Links ]
López, A., Montes, I., Murillo, J. & Negro, I. (2010). Patrimonio Histórico Español del Juego y del Deporte: Libro de los Juegos de Alfonso X el Sabio: Acedrex, Dados e Tablas. Las Rozas: Museo del Juego S. L. [Disponível em http://www.museodeljuego.org/_xmedia/contenidos/0000000567/docu1.pdf, consultado em 1 de março de 2012]. [ Links ]
Murray, H. J. R. (1952). A History of Board-Games other than Chess. Oxford: Clarendon Press. [ Links ]
NCTM (1991). Normas para o Currículo e a Avaliação em Matemática Escolar. Lisboa: A.P.M e I.I.E. [ Links ] Neto, J. P. & Silva, J. N. (2004). Jogos Matemáticos, Jogos Abstractos. Lisboa: Gradiva. [ Links ]
Neto, J. P. & Silva, J. N. (2006). Jogos Histórias de Família. Lisboa: Gradiva. [ Links ]
Palhares, P. (2012). Mathematics Education and Ethnomathematics. A Connection in Need of Reinforcement. REDIMAT -Journal of Research in Mathematics Education, 1 (1), 79-92. doi: 10.4471/redimat.2012.04. [ Links ]
Palhares, P., Gomes, A. & Mamede, E. (2002). A formação para o Ensino da Matemática no Pré-escolar e no 1.º Ciclo: Análise teórica e estudo de caso. In Lurdes Serrazina (Org.) A Formação para o Ensino da Matemática na educação pré-escolar e no 1.º ciclo do ensino básico (21-36). Porto: Porto Editora. [ Links ]
Schädler, U. (2007). Jeux de L’humanité. Genéve: Éditions Slatkine.
Silva, J. N. (2007). O Rithmomachia. Boletim da Sociedade Portuguesa de Matemática, número especial, pp. 105-121. SPM. [ Links ]
Smole, K. S., Diniz, M. I. & Cândido, P. (2007). Jogos de matemática de 1.º ao 5.º ano. Porto Alegre: Artmed. [ Links ]
Steen, L. A. (1990). On the Shoulders of Giants: New Approaches to Numeracy. Washington: National Academy Press. [ Links ]
Data de recepção: 2 de Abril de 2012
Data de avaliação: 17 de Janeiro de 2013
Data de publicação (aceitação final): 22 de Outubro de 2013