Modelação computacional, ambientes interactivos e o ensino da Ciência, Tecnologia, Engenharia e Matemática

Computational modelling, interactive environments and Science, Technology, Engineering and Mathematics education

Modélisation computationnelle, environnements interactifs et l’enseignement de la Science, Technologie, Ingénierie et Mathématique

Modelización computacional, ambientes interactivos y la enseñanza de la Ciencia, Tecnología, Ingeniería y Matemática

 

Rui Gomes Neves* & Vítor Duarte Teodoro**

*Professor na Universidade Nova de Lisboa (UNL), Faculdade de Ciências e Tecnologia (FCT), Departamento de Ciências Sociais Aplicadas (DCSA), Unidade de Investigação Educação e Desenvolvimento (UIED). Email: rgn@fct.unl.pt

**Professor na Universidade na Universidade Nova de Lisboa (UNL), Faculdade de Ciências e Tecnologia (FCT), Departamento de Ciências Sociais Aplicadas (DCSA), Unidade de Investigação Educação e Desenvolvimento (UIED). Email: vdt@fct.unl.pt

 

RESUMO

Nas diversas áreas da Ciência, Tecnologia, Engenharia e Matemática a construção de conhecimento envolve processos de investigação baseados em acções de modelação que equilibram elementos teóricos, experimentais e computacionais. Os correspondentes ambientes, currículos e recursos de aprendizagem devem por isso estruturar-se em torno de metodologias pedagógicas baseadas nos processos de investigação profissionais, definindo estratégias específicas para cada área que sejam capazes de ajudar a estabelecer caminhos de aprendizagem epistemologicamente equilibrados através das diferentes fases cognitivas associadas aos vários tipos de processos de modelação. Este equilíbrio epistemológico-cognitivo continua, no entanto, longe de ser uma realidade para a maioria dos cursos, em particular no que se refere à integração de temas computacionais. Neste artigo discutimos uma estratégia de solução para este problema que se baseia no desenvolvimento de actividades de aprendizagem interactivas que equilibram a inclusão de experiências de modelação computacional exploratórias e expressivas. Ilustramos com exemplos de Física criados no ambiente Modellus, que podem ser utilizados ao nível do Ensino Secundário e do Ensino Superior, quer nos programas curriculares dos estudantes quer em cursos de formação de professores. Apresentamos e discutimos também resultados da implementação desta estratégia em vários cursos universitários.

Palavras-chave: Aprendizagem e ensino; Ambientes interactivos; Modelação computacional; Física; Matemática.

 

ABSTRACT

In the diverse areas of Science, Technology, Engineering and Mathematics the construction of knowledge involves research processes based on modelling actions that balance theoretical, experimental and computational elements. The corresponding learning environments, curricula and resources should then be structured around pedagogical methodologies based on the professional research processes, defining area specific strategies able to help the establishment of epistemologically balanced learning paths through the different cognitive phases of the various types of modelling processes. This epistemological and cognitive balance remains, however, far from being a reality for the majority of courses, particularly on what concerns the integration of computational themes. In this article we discuss a strategy to approach this problem that is based on the development of interactive learning activities which balance the inclusion of exploratory and expressive computational modelling experiments. We illustrate with examples from Physics created in the Modellus environment, which can be used at Secondary and Higher University or Polytechnic Education levels, either in student curricular programs or in teacher training courses. We also present and discuss results of the implementation of this strategy in several undergraduate university courses.

Keywords: learning and teaching; interactive environments; computational modelling; Physics; Mathematics

 

RÉSUMÉ

Dans les divers domaines de la Science, Technologie, Ingénierie et Mathématique la construction de la connaissance implique des processus de recherche basés sur des actions de modélisation qui équilibrent des éléments théoriques, expérimentaux et computationnels. Les correspondants environnements d’apprentissage, programmes et ressources doivent alors être structurées autour des méthodes pédagogiques basées sur les processus de recherche professionnelle, avec la définition de stratégies spécifiques capables d’aider à l’établissement de parcours d’apprentissage épistémologiquement équilibrés à travers les différentes phases cognitives des différents types de processus de modélisation. Cet équilibre épistémologique et cognitif reste, cependant, loin d’être une réalité pour la majorité des cours, en particulier en ce qui concerne l’intégration des thèmes computationnels. Dans cet article, nous discutons d’une stratégie visant à aborder ce problème qui est basé sur le développement des activités d’apprentissage interactif qui équilibrent l’inclusion des expériences de modélisation computationnelle exploratoires et expressives. Nous illustrons avec des exemples de Physique créés dans l’environnement Modellus, qui peuvent être utilisés aux niveaux de l’enseignement Secondaire ou Supérieur, soit dans les programmes scolaires des étudiants soit dans des cours de formation des enseignants. Nous présentons et discutons aussi les résultats de l’implémentation de cette stratégie dans divers cours universitaires de premier cycle.

Mots-clés: apprentissage et enseignement; environnements interactifs; modélisation computationnelle; Physique; Mathématique.

 

RESUMEN

En las varias áreas de la Ciencia, Tecnología, Ingeniería y Matemática la construcción del conocimiento implica procesos de investigación basados en acciones de modelización que equilibran los elementos teóricos, experimentales y computacionales. Por tanto, los correspondientes ambientes, programas y recursos de aprendizaje deben estructurarse en torno de metodologías de enseñanza basadas en los procesos de investigación profesional, definiendo estrategias específicas para cada área que sean capaces de ayudar a establecer caminos de aprendizaje epistemológicamente equilibrados a través de las diferentes fases cognitivas asociadas a los varios tipos de procesos de modelización. Este equilibrio epistemológico-cognitivo continúa, sin embargo, lejos de ser una realidad para la mayoría de los cursos, en particular en el que se refiere a la integración de temas computacionales. En este artículo discutimos una estrategia de solución para este problema que se basa en el desarrollo de actividades de aprendizaje interactivas que equilibren la inclusión de experiencias de modelización computacional exploratorias y expresivas. Ilustramos con ejemplos de Física creados en el ambiente Modellus, que pueden ser utilizados al nivel de la Enseñanza Secundaria y de la Enseñanza Superior, quiere en los programas curriculares de los estudiantes quiere en cursos de formación de profesores. Presentamos y discutimos también resultados de la implementación de esta estrategia en varios cursos universitarios.

Palabras clave: aprendizaje y enseñanza; ambientes interactivos; modelización computacional; Física; Matemática

 

1. Introdução

A Ciência, a Tecnologia, a Engenharia e a Matemática (CTEM) são estruturas de conhecimento evolutivas que se encontram profundamente interligadas. Por um lado, a Ciência organiza-se em torno do progressivo desenvolvimento de hipóteses, questões e modelos, geradores de teorias, que têm um forte carácter matemático na medida em que os conceitos, leis e raciocínios científicos são representados por entidades, relações e raciocínios matemáticos. Por outro lado, as explicações e previsões da Ciência têm forçosamente de ser consistentes com os resultados de experiências fiáveis e sistemáticas, que dependem tanto do progresso tecnológico e industrial como este depende do desenvolvimento científico e matemático (Chalmers, 1999; Crump, 2002).

O desenvolvimento destas estruturas de conhecimento envolve interacções entre processos de investigação individuais e colectivos, com características específicas a cada área, onde as acções de modelação ocorrem num contexto global de equilíbrio epistemológico entre aspectos teóricos, experimentais e computacionais. Por outro lado, estas acções de modelação envolvem caminhos cíclicos que passam por diferentes fases cognitivas, a saber, descrição conceptual qualitativa em contexto, construção, exploração, interpretação e validação de modelos matemáticos, apresentação e discussão de resultados, e o desenvolvimento de aplicações generalizadoras. Neste contexto é necessário elaborar especificações declarativas e operacionais rigorosas de conceitos abstractos e das suas múltiplas interconexões (Reif, 2008), um processo que requer familiarização e reificação (Teodoro, Schwartz & Neves, 2012), elevada consistência teórico-metodológica e uma precisa relação com os referentes relevantes, quer no universo real da fenomenologia natural e tecno-industrial quer em universos matemáticos abstractos.

Naturalmente, este processo de desenvolvimento evolui a partir de estruturas de conhecimento e cognição criadas para fazer face às experiências da vida quotidiana. É no entanto claro que esta evolução não é linear e que dela não resulta uma simples alteração superficial. Com efeito, apesar de indissociavelmente relacionadas com os fenómenos do mundo real, a base primordial dos modelos mentais humanos, as estruturas de conhecimento e cognição da CTEM envolvem quadros conceptuais e metodológicos abstractos que desafiam o senso comum do conhecimento de todos os dias e tornam difíceis os correspondentes processos de ensino e aprendizagem.

Para que seja possível reflectir todas as diferentes dimensões do conhecimento científico, tecnológico-industrial e matemático, os ambientes, currículos e recursos de aprendizagem devem por isso estruturar-se em torno de metodologias pedagógicas baseadas nos processos de modelação da investigação (Hestenes, 2006; National Research Council, 1989). A aprendizagem significativa (Valadares & Moreira, 2009) deve então ocorrer quando os estudantes realizam, sempre com o acompanhamento e apoio dos professores, actividades interactivas que efectuem explorações epistemologicamente equilibradas dos ciclos de modelação.

No entanto, é um facto que, mesmo em países tecnologicamente avançados e apesar dos muitos estudos já realizados, a maior parte dos cursos não manifesta esta gama de características epistemológicas, um problema que é transversal aos níveis de Ensino Básico, Secundário e Superior. De um modo geral, estes cursos não são capazes de mostrar aos estudantes como actualmente se desenvolvem as diferentes actividades científicas, tecno-industriais e matemáticas, originando com frequência opiniões negativas que contribuem para o aumento do insucesso escolar. Um exemplo ilustrativo neste contexto são os tradicionais cursos de Física Geral que habitualmente se incluem nos dois primeiros anos dos programas curriculares do Ensino Superior. Estes cursos organizam-se em torno de aulas teóricas expositivas, aulas laboratoriais e de resolução de problemas baseadas em receitas, e envolvem programas curriculares que cobrem superficialmente muitos tópicos introdutórios de Física. Nestes cursos as taxas de sucesso nos exames são baixas e muitos estudantes acabam por conseguir passar apesar de possuírem apenas um conhecimento insuficiente e fragmentado da matéria dada (Halloun & Hestenes, 1985a, 1985b; McDermott, 1991). Para além de serem considerados difíceis, estes cursos são também bastante desmotivantes para os alunos, conduzindo a uma crescente deterioração das expectativas que têm em relação à Física (Redish, Saul & Steinberg, 1998).

Que este problema pode ser tratado implementando metodologias pedagógicas baseadas nos processos de investigação profissionais é uma expectativa que tem vindo a acumular sucessivas provas científicas em diversas áreas (Handelsman et al., 2005; McDermott & Redish, 1999; Meltzer & Thornton, 2012). Com efeito, nos vários contextos destes esforços de investigação foi possível mostrar que os processos de aprendizagem efectivamente melhoram quando os estudantes se inserem em ambientes com actividades que de uma forma aproximada recriam o envolvimento epistemológico-cognitivo das acções de investigação profissionais. Ao contrário do que tem sucedido com o ensino tradicional, que acaba por induzir aprendizagens passivas com acumulação automatizada de conhecimento fragmentado de factos ou regras, estas metodologias revelaram-se mais capazes de motivar os estudantes para processos de aprendizagem significativa de carácter interactivo e investigativo, que se mostraram mais adequados para promover o conhecimento performativo e para resolver conflitos cognitivos gerados por crenças de senso comum ou ideias científico-matemáticas incorrectas.

Um aspecto fundamental no âmbito destas metodologias pedagógicas é que desde cedo se procure equilibrar a integração de actividades de modelação computacional (Ogborn, 1994). Com efeito, nos actuais processos de investigação associados às diferentes áreas da CTEM, a modelação computacional, entendida como modelação com conhecimentos e tecnologias computacionais, é tão importante nestes processos como a modelação teórica ou experimental, pois permite acções de investigação com cada vez mais aperfeiçoadas e poderosas capacidades de cálculo, exploração, visualização, simulação e validação.

A introdução de actividades de modelação computacional focou-se inicialmente na exploração das potencialidades das linguagens de programação, como por exemplo o Fortran (Bork, 1967), o Pascal (Redish & Wilson, 1993), o Logo (Papert, 1980) e o Boxer (di Sessa, 2000). Embora esta abordagem tenha evoluído, por exemplo, para o Java (Gould, Tobochnik & Christian, 2007) e para o Python (Chabay & Sherwood, 2008), permanece um facto que exige dos estudantes conhecimentos operacionais de programação, uma tarefa que dificulta principalmente o processo de aprendizagem de matérias científicas e matemáticas. O mesmo acontece com a utilização de sistemas profissionais de computação como o Mathematica ou o Matlab. Para reduzir a carga cognitiva associada à programação, particularmente pesada nos níveis introdutórios, e assim criar condições mais favoráveis para processos de modelação exploratórios e expressivos (Bliss & Ogborn, 1989; Schwartz, 2007) foram desenvolvidos vários sistemas de modelação computacional, por exemplo, o Dynamic Modelling System (Ogborn & Wong, 1984), o Stella (Richmond, 2004), o Coach (Heck, Kadzierska & Ellermeijer, 2009), as Easy Java Simulations (EJS) (Christian & Esquembre, 2007), o Modellus (Neves, Neves & Teodoro, 2013; Teodoro & Neves, 2011) e as simulações Physlet (Christian & Belloni, 2004) e PhET (Wieman, Perkins & Adams, 2008).

Apesar dos importantes progressos realizados, o conhecimento e as tecnologias computacionais, bem como os ambientes de aprendizagem baseados na natureza epistemológica e cognitiva da investigação, não estão ainda devidamente integrados nas práticas correntes dos vários níveis de ensino das diferentes áreas da CTEM. Este é um problema que envolve desafios de desenvolvimento teórico-curricular, tecnológico e organizativo cuja resolução depende criticamente da capacidade de inovação e da sustentabilidade desses mesmos processos de inovação política, social e económica das diferentes estruturas que definem os sistemas educativos. A estratégia pedagógica e de investigação-acção que propomos, e temos procurado implementar, para melhorar esta integração baseia-se no cíclico desenvolvimento e teste de currículos com actividades de aprendizagem interactivas que equilibrem a inclusão de experiências de modelação computacional exploratória e expressiva (ver, e.g., Neves et al., 2013; Neves, Silva & Teodoro, 2010, 2011; Neves & Teodoro, 2010, 2012; Teodoro & Neves, 2011). Neste artigo apresentamos uma discussão desta estratégia e dos resultados da sua implementação, começando na Secção 2 com os principais aspectos teóricos que procuramos ter em conta e relacionam conhecimento, cognição, computadores e as aprendizagens na CTEM. Na Secção 3 discutimos os elementos metodológicos e organizativos que consideramos modelares para todas as áreas disciplinares da CTEM. Na Secção 4 ilustramos com uma sequência de exemplos no âmbito da Física criados no ambiente Modellus. Na Secção 5 apresentamos as nossas conclusões, contextualizadas nos resultados das acções implementadas em vários cursos do Ensino Superior.

 

2. Conhecimento, cognição, computadores e os processos de aprendizagem na CTEM

Como vimos, o desenvolvimento das estruturas de conhecimento da CTEM é um processo cognitivo, com aspectos particulares a cada área, que envolve interacções entre processos de investigação individuais e colectivos, onde as acções de modelação ocorrem num contexto global de equilíbrio epistemológico entre aspectos teóricos, experimentais e computacionais. Neste processo, é necessário elaborar definições operativas rigorosas de conceitos abstractos e das conexões que existem entre estes conceitos, para conseguir construir modelos ou teorias com explicações e previsões que, sem ambiguidades, sejam consistentes com experiências fiáveis e sistemáticas. Neste contexto, são fundamentais os processos de definição, interpretação e validação, que envolvem familiarização e reificação conceptual e operacional, elevada consistência teórico-metodológica e uma precisa relação com os referentes relevantes, quer no universo real da fenomenologia natural e tecno-industrial quer em universos matemáticos abstractos.

Estas estruturas de conhecimento e cognição estão assim relacionadas mas são simultaneamente muito diferentes das estruturas de senso-comum utilizadas nas acções do dia-a-dia, mesmo quando estas últimas incluem fragmentos de carácter científico, tecnológico-industrial ou matemático, como é o caso das estruturas em formação dos estudantes. Uma importante barreira cognitiva que então surge nos processos de aprendizagem resulta da necessidade de distinguir com clareza conceitos e raciocínios diferentes que só aparentemente são semelhantes. Um exemplo envolve o conceito de força, simultaneamente útil para o senso-comum e para a Física. No contexto quotidiano, força é um conceito que se refere a algo que pode causar ou impedir uma certa acção ou mudança.

Directamente relacionado com causalidade é frequentemente identificado com os conceitos de energia ou potência, e categorizado como matéria e não como processo (Gupta, Hammer & Redish, 2010). Está também relacionado com raciocínios proporcionais intuitivos do tipo mais força implica maior dano ou mais força implica menos mudança, que são exemplos de estruturas de conhecimento irredutíveis ou primitivas fenomenológicas (diSessa, 1993). No âmbito da Física também se podem encontrar as mesmas primitivas mas o conceito de força está ontologicamente associado a um processo de interacção com um significado físico-matemático preciso no contexto das leis de Newton da mecânica clássica.

Esta aparente semelhança entre muitos conceitos e raciocínios do senso comum e do conhecimento científico, tecnológico-industrial e matemático é geradora de conflitos cognitivos que são, por um lado, oportunidades de aprendizagem significativa e, por outro, quando não resolvidos, focos de persistentes dificuldades que se acumulam e fragmentam o conhecimento. O exemplo seguinte também no âmbito da Física é ilustrativo.

Num carrossel circular com 6 m de diâmetro uma criança com 10 kg senta-se a 2 m do centro. Noutro carrossel idêntico senta-se uma criança com 40 kg a 1 m do centro. Os carrosséis são postos em movimento circular uniforme com a mesma velocidade angular . Seja E₁ a energia cinética de rotação do carrossel com a criança de 10 kg e E₂ a energia cinética do carrossel com a criança de 40 kg. Se não houver dissipação de energia E₁ e E₂ são as energias que é necessário despender para colocar os sistemas em rotação com velocidade angular w. Nestas condições, qual das seguintes cinco opções é verdadeira? (1) E₁=E₂/4, (2) E₁=4E₂, (3)=E₁=E₂/2, (4) E₁=2E₂, (5)E₁=E₂. Uma linha de raciocínio de senso comum esperaria que o carrossel com a criança de 40 kg fosse mais difícil de pôr a rodar por ser mais pesado e assim ser necessária mais energia para o pôr em movimento.

No entanto, de acordo com as leis da Física esta não é a resposta correcta. Se é certo que seria de facto mais difícil empurrar o sistema mais pesado ao longo de uma linha recta, neste caso o que acontece é que é igualmente difícil pôr a rodar o carrossel nas duas situações, ou seja, E₁=E₂. Para uma pessoa que aplica a linha de raciocínio de senso comum esta situação parece paradoxal e cria um conflito cognitivo. Para resolver este conflito é necessário compreender a aplicação das leis de Newton à dinâmica das rotações, concretamente neste exemplo, saber distinguir entre massa e momento de inércia, uma grandeza que depende da massa e da distribuição da massa no interior do sistema. De notar que quando esta questão foi colocada num teste diagnóstico a 163 alunos de Física de um curso de Engenharia Informática da FCT/UNL apenas 10% respondeu correctamente, tendo a maior parte escolhido uma das respostas coerentes com a linha de raciocínio de senso comum.

É importante notar também que os conflitos cognitivos não resultam apenas de conflitos com raciocínios de senso comum. Na investigação científica, por exemplo, podem também surgir na sequência de raciocínios baseados em modelos ou teorias que não são válidas, constituindo-se então simultaneamente como barreiras e oportunidades de evolução. Por exemplo, no século XIX Maxwell desenvolveu as equações que descrevem a dinâmica clássica de campos electromagnéticos. Uma das previsões fundamentais destas equações é que a luz é uma onda electromagnética que se propaga com uma rapidez constante , na altura medida igual a cerca de 300000 km/s. Quando Hertz conseguiu produzir ondas de rádio o resultado foi interpretado como evidência experimental a favor das equações de Maxwell e da existência de um meio designado por éter onde se propagavam as ondas. Apesar dos resultados das experiências de Michelson-Morley e da descoberta das transformações de Lorentz, só depois de 1905 com o estabelecimento da teoria da relatividade de Einstein é que a crença no éter foi abandonada (Gibert, 1982). Mais tarde, porém, antes de tomar conhecimento dos resultados das observações astronómicas de Hubble em 1929, Einstein não conseguiu libertar-se da crença num universo estático e em 1917 introduziu um novo termo associado a uma constante cosmológica para impedir a expansão do espaço-tempo universal prevista pelas equações que tinha desenvolvido. Em 1931 Einstein abandonou a constante cosmológica aceitando definitivamente a expansão do universo revelada pelas observações de Hubble e pelos modelos cosmológicos propostos por Friedmann em 1922 e Lemaître em 1927. No entanto, em 1998 as equipas de Perlmutter e Riess observaram supernovas em galáxias longínquas e mostraram que o universo se encontra em expansão acelerada, renovando o interesse em modelos que envolvem a constante cosmológica (Weinberg, 2008) e no seu enquadramento no contexto das teorias de campo multidimensionais com membranas que procuram unificar a teoria da relatividade geral de Einstein com a física quântica de campos e partículas do Modelo Standard (Dine, 2007; Kubyshin, Neves & Potting, 2002; Mansfield & Neves, 1996; Neves, 1997, 2007; Neves & Vaz, 2003).

Estes exemplos mostram bem que o estabelecimento de novos conceitos, modelos ou teorias e a consequente adaptação das estruturas de conhecimento é um difícil processo cognitivo, quer no âmbito da investigação profissional quer no âmbito dos processos de aprendizagem. Este processo envolve uma progressiva familiarização, que clarifica o que é diferente e o que é comum e, simultaneamente, reificação das novas estruturas abstractas que então se encaram e manipulam como realidades cognitivas objectivas e concretas (Teodoro et al., 2012). Por outro lado, envolve também o desenvolvimento de novas metáforas ontológicas (Gupta et al., 2010), fortemente dependentes do contexto, que não só permitem sequências de raciocínio mais eficazes como também uma compreensão mais profunda de conceitos e processos.

No âmbito das acções de modelação profissionais este processo de evolução esteve sempre associado ao desenvolvimento de instrumentos científicos (Crump, 2002), como por exemplo, o microscópio, o telescópio e o computador. Os processos de aprendizagem devem por isso procurar definir estratégias de utilização destes instrumentos científicos que sejam cognitiva e epistemologicamente equilibradas, tendo em vista o acompanhamento do rápido desenvolvimento do conhecimento científico, tecnológico-industrial e matemático. Neste contexto, o computador (entendendo computador como uma designação genérica que inclui também tablets para além de todo o tipo de computadores fixos e portáteis) é um exemplo paradigmático pois é um instrumento cognitivo que tem evoluído no sentido de se tornar cada vez mais acessível à utilização individual independente e ter maior capacidade para melhorar os processos de familiarização e reificação.

Com efeito, com o crescente aperfeiçoamento de hardware e software o computador tem ganho cada vez mais capacidades para ajudar a criar ambientes de aprendizagem onde as entidades conceptuais abstractas podem ser manipuladas, operacionalizadas, concretizadas e relacionadas com os respectivos referentes, no contexto de processos que ocorrem em tempo real no ecrã (Papert, 1980). Com a introdução de métodos numéricos, o computador tem a potencialidade para evitar a excessiva e automatizada aplicação de fórmulas analíticas, e focar a aprendizagem no aprofundamento da compreensão da interconexão entre o significado qualitativo e a operacionalidade quantitativa. Com o computador e os métodos numéricos, a análise de modelos mais realistas pode ser iniciada mais cedo, quando os estudantes ainda não atingiram o nível de desenvolvimento de conhecimento e cognição adequado aos métodos analíticos relevantes. Esta análise pode assim ser apropriadamente adiada para níveis de ensino mais avançados. Por outro lado, os processos de aprendizagem podem utilizar o computador para explorar com maior eficácia diferentes representações dos modelos matemáticos, como gráficos, tabelas e simulações, permitindo processos de modelação exploratórios e expressivos (Bliss & Ogborn, 1989; Schwartz, 2007), o que juntamente com a análise de modelos mais realistas potencia uma melhor conexão qualitativa e quantitativa com os respectivos referentes, um elemento cognitivo essencial na tomada de consciência das potencialidades e relevância destes mesmos modelos. Deste modo, à semelhança do que acontece nas actividades de modelação profissionais, o computador pode actuar como um poderoso espelho intelectual para a actividade cognitiva (Schwartz, 1989), uma função que aliada à sua crescente portabilidade tem claramente o potencial para favorecer o desenvolvimento dos processos de familiarização e reificação, e consequentemente, todo o processo de aprendizagem significativa.

 

3. Modelação computacional interactiva: Metodologia e organização

Como já discutimos os processos de ensino no âmbito da CTEM devem procurar ajudar os estudantes a construir novo conhecimento através de caminhos equilibrados que passem por todas as fases relativas às epistemologias e quadros cognitivos dos vários tipos de processos de modelação profissionais. Tendo em conta este ponto de partida, a estratégia de modelação interactiva que propomos envolve a definição de currículos, recursos e ambientes de aprendizagem, específicos para cada área, que equilibrem com eficácia actividades de modelação teórica, computacional e experimental, de carácter individual e colaborativo, ao mesmo tempo que têm em atenção o conhecimento prévio e as expectativas dos estudantes. Com esta estratégia o objectivo é desenvolver entre os estudantes melhores processos de familiarização e reificação, com percepção aprofundada de consistência teórico-metodológica, conexão significativa com os referentes relevantes, capacidade de criação e utilização apropriada de metáforas ontológicas, e referências actualizadas ao contexto histórico relevante para cada área específica.

Nesta secção discutimos os principais elementos do modelo metodológico e organizativo que utilizamos e consideramos relevantes para todas as áreas disciplinares e níveis de ensino, incluindo níveis de formação de professores, no âmbito da CTEM. Este modelo baseia-se num conjunto de abordagens interactivas já testadas nos EUA (ver principalmente, e. g., Beichner et al., 2007; Crouch, Watkins, Fagen & Mazur, 2007; Mazur, 1997; McDermott, Shaffer & Rosenquist, 1996; Novak, Gavrin, Christian & Patterson, 1999). Adaptações apropriadas deverão ser consideradas em cada contexto específico.

Assim, na nossa estratégia os cursos incluem sempre componentes de âmbito teórico, computacional e experimental com programas temáticos epistemologicamente coerentes e interligados. Em todas as componentes o ambiente de aprendizagem envolve uma atmosfera de colaboração com os estudantes organizados em grupos, preferencialmente de dois ou três elementos e no máximo com oito elementos. Em cada aula os grupos trabalham numa sequência de actividades de modelação constituídas por uma selecção de problemas baseadas em documentos digitais interactivos.

Estes documentos, em formato PDF e com elementos a 2D e 3D, incluem a explicação dos conceitos e métodos fundamentais, bem como dos processos de resolução de exemplos de aplicação, recorrendo a texto, imagens, áudio e vídeo interactivos, com descrições pormenorizadas de raciocínios sequenciais.

Incluem ainda séries de problemas ou desafios para resolver com diversos graus de dificuldade. Para aumentar o nível de interactividade e promover competências de comunicação digitais, os documentos contêm também espaço livre para que os estudantes possam inserir respostas ou comentários enriquecidos com recursos multimédia. Os documentos são organizados em estrutura modular para que os módulos relevantes possam ser utilizados em vários cursos. Naturalmente, a cada curso específico corresponderá um conjunto específico de documentos, organizado pelos respectivos professores.

Em cada aula as equipas de estudantes são incentivadas a analisar, discutir e resolver os problemas propostos nas actividades por si próprios. Importa aqui frisar que os grupos não devem ser abandonados durante a exploração das actividades mas sim continuamente acompanhados e apoiados pelos professores de forma a garantir um ritmo de trabalho adequado com níveis de compreensão apropriados. Sempre que necessário incluem-se discussões globais para introduzir novos temas, manter o ritmo, esclarecer dúvidas que sejam comuns a vários grupos e para apresentações de trabalhos. De notar também que cada aula é precedida de uma fase de preparação durante a qual os estudantes fazem um trabalho de casa que é depois discutido durante a aula.

Um aspecto crucial da estratégia que propomos consiste em estabelecer uma integração epistemologicamente equilibrada do computador, tendo em conta as potencialidades que tem para melhorar o desenvolvimento dos processos de familiarização e reificação. Para que isso aconteça a utilização do computador nas actividades de modelação não se pode limitar à apresentação de textos, imagens e simulações, ou a um papel de suporte à aquisição e análise de dados. Com efeito na estratégia que defendemos, o computador deve ser utilizado como um verdadeiro instrumento cognitivo, que amplifica a capacidade cognitiva dos estudantes em actividades de modelação computacional interactivas que introduzam métodos numéricos de computação científica, evitando factores de sobrecarga cognitiva como demasiadas noções específicas de programação ou software. Estas actividades são concebidas para (1) explorar os diferentes tipos de modelação, desde a modelação exploratória à modelação expressiva, (2) re-velar e resolver conflitos cognitivos relativos a conceitos e processos da CTEM, (3) promover a manipulação das diferentes representações que se podem associar aos modelos matemáticos, (3) analisar a interconexão entre as abordagens analíticas e numéricas e (4) envolver problemas mais realistas que potenciem um contacto mais profundo entre os modelos e os respectivos referentes reais. Uma escolha criteriosa de um conjunto de ferramentas computacionais que seja adaptada à especificidade de cada curso é fundamental neste contexto. Por exemplo, no âmbito da Física e da Matemática, mas também das suas aplicações a outras áreas da CTEM como a Biomedicina e as Geociências, as acções de modelação profissionais exigem conhecimento sobre modelos físico-matemáticos avançados que são ricos em elementos computacionais. A nível introdutório, desde o ensino secundário aos dois primeiros anos do ensino superior, quando as bases de Física, Matemática e Computação ainda se estão a formar, a aprendizagem deve por isso procurar equilibrar epistemologicamente a inclusão de sequências de actividades de modelação computacional criadas com sistemas que dêem aos estudantes a oportunidade de fortalecer o conhecimento computacional e ao mesmo tempo focar a aprendizagem nos conceitos e processos científico-matemáticos relevantes.

O Modellus (ver, e.g., Neves et al., 2013; Teodoro & Neves, 2011; e também a página http://modellus.fct.unl.pt) é um sistema particularmente bem desenhado para este efeito pois apresenta o seguinte conjunto de vantagens: (1) Uma fácil e intuitiva criação de modelos matemáticos através da notação matemática usual, (2) A possibilidade de criar animações com objectos interactivos cujas propriedades matemáticas estão expressas no modelo, (3) O cálculo e visualização de quantidades matemáticas obtidas através da análise de imagens e gráficos, e (4) A possibilidade de explorar simultaneamente várias representações associadas a modelos matemáticos, como imagens, tabelas, gráficos e animações.

O Modellus permite assim desenvolver actividades de modelação computacional exploratórias e expressivas, que podem ser colaborativas e concebidas para despoletar e resolver conflitos cognitivos relativos à compreensão de conceitos científicos e matemáticos, para promover a manipulação das diferentes representações associadas aos modelos e para analisar a interconexão entre as abordagens analíticas e numéricas. As actividades de modelação com o Modellus podem também envolver problemas realistas de modo a potenciar um contacto mais profundo entre os modelos e os respectivos referentes reais, um elemento cognitivo essencial na tomada de consciência das potencialidades e relevância dos modelos, necessariamente uma representação idealizada e parcial dos seus referentes. Como sistema de modelação matemática, o Modellus está particularmente vocacionado para os níveis de ensino intermédios, correspondendo aos escalões etários entre os 14 e os 18 anos. No entanto, dependendo da área da CTEM bem como do tema específico que se pretenda abordar, actividades adequadas desenvolvidas no Modellus podem ser recursos de aprendizagem significativamente relevantes quer para alunos mais jovens, entre os 6 e os 14 anos, quer para alunos mais avançados, até ao final do 1º ciclo de estudos do ensino superior.

Num processo de aprendizagem que envolva modelação computacional é importante adquirir conhecimentos algorítmicos distinguindo o significado do algoritmo da sintaxe associada a diferentes ferramentas de modelação. Neste sentido torna-se relevante optimizar a utilização de vários sistemas de modelação computacional de uma forma que efectivamente controle a carga cognitiva associada a noções operacionais de programação e software. Um exemplo concreto envolveria a optimização da utilização do Modellus em alternância com as EJS (Christian & Esquembre, 2007), um sistema complementar relativamente ao Modellus com um nível de carga cognitiva ligeiramente maior, o Excel, particularmente útil para a análise de algoritmos e dados, e o Mathematica ou o Matlab, sistemas mais avançados já ao nível das linguagens de programação mas com vantagens em termos de computação simbólica. Nas fases conceptuais qualitativas ou semi-quantitativas as simulações Modellus e EJS podem ser complementadas com simulações Physlet (Christian & Belloni, 2004) ou PhET (Wieman et al., 2008). Nos documentos PDF incluem-se instruções detalhadas para construir exemplos de modelos computacionais nas diferentes ferramentas, e nas séries de problemas, instruções incompletas, com vários níveis de desafio.

As actividades dos cursos no âmbito da nossa abordagem devem ser baseadas em plataformas colaborativas como o Moodle, que permitem distribuir de forma fácil e rápida recursos de aprendizagem e avaliação e facilitar o apoio online ou por email fora do horário das aulas presenciais. Por seu turno, os processos de avaliação envolvem avaliação contínua individual e por equipas de trabalho que são baseadas nas actividades regulares em sala de aula, nos trabalhos de casa e nos testes ou exames em sala de aula. Os materiais de avaliação recolhidos são (1) os resultados obtidos pelos estudantes em testes criados na plataforma Moodle, (2) os trabalhos realizados pelos estudantes nos documentos PDF interactivos, quer estes sejam realizados nas aulas, durante uma actividade ou teste, ou em casa, e (3) outros trabalhos e exames regulares manuscritos. No final dos cursos os estudantes respondem a um questionário com escala de Likert para avaliar as suas opiniões sobre as aulas e actividades de modelação computacional que não conta para a nota final. Este questionário é administrado na sala de aula a todos os estudantes inscritos. Outros testes (como por exemplo os testes Force Concept Inventory (FCI) (Hestenes, Wells & Swackhamer, 1992)), questionários ou entrevistas necessários para trabalho de investigação educacional também não devem contar para a nota final e devem ser administrados criteriosamente de forma a não perturbar o normal funcionamento das aulas ou prejudicar os estudantes.

 

4. Modelação computacional interactiva: Exemplos de Física

Comecemos com um exemplo sobre movimento circular, um tema que num curso de Física Geral para estudantes de Ciências, Engenharias ou Matemática do 1º ciclo do Ensino Superior pode ser introduzido depois da abordagem de temas sobre vectores, cinemática translacional, incluindo movimento relativo, e sobre as leis de Newton, incluindo exemplos de dinâmica sem rotações que envolvam soluções analíticas e numéricas simples (Neves et al., 2011; Neves & Teodoro, 2010, 2012).

Uma partícula em movimento circular descreve uma circunferência de raio R, uma curva definida por x²+y²=R² num referencial cartesiano Oxy com a origem localizada no centro da circunferência. Neste referencial x e y são as coordenadas cartesianas do vector posição 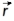. Este vector tem magnitude R e define onde a partícula se encontra na curva. Quando a partícula se move ao longo da circunferência a magnitude R permanece constante mas a direcção de 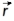varia com o tempo t. Esta direcção é definida pelo ângulo 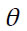que 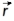faz com o eixo 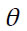x. Por definição R e 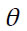são as coordenadas polares de 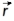. As coordenadas x e y também dependem do tempo e relacionam-se com R e 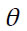através de funções trigonométricas, x=Rcos 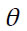, y=Rsin.

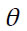A exploração dos aspectos físico-matemáticos do movimento circular deve iniciar-se com o movimento circular uniforme. Neste caso a partícula descreve uma circunferência de raio R em cada intervalo de tempo T, o período do movimento. O ângulo 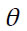é então uma função paramétrica que depende linearmente de t, 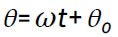onde 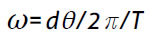é frequência angular do movimento e 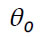é a direcção inicial de 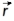. A velocidade 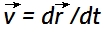é tangente à circunferência, sempre perpendicular a , e tem magnitude constante, 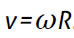. A aceleração 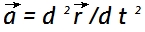tem magnitude e 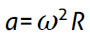é centrípeta.

Com base neste modelo trigonométrico simples os estudantes podem explorar várias actividades de modelação computacional com o Modellus (Neves et al., 2011). Para tal basta que construam um modelo matemático que associe as coordenadas x e y de 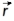às correspondentes coordenadas polares R e 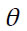, tendo em conta que 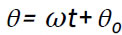. Este modelo matemático pode também incluir as coordenadas d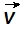e e 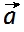, e simultaneamente pode ser complementado com gráficos e tabelas que mostrem como dependem de as diferentes coordenadas d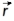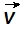e , e 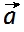, e com animações que permitem a manipulação dos parâmetros independentes R, T, e 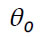e a visualização em tempo real da trajectória da partícula e dos vectores 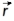, 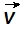e 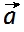(Neves et al., 2011).

Se o movimento circular for acelerado então 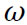já não é constante. Neste caso a magnitude da aceleração angular 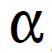define a taxa instantânea de variação de 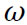com o tempo t, 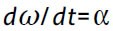. Como 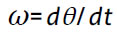temos 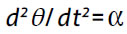. Quando 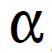é constante obtém-se então 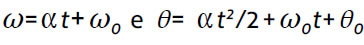. Com estas expressões d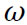e e 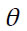os estudantes podem agora construir um modelo matemático com funções trigonométricas para descrever um movimento circular uniformemente acelerado.

Podem também complementá-lo com gráficos e tabelas das várias coordenadas d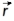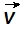e , e 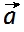com animações que permitem a manipulação dos parâmetros independentes R, 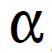, 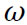₀, 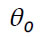, e a visualização em tempo real da trajectória da partícula e dos vectores 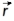, 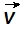e 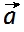. Combinando os modelos matemáticos do movimento circular uniforme e do movimento circular uniformemente acelerado, e explorando as diferentes representações simultaneamente acessíveis com o Modellus, os estudantes podem analisar uma corrida entre dois corredores.

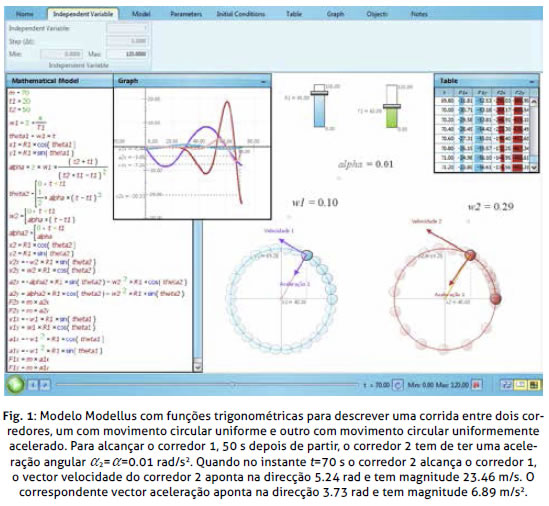
Um desafio concreto seria, por exemplo, resolver o seguinte problema (figura 1): Um corredor parte da posição (R, 0) para percorrer uma circunferência de raio R=80 m em cada 60 s. Passados 20 s, um segundo corredor parte do mesmo ponto com velocidade angular inicial nula e uma certa aceleração angular constante. Qual o valor da magnitude desta aceleração quando o primeiro corredor é alcançado 50 s depois do segundo corredor partir? Neste instante determine, para ambos os corredores, a velocidade, a aceleração e a resultante das forças aplicadas, supondo que ambos têm massa igual a 70 kg. Com esta actividade de modelação computacional interactiva os estudantes podem reforçar os conhecimentos físico-matemáticos já adquiridos sobre o movimento circular. Por exemplo, podem mostrar que no movimento circular uniformemente acelerado a velocidade continua a ser um vector tangente à trajectória agora com magnitude v=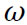R, onde 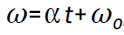, e que a aceleração passa a ter uma componente tangencial com magnitude 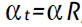, para além da componente centrípeta com magnitude 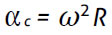(Fig. 1). Na animação do Modellus estes vectores podem ser associados a cada um dos corredores (representados por partículas) em movimento e visualizados em simultâneo com a trajectória circular (Fig. 1). Por outro lado, os gráficos de v, 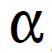e 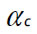em função do tempo t podem também ser desenhados em tempo real. Os estudantes têm assim a oportunidade de explorar diferentes valores dos parâmetros do modelo matemático ou de corrigir eventuais erros visualizando de imediato o efeito das alterações efectuadas na animação e nos gráficos ou tabelas.

 

 

Quando 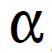não é constante a solução analítica da equação 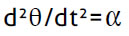pode não ser fácil de obter. Torna-se então vantajoso aplicar métodos numéricos simples como o método de Euler ou método de Euler-Cromer (ver, e.g., Neves et al., 2013; Neves et al., 2010; Neves & Teodoro, 2010, 2012). O desafio seguinte é ilustrativo neste contexto e envolve uma actividade sobre a dinâmica rotacional de um corpo rígido, numa situação em que cada partícula executa um movimento circular em torno de um eixo de rotação fixo (Neves et al., 2010). Uma barra com 1 m de comprimento roda em torno de um eixo que lhe é perpendicular e passa por uma das suas extremidades. Quando efectua 7 revoluções por segundo a energia cinética de rotação K é 2 kJ. Como w=14p rad/s o momento de inércia I é igual a 2.1 kg∙m2. Suponha que a aceleração angular da barra é dada por 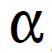(t)=-t²+3t e que no instante inicial a velocidade angular é 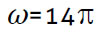rad/s. Construa um modelo que aplicando o método de Euler-Cromer permita calcular 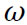(t), K(t) e 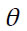(t). 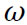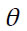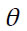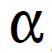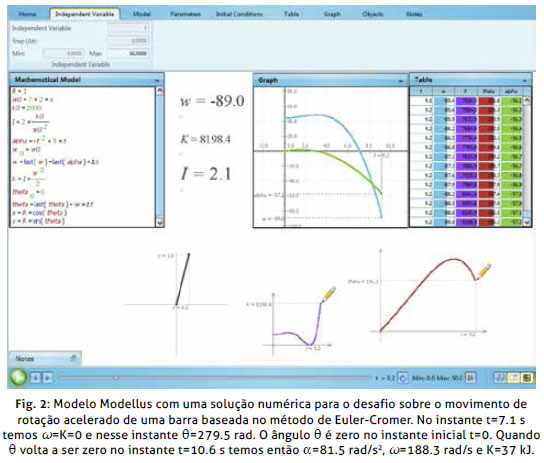Depois, utilizando os respectivos gráficos e valores tabelados, determine (1) O instante em que e K se anulam, e o valor de nesse instante, (2) O instante em que volta a ser zero, e os valores de , 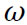e K nesse instante. A Fig. 2 mostra uma solução para este desafio que permite a exploração de valores diferentes para os parâmetros do modelo matemático bem como várias funções (t) .

 

 

5. Conclusões

Neste artigo, apresentámos uma estratégia de modelação computacional interactiva para melhorar o equilíbrio epistemológico-cognitivo dos processos de aprendizagem da CTEM, uma estratégia pedagógica e de investigação-acção que se baseia no cíclico desenvolvimento e teste de currículos com actividades de aprendizagem interactivas que equilibrem a inclusão de experiências de modelação computacional exploratória e expressiva. Como exemplos ilustrativos considerámos uma sequência de actividades de Física sobre movimento circular e dinâmica rotacional desenhada para estudantes de Ciências, Engenharias ou Matemática do 1.º ciclo do Ensino Superior.

Desde 2008, estas e outras sequências de actividades de modelação computacional interactiva criadas em ambiente Modellus foram testadas durante a implementação da nossa estratégia nos cursos de Biofísica e Física IB do Mestrado Integrado em Engenharia Biomédica e no curso de Física da Licenciatura em Engenharia Informática da FCT/UNL, bem como no curso de Meteorologia e Climatologia que envolveu estudantes de várias licenciaturas da Faculdade de Ciências e Tecnologia da Universidade do Algarve (FCT/UAlg), concretamente, Arquitectura Paisagista, Engenharia do Ambiente, Ciências do Mar e Biologia (Neves et al., 2013; Neves et al., 2010, 2011; Neves & Teodoro, 2010, 2012; Teodoro & Neves, 2011).

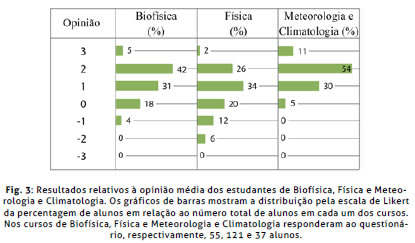
Como mostraram os resultados médios retirados dos questionários com escala de Likert, e consistentemente desde 2008, a maioria dos estudantes reagiu positivamente às actividades de modelação computacional interactiva (Fig. 3 e 4; Neves et al., 2013; Neves et al., 2011). No questionário os estudantes assinalavam a sua opinião em relação a um conjunto de afirmações, utilizando uma escala de Likert de – 3 a + 3, onde – 3 significava estar em completo desacordo e + 3 estar completamente de acordo, representando os restantes valores negativos (-2 e -1) desacordo parcial e os valores positivos (1 e 2) acordo parcial. O valor 0 significava não ter opinião preferencial. Podemos então definir a opinião média de um estudante como a média sobre todas as respostas dadas pelo estudante no questionário. Os resultados obtidos para este constructo (Fig. 3) na edição 2011/2012 do curso de Biofísica mostram que 78% dos estudantes manifestaram uma opinião positiva, com médias 1, 2 ou 3, e apenas 4% manifestaram uma opinião negativa com média -1. Os restantes 18% com média 0 não manifestaram uma opinião preferencial. Na edição 2011/2012 do curso de Física os resultados mostram que 62% dos estudantes manifestaram uma opinião positiva, com médias 1, 2 ou 3, 18% manifestaram uma opinião negativa com médias -1 ou -2, e os restantes 20% com média 0 não manifestaram uma opinião preferencial. Na edição 2011 do curso de Meteorologia e Climatologia os resultados mostraram que 95% dos estudantes manifestaram uma opinião positiva, com médias 1, 2 ou 3, 5% não tiveram opinião preferencial e nenhum aluno manifestou opinião média negativa.Por outro lado, podemos também definir a média da opinião de todos os estudantes em relação a cada uma das afirmações do questionário (Fig. 4). Os estudantes de Biofísica, e também os de Física e Física IB (Neves et al., 2011), manifestaram uma clara preferência para trabalhar em equipa num ambiente de aprendizagem interactivo e exploratório, desde que com apoio adequado dos professores. Os estudantes de Meteorologia e Climatologia já não reagiram tão favoravelmente ao trabalho de grupo (Neves et al., 2013). Embora mais estudantes continuassem a preferir o trabalho em equipa, em comparação com os cursos da FCT/UNL houve mais estudantes com preferência pelo trabalho individual.

 

 

 

 

Tendo em conta os diferentes contextos dos cursos, os estudantes consideraram o Modellus útil para o processo de aprendizagem de modelos físico-matemáticos, para a sua formação profissional e suficientemente fácil de aprender e utilizar. A apresentação das actividades de modelação computacional com o Modellus em documentos PDF interactivos com suporte vídeo integrado e espaço livre para respostas ou comentários multimédia foi igualmente considerada interessante e bem concebida. Nestes cursos o Modellus foi testado com sucesso como uma ferramenta pedagógica de modelação matemática que permite aos estudantes a exploração e construção de modelos físico-matemáticos com simulações interactivas e várias outras representações. Estes modelos podem envolver equações diferenciais resolvidas com métodos numéricos simples e os estudantes foram capazes de compreender a interconexão entre soluções analíticas e soluções numéricas. No entanto, é importante notar que os resultados dos questionários também indicam a existência de alguma cautela entre os estudantes em relação a esta nova forma de aprender Física com métodos e tecnologias computacionais.

Em todas estas acções de investigação, a análise de conteúdo dos trabalhos e testes realizados pelos estudantes mostrou que as actividades de modelação computacional foram bem-sucedidas na identificação e resolução de várias dificuldades que os estudantes tiveram em conceitos e métodos físico-matemáticos chave. Este sucesso reflectiu-se nos bons resultados obtidos pelos estudantes no final dos diferentes cursos. Por exemplo, na edição 2011/2012 do curso de Biofísica a classificação final média foi 77% na escala 0-100 e todos os 63 estudantes conseguiram completar a componente de modelação computacional. Por seu turno no curso de Física a classificação final média foi 78% e apenas 4 não tiveram aproveitamento. Na edição 2011 do curso de Meteorologia e Climatologia a classificação final média foi 70% e dos 53 estudantes inscritos apenas 3 não passaram na componente de modelação computacional.

Três factores fundamentais contribuíram para estes resultados positivos, a saber, a oportunidade de (1) efectuar modelação exploratória e expressiva, (2) ter uma correspondência visível em tempo real entre simulações com objectos com os quais se pode interagir e as propriedades matemáticas desses objectos definidas no modelo, e (3) manipular simultaneamente várias representações diferentes do modelo (o modelo matemático, a simulação, os gráficos e as tabelas).

Estes resultados constituem um inequívoco progresso em relação ao Ensino Superior tradicional. No entanto, é evidente que é necessária mais investigação (e consequentemente mais investimento que proporcione melhores condições de implementação e de aprendizagem para os estudantes) para, por exemplo, (1) melhorar o grau de equilíbrio epistemológico e cognitivo entre os aspectos teóricos, experimentais e computacionais; (2) alargar o âmbito temático das acções, quer em termos de desenvolvimento de recursos quer em termos de implementação no terreno com estudantes e professores, a outras matérias da Física (e.g., para além de outros temas de mecânica, o electromagnetismo, a termodinâmica e tópicos de física moderna como a relatividade e a mecânica quântica), da Matemática (e.g., análise matemática, métodos numéricos, álgebra, estatística e probabilidades), e das aplicações da Física e da Matemática, e.g., à Biomedicina e às Geociências; (3) aprofundar a análise da interconexão epistemológica entre a Física e a Matemática, e correspondentes implicações didácticas; (4) analisar as interacções e potencial de complementaridade de diferentes sistemas de modelação computacional, e.g., o Modellus, as EJS, o Excel, o Mathematica ou o Matlab; e (5) aprofundar a análise, quer a nível quantitativo quer a nível qualitativo, dos processos de ensino e aprendizagem, procurando mais provas científicas que mostrem que no contexto da nossa abordagem ocorre um efectivo e equilibrado desenvolvimento de conhecimento e cognição. Abordaremos estes problemas em futuras publicações.

 

Agradecimentos

Agradecemos o apoio da Unidade de Investigação Educação e Desenvolvimento (UIED), da Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa (FCT/UNL) e da Fundação para a Ciência e a Tecnologia, Ministério da Educação e Ciência (FCT/MEC), Programa Compromisso com a Ciência, Ciência 2007.

 

Referências Bibliográficas

Bork, A. (1967). Fortran for physics. Reading, MA: Addison-Wesley.         [ Links ] Chabay, R., & Sherwood, B. (2008). Computational physics in the introductory calculus-based course. American Journal of Physics 76, 307-313.         [ Links ]

Chalmers, A. (1999). What is this thing called science? London: Open University Press.         [ Links ]

Christian, W., & Belloni, M. (2004). Physlet physics: Interactive illustrations, explorations, and problems for introductory physics. Upper Saddle River, NJ: Prentice Hall.         [ Links ]

Christian, W., & Esquembre, F. (2007). Modeling physics with Easy Java Simulations. The Physics Teacher 45, 475-480.         [ Links ]

Crump, T. (2002). A brief history of science, as seen through the development of scientific instruments. London: Robinson.         [ Links ]

Dine, M. (2007). Supersymmetry and string theory: Beyond the Standard Model. Cambridge: Cambridge University Press.         [ Links ]

diSessa, A. (1993). Toward an epistemology of physics. Cognition and Instruction 10, 105–225.

diSessa, A. (2000). Changing minds: Computers, learning and literacy. Cambridge, MA: MIT Press.         [ Links ]

Gupta, A., Hammer, D., & Redish, E. (2010). The case for dynamic models of learners ontologies in physics. The Journal of the Learning Sciences 19, 285–321.

Halloun, I., & Hestenes, D. (1985a). The initial knowledge state of college students. American Journal of Physics 53, 1043-1055.         [ Links ]

Halloun, I., & Hestenes, D. (1985b). Common-sense concepts about motion. American Journal of Physics 53, 1056-1065.         [ Links ]

Handelsman, J., Ebert-May, D., Beichner, R., Bruns, P., Chang, A., DeHaan, R., Gentile, J., Lauffer, S., Stewart, J., Tilghmen, S., & Wood, W. (2005). Scientific Teaching. Science 304, 521-522.         [ Links ]

Mazur, E. (1997). Peer Instruction: A user’s manual. Upper Saddle River, NJ: Prentice Hall.

McDermott, L. (1991). Millikan Lecture 1990: What we teach and what is learned– closing the gap. American Journal of Physics 59, 301-315.

Meltzer, D., & Thornton, R. (2012). Resource Letter ALIP-1: Active-learning instruction in physics. American Journal of Physics 80, 478-496.         [ Links ]

Neves, R. (1997). D-instantons in non-critical open string theory. Physics Letters B 411, 73-78.         [ Links ]

Neves, R. (2007). Braneworlds, conformal fields and the gravitons. Journal of Physics A: Mathematical and Theoretical 40, 6991-6997.         [ Links ]

Neves, R., Neves, M. C., & Teodoro, V. (2013). Modellus: Interactive computational modelling to improve teaching of physics in the geosciences. Computers & Geosciences 56, 119-126.         [ Links ]

Neves, R., Silva, J., & Teodoro, V. (2010). Computational Modelling in Science, Technology, Engineering and Mathematics Education. In A. Araújo, A. Fernandes, A. Azevedo & J. F. Rodrigues (Eds.), Proceedings of the EIMI 2010 Conference: Educational interfaces between mathematics and industry (pp. 387-397). Bedford, MA: Centro Internacional de Matemática, Comap Inc.         [ Links ]

Neves, R., Silva, J., & Teodoro, V. (2011). Improving learning in science and mathematics with exploratory and interactive computational modelling. In

G. Kaiser, W. Blum, R. Borromeo-Ferri & G. Stillman (Eds.), International perspectives on the teaching and learning of mathematical modelling, vol. 1, ICTMA14: Trends in teaching and learning of mathematical modelling (pp. 331341). Dordrecht: Springer.

Neves, R. & Teodoro, V. (2010). Enhancing science and mathematics education with computational modelling. Journal of Mathematical Modelling and Application 1(2), 2-15.         [ Links ]

Neves, R., & Teodoro, V. (2012). Improving science and mathematics education with computational modelling in interactive engagement environments. In T. Simos, G. Psihoyios, C. Tsitouras and Z. Anastassi (Eds.), Numerical Analysis and Applied Mathematics 2012, AIP Conference Proceedings 1479, 1806-1809.         [ Links ]

Neves, R., & Vaz, C. (2003). Brane world dynamics and conformal bulk fields. Physical Review D 68, 024007-024019.         [ Links ]

Novak, G., Gavrin, A., Christian, W., & Patterson, E. (1999). Just in time teaching: Blending active learning with web technology. Reading, MA: Addison-Wesley.         [ Links ]

Papert, S. (1980). Mindstorms: Children, computers and powerful Ideas. New York: Basic Books.         [ Links ]

Redish, E., Saul, J., & Steinberg, R. (1998). Student expectations in introductory physics. American Journal of Physics 66, 212-224.         [ Links ]

Redish, E., & Wilson, J. (1993). Student programming in the introductory physics course: M.U.P.P.E.T. American Journal of Physics 61, 222-232.         [ Links ]

Reif, F. (2008). Applying cognitive science to education: thinking and learning in scientific and other complex domains. Cambridge, MA: MIT Press.         [ Links ]

Schwartz, J. (2007). Models, Simulations, and Exploratory Environments: A Tentative Taxonomy. In R. Lesh, E. Hamilton & J. Kaput (Eds.), Foundations for the future in mathematics education (pp. 161-172). Mahwah, NJ: Lawrence Erlbaum Associates.         [ Links ]

Teodoro, V., & Neves, R. (2011). Mathematical modelling in science and mathematics education. Computer Physics Communications 182, 8-10.         [ Links ]

Teodoro, V., Schwartz, J., & Neves, R. (2012). Cognitive artifacts, technology and physics learning. In N. M. Seel (Ed.), Encyclopedia of the Sciences of Learning (pp. 572-576). Dordrecht: Springer.         [ Links ]

Valadares, J., & Moreira, M. (2009). A teoria da aprendizagem significativa. Coimbra: Almedina.         [ Links ]

Weinberg, S. (2008). Cosmology. New York: Oxford University Press.         [ Links ]

Wieman, C., Perkins, K., & Adams, W. (2008). Oersted medal lecture 2007: Interactive simulations for teaching physics: what works, what doesn’t and why. American Journal of Physics 76, 393-399.

 

Data de recepção: Junho de 2013

Data de avaliação: Julho de 2013

Data de publicação: Dezembro de 2013