Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Psicologia
Print version ISSN 0874-2049
Psicologia vol.15 no.1 Lisboa Jan. 2001
Modelos de análise de redes sociais e limitações do modelo de equilíbrio estrutural de Heider
Models of social network analysis and limitations of Heider's structural equilibrium model
Luís Soczka*
*Investigador coordenador do centro Nacional de Informação Geográfica, Ministério do Ambiente e professor catedrático da Escola Superior de Altos Estudos, Instituto Miguel Torga.
RESUMO
Uma rede social é um conjunto de relações entre um número finito de actores de um sistema social interconectados por um padrão estrutural específico. A análise de redes sociais (ARS) visa compreender as ligações entre essas entidades sociais elementares que são os actores ou unidades compósitas constituidas por subgrupos de actores, e as implicações dessas ligações para a estrutura e dinâmica do sistema. Os actores de uma rede social não são necessáriamente indivíduos ou grupos informais de indivíduos, mas quaisquer elementos de um sistema social finito interconectados entre si por um qualquer padrão relacional em que haja fluxos informativos (interações, preferências ou rejeições, associações de carácter psicológico, económico ou sociológico, etc.) verificáveis. Neste artigo o autor apresenta alguns modelos básicos de análise de redes sociais, e discute as implicações do modelo de equilíbrio estrutural de Heider, apontando algumas das suas limitações metodológicas e epistemológicas.
Palavras-chave Redes sociais; modelo do equilíbrio estrutural; teoria dos grafos.
ABSTRACT
A social network is a set of relations between a finite number of actors in a social system inter-linked in a specific structural pattern. Social Network Analysis aims to describe and help to understand the links between those basic social entities, the actors, or composite units formed by subgroups of actors, and the implications of those ties to the structure and dynamics of the system. Actors, in a social network, are not necessarily individuals or groups of individuals, and they can be any kind of elements of a finite social system interconnected by a relational pattern where information exchanges take place (personal interactions, emotional preferences and rejections, psychological and sociological associations, etc.). In this paper the author discusses some basic models of social network analyis and the implications of Heider's structural equilibrium model, stressing some of methodological and epistemological shortcomes.
Uma rede social é um conjunto de relações anti-reflexivas, entre um número finito de actores de um sistema social, interconectados por um padrão estrutural específico. A análise de redes sociais (ARS) visa compreender as ligações entre essas entidades sociais elementares, que são os actores ou unidades compósitas constituídas por subgrupos de actores, e as implicações dessas ligações para a estrutura e dinâmica do sistema. Os actores de uma rede social não são necessariamente indivíduos ou grupos formais de indivíduos, mas quaisquer elementos de um sistema social finito interconectados entre si por um qualquer padrão relacional em que haja fluxos informativos (interacções, preferências ou rejeições, associações de carácter psicológico, econômico ou sociológico, etc.) verificáveis. Podem ser organizações, subconjuntos de uma mesma organização, entidades administrativas, trocas de informações entre componentes de uma rede como o SNIG, instituições, etc. Caso a rede social incida sobre uma colecção de acotres homólogos (um conjunto de crianças de uma sala de aula ou um conjunto de laboratórios de investigação científica, por exemplo), a ARS incide sobre redes unimodais; caso o que esteja em questão sejam conjuntos de actores e/ou trocas de tipo ou níveis distintos (as trocas entre o público e a rede computacional universitária, por exemplo), a ARS incide sobre redes plurimodais. Pela definição de rede social acima proposta, verifica-se que um elemento essencial é a existência de ligações relacionais entre os elementos de uma rede. Embora tradicionalmente as análises sociométricas em psicologia tenham incidido sobre as relações afectivas entre um conjunto de elementos de um grupo ou entre subgrupos, traduzidas quer através da expressão de preferências e rejeições, quer através de comportamentos directamente observáveis (Soczka, 1973,1984,1994), a definição ampla de rede social acima proposta não implica necessariamente essa restrição. Com efeito, essas ligações podem traduzir-se por uma gama variadíssima de trocas, como fluxos de informação científica numa rede universitária nacional ou internacional, as trocas comerciais entre países, ou os fluxos de mobilidade populacional entre áreas geográficas, por exemplo. Se bem que, no plano real, o conjunto de elementos de uma rede social possa ser virtualmente infinito ou tender para números de proporções astronómicas, sendo a ARS uma modelação das relações num sistema, não é possível efectuá-la sem a delimitação prática do número de actores do sistema em análise. Num universo de trocas num sistema de proporções, como o conjunto mundial dos utentes da Internet, por exemplo, revelar-se-ia impraticável proceder a uma ARS. A colecção de actores em análise tem, portanto, de possuir fronteiras bem definidas e delimitadas, embora os actuais meios computacionais permitam que o número de actores em análise ascenda por vezes à ordem dos vários milhares.
Por outro lado, verificam-se duas abordagens distintas das propriedades de uma rede social: a abordagem estrutural, mais privilegiada do ponto de vista sociológico, e incidindo sobre as características das ligações entre os actores de um sistema, e as abordagens que visam os atributos de cada actor da rede, mais privilegiadas historicamente pela psicologia. De facto, não se trata de abordagens alternativas, mas de uma deslocação do objecto de análise em cada caso: ora o sistema e as ligações estruturais entre os actores, num caso, ora os actores propriamente ditos no quadro do sistema, no outro. Em todos os casos, a ARS não é uma análise fenomenológica ou qualitativa da estrutura ou dinâmica de um grupo. Pertence à família das modelações matemáticas em ciências sociais e socorre-se exclusivamente de técnicas matemáticas.
Para esse efeito, três grandes tradições de ARS se desenvolveram desde a obra pioneira de Moreno, nos primórdios da sociometria: a) ARS suportada pela teoria dos grafos; b) sociometria estatística; c) modelação algébrica. Veremos adiante que estas linhas de abordagem não só não são compatíveis como são, no fundo, três maneiras de ler os mesmos fenómenos a partir de linguagens matemáticas distintas. Na prática, são até leituras sobrepostas dos mesmos objectos epistémicos, e o caminho de uma ARS parte sempre de uma sociomatriz, representável por um sociograma, cuja estrutura se traduz num modelo matemático (grafo, dígrafo ou hipergrafo e suas propriedades algébricas, sendo que dois grafos isomórficos apresentam as mesmas propriedades sociométricas e representam dois conjuntos sociais exactamente equivalentes do ponto de vista da ARS).
Uma sociomatriz é um conjunto de relações entre actores sociais pertenentes a um mesmo conjunto ou grupo, em que cada elemento de cada vector-linha ou vector-coluna expressa uma quantidade indicativa da qualidade ou quantidade dessa relação. Note-se que em ARS a noção de grupo não coincide com a noção de grupo sociológico ou de grupo psicológico, dado que o objecto de análise pode até nem ser constituído por adores sociais que sejam pessoas, como acima se explicitou . E mesmo quando de pessoas se trata, não se trata necessariamente de elementos de um conjunto que caiba na delimitação conceptual de grupo tradicional mente usada em psicologia. O conjunto de cidadãos que acede via Internet a um site interactivo, por exemplo, pode ser alvo de uma ARS. O que não significa que necessariamente se constituam como grupo social formal ou informal. As ma trizes sociométricas constituem matrizes de adjacência para sociogramas traduzíveis por grafos com propriedades matemáticas definidas, e existe isomorfismo entre as matrizes de adjacências e os grafos correspondentes.
Um grafo é um conjunto de nós interligados total ou parcialmente por linhas. No caso das redes sociais, um grafo é um modelo das ligações dirigidas ou não-dirigidas entre cada par de actores do sistema, representado por nós (ou vértices), sendo as relações entre eles representadas pelas linhas (ou arcos, no caso de um grafo direccional) que ligam os nós. Assim, um grafo G consiste em dois conjuntos de informação: um conjunto de nós N=(n1, n2, n3...., ng), e um conjunto de linhas L=(l1, l2, l3.. .lg)* que os conectam, ou de arcos dirigidos, se a rede consistir em relações direccionadas tais que no arco do par ordenado <nij nj>, ni→j < > nj→ni. Para cada G (N, L) é possível existirem R (r1, r2...., rg) relações entre cada par de nós, correspondendo cada uma delas a um gerador sociométrico distinto com g(g-l) entradas para cada conjunto de Lg linhas.
Dois nós <n→ np> são adjacentes se a linha ou o arco lk=(n„ n,) estiver incluída em L, sendo vazio um grafo de g nós em que L=0. Um nó é incidente com uma linha e esta incidente com o nó se este pertencer ao par de nós que a definem. Um grafo Gs é um subgrafo de G se o conjunto de nós Ns de Gs for um subconjunto do conjunto de nós N de G e o subconjunto de linhas Ls de Gs for um subconjunto de linhas L de G. Em ARS um subgrafo é gerado cada vez que o investigador atende apenas a um subconjunto dos g elementos da rede social.
Um conceito importante em ARS é o de grau dos nós de um grafo. O grau de um nó, d(n,), é o número de linhas incidentes com esse nó, ou seja, o número de nós a ele adjacentes. Numa rede social o grau de um nó representa o número de ligações directas de um actor a outro actor do sistema, sendo que
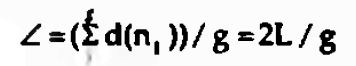
representa a expressão da media de graus nodais na rede social.
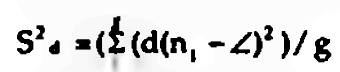
E a medida da variabilidade do grau nodal de uma rede, sendo esta uma medida importante para avaliar a centralidade de um grafo, como veremos adiante. Por outro lado, importa considerar a densidade do grafo, que avalia a proporção de linhas ou arcos existentes em relação ao número possível de linhas ou arcos, sempre relativo, como é evidente, ao número total de nós. A densidade A de um grafo é dada por
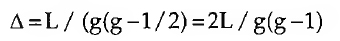
que representa uma variação de 0 (grafo vazio) a 1 (grafo totalmente conexo ou Kg). A densidade de um grafo é assim uma medida da média da proporção de linhas incidentes com os nós que compõem o grafo, dado que, sendo d=2L/g, então A=d/ (g-1). Em termos de redes sociais, A é portanto uma medida da proporção de ligações entre os actores do sistema social, o que é fundamental para proceder à avaliação da coesão dos grupos e subgrupos.
Em ARS muitas vezes lida-se com grafos dirigidos, ou dígrafos, como acima se explicitou, ou seja: distingue-se entre o emissor e o receptor da informação, sendo que uma emissão do actor ni para o actor nj na díade <ni,nj> ou m → nj não implica o caminho inverso nj→ni, constituindo-se como fenómenos independentes. Um arco é assim um par ordenado de nós de um dígrafo, o que significa que ni será adjacente a nj se <ni, nj> ∈ L. Para cada par de nós ordenados a relação pode ser nula (caso não existam arcos entre os nós), assimétrica (caso em que ni→nj mas não nj→ni) ou simétrica (reciprocidade nj↔ni).
Num dígrafo, o conceito de grau complexifica-se, desdobrando-se em I-grau e O-grau, consoante a direcção considerada do arco.1
Para o conjunto da rede,
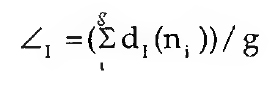
e
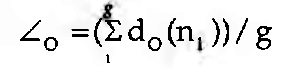
representam as médias de I-grau e O-grau da rede social, com variâncias
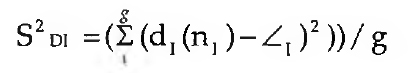
respectivamente.
Num dígrafo, um caminho é uma seqüência de arcos e nós em que cada arco tem a sua origem no nó prévio e termina no nó subsequente, tendo por comprimento o número de arcos nele contidos. Uma via é um caminho em que nenhum arco ou nó é incluído mais do que uma só vez. E uma semivia é uma sequência de nós distintos em que todos os pares de nós sucessivos são conectados por um arco do primeiro, para o segundo ou por um arco do segundo para o primeiro para todos os pares de nós sucessivos. Estes conceitos são necessários para os conceitos derivados de acessibilidade e conectividade dos elementos de uma rede social. Como se compreende intuitivamente, um nó n; diz-se acessível a partir de nj se e só se existir um caminho de nj para ni.
Um caso especial são os grafos e dígrafos sinalizados, em que os arcos ou linhas apresentam uma valência positiva ou negativa. Para a psicologia social, estes grafos apresentam um interesse particular, dados serem a base formal de um famoso modelo teórico bastante desenvolvido: o modelo de equilíbrio de Heider, a que voltaremos adiante. Mas não menos importantes são os grafos e dígrafos valorizados, ou W-grafos e W-dígrafos,2 em que a cada ligação (linha ou arco) são conferidos pesos ou medidas de intensidade (frequências de interacções, por exemplo).
Estes conceitos introdutórios conduzem-nos directamente à álgebra das relações sociais subjacente ao próprio objectivo da ARS. Uma rede social é um conjunto N de objectos (actores) interconectados. Ora, o produto cartesiano de dois conjuntos é o conjunto de todos os pares ordenados dos elementos de cada conjunto, e se N for o conjunto de actores de uma rede social, o produto cartesiano de N por si próprio dá-nos todos os pares ordenados de actores, ou seja, o conjunto de todas as díades possíveis para o conjunto N; sendo que o conjunto de relações realmente observadas é normalmente inferior ao conjunto de relações possíveis.
Partindo de uma sociomatriz X, que é, como se viu, uma matriz de adjacência de nós de um grafo, de ordem gxg, Xij=1 se os nós ni e nj forem adjacentes e Xij=0 em caso contrário. Para toda e qualquer X, xij=0. Num grafo totalmente conexo, Xij=Xji=1. Num grafo, X é evidentemente simétrica. Ora, num dígrafo, a entrada Xij não equivale necessariamente à entrada em xij. Quando tal acontece, verifica-se reciprocidade na relação social. De facto, quando X é simétrica, a sua transposta X'=X. Mas, no caso de um dígrafo, a transposição da matriz permite permutar a direcção das ligações entre pares de actores, ou seja, emissores e receptores.
Numa sociomatriz, os caminhos entre os nós de um grafo ou dígrafo são obtidos pelos produtos de X por si própria. Ou seja, pelos cálculos das n-ésimas potências de X. Seja S uma matriz simétrica derivada de X em que Sij=Sji=1 se xij=xji=1 e Sji=0 no caso contrário, sendo Sii=0. Então Xn será a césima potenciação de X e Sn a n-ésima potenciação de S. Paralelamente, xij de Xn dir-se-á xijn e sij de Sn, snij. Luce e Perry (1949) demonstraram que poderiam calcular a n-cadeias entre os elementos da matriz, em que n corresponde ao número de nós intermédios da via entre cada dois elementos, dizendo-se que a n-cadeia é redundante sempre que o mesmo elemento surge mais de uma vez na mesma cadeia. Luce (1950) definiria uma n-cadeia de ni a nj da seguinte forma:
uma n-cadeia de i a j é um conjunto ordenada de n+1 elementos, de que i é o primeiro e j o último, tal que se verifica antimetria entre i e o segundo, entre o segundo e o terceiro, etc. e entre o n-ésimo elemento e j. Se a antimetria representar comunicação, então uma n-cadeia é uma via [path] de comunicação indirecta de i para j com n passos. Duas n-cadeias são consideradas distintas uma da outra se o k-ésimo elemento da primeira difere do k-ésimo elemento da segunda nalgum valor de k entre 2 e n. Demonstrou-se que a entrada ij de xn assume um valor positivo c, isto é, xnij = c se e só se exitirem c n-cadeias distintas de i para j " (p. 170).
Efectivamente, a diagonal de X2 corresponderá ao número de relações simétricas contidas em X. Ora, S=XX', e a diagonal de S3 informar-nos-á sobre a pertença ou não de n; a um subgrupo de três elementos com relações simétricas entre si. Ou seja, aquilo a que na tradição sociométrica se designa por clique. Luce e Perry (1949) designam por clique uma cadeia de pelo menos três elementos cujas relações entre si são exclusivamente simétricas e em que o universo de elementos cujas relações são exclusivamente simétricas se encontra esgotado. Isto é: onde não há nenhum outro elemento do grupo com relações simétricas com todos os outros elementos do grupo em questão. A clique seria assim indivisível. Por definição, numa clique não existem antimetrias.3 Deste modo, um elemento i está contido numa clique se e só se a n-ésima entrada da diagonal de S3 for positiva. Se admitirmos que a coesão grupai se define justamente pela existência de ligações directas, recíprocas e fortes entre os membros de um grupo, e sabendo-se até que ponto a coesão afecta a dinâmica de um grupo, não é de estranhar a particular atenção dada a este tema desde esses tempos já recuados em que Luce e Perry (1949) e Festinger (1949) davam os primeiros passos na álgebra das relações sociais. Do ponto de vista da teoria dos grafos, uma clique é um subgrafo maximamente conexo, com exclusão de um tipo particular de subgrafos conexos: as díades em que se verifica simetria relacional. Ou seja: a tríade é considerada a base mínima de constituição de um subgrupo. No entanto, o recurso ao conceito de clique (inicialmente limitado à tríade) revelou possuir algumas limitações, umas de natureza conceptual, outras de natureza metodológica e outras ainda de natureza prática.
Talvez Luce (1950) tenha sido dos primeiros a tentar ultrapassar as primitivas limitações do conceito de clique, desenvolvendo os conceitos alternativos de n-clique e de n-conexão, que exporemos resumidamente.
Seja G(m,p) uma dada estrutura p de antimetrias definida num conjunto M de m elementos. Diz-se que G é adequadamente n-conectada se para cada par de elementos i e j existe pelo menos uma k-cadeia de i para j em que k é um inteiro positivo. Neste caso, 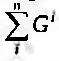 não contém entradas nulas (quando qualquer vector de G for composto apenas por zeros, G não é adequadamente conectada para nenhum valor de n). G(m,p) é exactamente n-conectada se for adequadamente n-conectada mas não exactamente k-conectada para qualquer k<n. Paralelamente, um subconjunto C para M será n-conectado se para cada par de elementos i e j em C (sendo i≠j) existir pelo menos uma k-cadeia em G(m,p) de i para j, para k<n. C será uma n-clique se e só se C for um subconjunto da estrutura G(m,p) que não seja um subconjunto de um subconjunto n-conectado de M. E Luce precisa: "Um subconjunto de uma n-clique não é uma n-clique, o que não impede que as cliques se interceptem". Para determinação das n-cliques de G(m,p) calcula-se a matriz
não contém entradas nulas (quando qualquer vector de G for composto apenas por zeros, G não é adequadamente conectada para nenhum valor de n). G(m,p) é exactamente n-conectada se for adequadamente n-conectada mas não exactamente k-conectada para qualquer k<n. Paralelamente, um subconjunto C para M será n-conectado se para cada par de elementos i e j em C (sendo i≠j) existir pelo menos uma k-cadeia em G(m,p) de i para j, para k<n. C será uma n-clique se e só se C for um subconjunto da estrutura G(m,p) que não seja um subconjunto de um subconjunto n-conectado de M. E Luce precisa: "Um subconjunto de uma n-clique não é uma n-clique, o que não impede que as cliques se interceptem". Para determinação das n-cliques de G(m,p) calcula-se a matriz 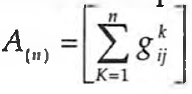 a partir da qual se obtém B(n) =[bij] onde bii=0, bii=1 se aijO e bij=0 se aij=0, para i≠j. Seja S a matriz simétrica derivada de B. Então, como anteriormente vimos, S3 dá-nos a 2-cliques de G(m,p), etc.
a partir da qual se obtém B(n) =[bij] onde bii=0, bii=1 se aijO e bij=0 se aij=0, para i≠j. Seja S a matriz simétrica derivada de B. Então, como anteriormente vimos, S3 dá-nos a 2-cliques de G(m,p), etc.
Alba (1973) propõe que na prática se adopte um ponto de corte (cutoff point) para decidir do valor de n, e Wasserman e Faust (1994) sugerem que esse valor seja o da máxima distância geodésica conectando dois pares de actores num subgrupo coeso. Na esteira de Luce, n=2 é muitas vezes o ponto de corte adoptado, já que as 2-cliques são subgrafos em que há acessibilidade de todos os membros entre si através de pelo menos um nó sem que os nós sejam necessariamente adjacentes uns aos outros. Do ponto de vista metodológico, a análise de cliques é muitas vezes perturbada pelos próprios procedimentos do investigador, quando este limita arbitrariamente o número de escolhas ou rejeições (se for esse o gerador sociométrico em questão, claro) dos actores sociais.
Se G(m,p)=X corresponder a um dígrafo, xij< I significa que o arco <ni, nj> pertence a L. O produto xikxjk=1 se xik e Xjk=1, o que acontece se ambos os arcos <n1, nj> e <nj, ni> pertencerem a 1. isto reúne as condições para a existência do caminho ni,→ nk→ nj.
Assim, 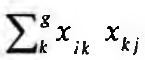 dá-nos o número de caminhos de comprimento 2 de n; para nj, para todos os nk. Como vimos acima, as entradas de
dá-nos o número de caminhos de comprimento 2 de n; para nj, para todos os nk. Como vimos acima, as entradas de 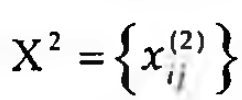 dão-nos as entradas de comprimento 2 para nj e, conforme os teoremas de Luce (1950), a matriz Xn o total de caminhos de comprimento n de nj para nj. O que nos conduz aos cálculos dos índices de centralidade e prestígio dos actores da rede social. Mais uma vez, o conceito de prestígio usado em ARS não tem necessariamente correspondência com conceptualizações sociológicas ou sociopsicológicas de prestígio, muitas vezes utilizadas e que recorrem a indicadores sociais e comportamentais estranhos ao conceito de rede social (sinais exteriores de riqueza podem ser e são muitas vezes utilizados nesse sentido, por exemplo). Dentro do quadro metodológico e conceptual da ARS, este conceito está estritamente delimitado pelo jogo de trocas e conexões entre actores sociais no interior da rede social em análise. Liga-se assim ao acima explicitado conceito de I-grau de um nó de um dígrafo, mas assume contornos mais complexos. De alguma forma, o prestígio na rede social liga-se ao posicionamento de um actor no sistema, e à sua proeminência grupai. Tome-se o exemplo da comunidade científica: é certamente factor de prestígio o número de citações de um autor por parte dos seus pares da rede social científica, uma medida do prestígio corresponderia ao grau de centralidade desse actor social medido não só pelas citações directas de que seria alvo, mas também pela própria centralidade e prestígio de quem o citaria, medidas por seu turno segundo os mesmo critérios, assumindo que não teriam o mesmo peso as citações produzidas por n estudantes ou por n cientistas laureados com prémios Nobel. Foi com base neste modo de ver as coisas que foi construído o índice de Hubbel (1965), incluído no package SDAS de Lan-geheine (cf. Soczka, 1996, para uma aplicação empírica). Ora, como Faucheux e Moscovici (1960) já o tinham sublinhado, a centralidade de um actor numa rede social vai a par com a excentricidade dos restantes, tal como para uma gama limitada de eleitores os votos depositados num dado partido representam necessariamente o custo para os restantes partidos concorrentes. No que respeita a uma rede social, o índice de centralidade é uma medida de variabilidade (dispersão/concentração) das emissões dos actores sociais. A centralidade CD de um actor nj numa rede social é-nos dada pela equação:
dão-nos as entradas de comprimento 2 para nj e, conforme os teoremas de Luce (1950), a matriz Xn o total de caminhos de comprimento n de nj para nj. O que nos conduz aos cálculos dos índices de centralidade e prestígio dos actores da rede social. Mais uma vez, o conceito de prestígio usado em ARS não tem necessariamente correspondência com conceptualizações sociológicas ou sociopsicológicas de prestígio, muitas vezes utilizadas e que recorrem a indicadores sociais e comportamentais estranhos ao conceito de rede social (sinais exteriores de riqueza podem ser e são muitas vezes utilizados nesse sentido, por exemplo). Dentro do quadro metodológico e conceptual da ARS, este conceito está estritamente delimitado pelo jogo de trocas e conexões entre actores sociais no interior da rede social em análise. Liga-se assim ao acima explicitado conceito de I-grau de um nó de um dígrafo, mas assume contornos mais complexos. De alguma forma, o prestígio na rede social liga-se ao posicionamento de um actor no sistema, e à sua proeminência grupai. Tome-se o exemplo da comunidade científica: é certamente factor de prestígio o número de citações de um autor por parte dos seus pares da rede social científica, uma medida do prestígio corresponderia ao grau de centralidade desse actor social medido não só pelas citações directas de que seria alvo, mas também pela própria centralidade e prestígio de quem o citaria, medidas por seu turno segundo os mesmo critérios, assumindo que não teriam o mesmo peso as citações produzidas por n estudantes ou por n cientistas laureados com prémios Nobel. Foi com base neste modo de ver as coisas que foi construído o índice de Hubbel (1965), incluído no package SDAS de Lan-geheine (cf. Soczka, 1996, para uma aplicação empírica). Ora, como Faucheux e Moscovici (1960) já o tinham sublinhado, a centralidade de um actor numa rede social vai a par com a excentricidade dos restantes, tal como para uma gama limitada de eleitores os votos depositados num dado partido representam necessariamente o custo para os restantes partidos concorrentes. No que respeita a uma rede social, o índice de centralidade é uma medida de variabilidade (dispersão/concentração) das emissões dos actores sociais. A centralidade CD de um actor nj numa rede social é-nos dada pela equação:
Correspondendo
à sua normalização, de forma a tornar o índice independente da dimensão g da rede ou sub-rede social em análise. Para um dígrafo, a proposta de Freeman (1979), no que respeita ao grau de centralidade grupai, recorrendo ao índice acima, é:
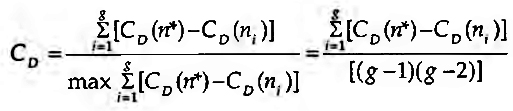
em que CD(ni) é o grau de centralidade do actor ni e CD(n*) representa o maior valor observado. Este valor é máximo num grafo em estrela, onde todos os nós convergem para um único nó a eles simétrico. O prestígio, estritamente associado a CD(ni) pode ser avaliado directamente pelo I-grau do actor social, ou seja: PD(ni)=dI(ni)=X+i. Se se quiser normalizar para tomar a medida independentemente da dimensão grupai, PD(ni)=(ni)=(x+i/(g-1)). Ora, como se referiu acima, o prestígio de um actor social não depende apenas dos totais marginais de recepções, mas também de toda a k-cadeia de emissores e do estatuto de cada um deles. Acontece que o prestígio e estatuto destes é também função do prestígio e estatuto de nj, o que nos coloca perante uma regressão infinita. De acordo com a proposta de Seeley (1949), que serviu de base à construção do índice de Hubbel acima referido, pode-se definir o prestígio de estatuto (isto é, o prestígio pesado pelos estatutos sociais dos emissores) PR(ni), tomando a coluna da socio-matriz contendo as entradas das recepções, e proceder ao produto dessas entradas pelos estatutos dos emissores, obtendo-se a combinação linear
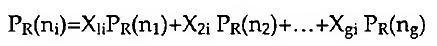
Chega-se assim a um sistema de g equações a g incógnitas, dado que a resolução de qualquer uma delas depende da resolução das restantes.
Se tomarmos a sociomatriz X e procedermos ao seu produto por um vector PR(ni), PR(n2),..., PR(ng)), contendo os índices de estatuto dos actores sociais, temos que p=X'p; ou seja, por rearranjo (X'-I)p=0, sendo I a matriz de identidade de dimensão igual ao total de actores sociais. Para quem esteja familiarizado com procedimentos de análise factorial ou de análise em componentes principais, esta equação será reconhecível. Com efeito, é a adequação usada para encontrar o sistema de valores próprios de uma matriz, em que p é um vector próprio da transposta da sociomatriz, correspondente ao valor próprio de 1. Wasserman e Faust (1994) sublinham que uma das soluções consiste em forçar X' a assumir esse valor próprio, dado que (tal como o frisara Katz, 1953), se tal se não fizer o sistema permanece irresolúvel.
A solução de Katz consiste na normalização da sociomatriz, de forma a obterem-se vectores-coluna de soma unitária. Wasserman e Faust (1994) defendem igualmente esta medida em ordem à resolução do sistema: "Encontra-se assim o vector próprio associado ao maior valor próprio de X' normalizada, unitário, e o vector próprio associado a este primeiro valor próprio será o vector de índices estatutários p". Para uma discussão matemática pormenorizada da ARS com denominação em vectores próprios (cf. Richards e Seary, 1997), com a particularidade interessante de estes autores integrarem a discussão no quadro de aplicações de análise multivariada bastante usadas em ciências sociais, como a análise de correspondências e a análise de covariância iterativa.4 O que nos remete para o problema da análise de estrutura das redes sociais.
Referimo-nos acima aos grafos valorizados e demos como exemplo típico da sua utilização os modelos de equilíbrio estrutural de Heider.
Partindo da definição de dígrafo de Cartwright e Harary (1956), ou seja, "um grafo é um dígrafo quando consiste num conjunto finito de pontos em que existe um dado subconjunto do possível conjunto de pares ordenados de pontos distintos"5 ligados entre si de forma assimétrica, é fácil de compreender que um grafo valorizado, ou S-grafo, é um caso particular de dígrafo. Heider, que no início dos anos 40 dedicara especial atenção à questão da percepção da causalidade, introduz num artigo de 1946 o princípio do equilíbrio cognitivo, que propõe como estruturante da percepção das relações sociais entre indivíduos. Seja uma díade composta por p e o entre os quais é estabelecida uma relação que pode assumir um de dois estados: positivo (L+) ou negativo (L-). A hipótese de Heider (1946) é a de que: a) existe um estado de equilíbrio se uma entidade possuí o mesmo carácter dinâmico em todos os sentidos, ou seja, pL(+)o ou pL(-)o para qualquer L; b) existe um estado de equilíbrio se todas as partes da unidade têm o mesmo carácter dinâmico (todas positivas ou todas negativas) e se entidades com diferentes traços dinâmicos se encontrarem segregadas uma da outra; c) se não existir um estado de equilíbrio, desenvolver-se-ão forças no sentido de o estabelecer; ou mudarão ou traços dinâmicos ou mudarão as unidades de relação mediante comportamentos ou reestruturações cognitivas.
Tal significa que, numa díade, existe equilíbrio se as relações entre os dois elementos da díade forem ou só positivas ou só negativas (pL(+)o e oL(+)p ou então pL(-)o e oL(-)p). Caso contrário, existe um estado de tensão (não-equilíbrio) entre p e o, e verificar-se-á um movimento de reequlibração da relação.
Similarmente, no caso de um tripleto, existe equilíbrio quando o produto das valências dos arcos ou linhas <o, p>, <o, k>, <j, k> é positivo. O que nos remete para o conceito de ciclo de um grafo: ciclo é um caminho fechado em que todos os nós excepto o de origem e o terminal são distintos uns dos outros. Num tripleto existem oito soluções combinatórias possíveis de ciclos de dimensão 3 entre o, p, k, sendo que quatro apresentam um sinal positivo no produto das valências das linhas incidentes, isto é, reúnem as condições de equilíbrio de Heider:
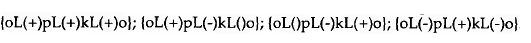
Cartwright e Harary (1956) e Harary, Norman e Cartwright (1965) aplicaram-se a generalizar matematicamente o modelo de equilíbrio estrutural de Heider para qualquer S-grafo completo. Cartwright e Harary (1956) demonstraram então que:
a) uma estrutura está em equilíbrio se todos os seus ciclos são positivos;
b) uma estrutura está em equilíbrio se todos os nós do S-grafo que a representa todas as semivias que os unem têm o mesmo sinal, isto é, se os produtos das suas linhas têm os mesmos sinais;
c) uma estrutura está em equilíbrio se o conjunto de todos os nós do S-grafo se pode dividir em dois conjuntos (um dos quais pode ser vazio) tais que cada linha positiva liga dois nós do mesmo subconjunto e cada linha negativa liga dois nós de subconjuntos diferentes.
Esta última conclusão conduziu aos teoremas da conglomeração de Davis (1967), que veremos adiante (entre muitas outras, uma verificação empírica da conglomeração está contida em Soczka, 1984). Ora, se é trivial avaliar o equilíbrio estrutural de Heider em S-grafos ou dígrafos de pequena dimensão, já não o é se o que estiver em questão forem sociomatrizes de ordem elevada. Para um S-grafo, se este estiver em equilíbrio, a diagonal de Xn (n representando a n-ésima potência da sociomatriz de ordem g) deve apresentar valores positivos para todas as potências n=1, 2,..., g.
A verificação empírica de um S-grafo se pode subdividir em conglomerados (clusters) tais que as relações entre ambos sejam negativas e nos seus respectivos semiciclos sejam positivas, levou à seguinte definição da conglomeridade de uma rede social (Davis, 1967):
Um S-grafo é conglomerável ou possui um conglomerado se for possível dividir os seus nós num número finito de subconjuntos tais que cada linha positiva liga dois nós do mesmo subconjunto e cada linha negativa liga dois nós de subconjuntos diferentes, designando-se cada um desses subconjuntos por conglomerado.
Como se vê, trata-se de uma generalização para k-clusters da conclusão c) de Cartwright e Harary acima apresentada. A conglomeração proposta por Davis alarga o modelo de Heider, dado que admite num mesmo conglomerado relações não positivas, ou seja: uma estrutura pode não estar em equilíbrio e ser ainda assim subdivisível em conglomerados coerentes com a definição acima dada.
Na análise estrutural de uma sociomatriz, os elementos relacionais mínimos são obviamente as relações diádicas, ou seja, as relações possíveis entre cada dois elementos diferentes da sociomatriz. Como sempre, em ARS, impõe-se a condição da relação intransitiva de cada elemento consigo próprio, ou seja, Xii=0. Sendo assim, como se disse acima, três estados são possíveis entre cada par <i, j>: relação nula (N), assimetria (A), (i → j ou j → i mas não ambos), e reciprocidade relacional (M). Estes três estados geram assim um conjunto de quatro relações diádicas D possíveis: Dij=(0,0) ou relação nula, Dij=(1,0) e Dij(0,l) ou as duas possibilidades de assimetria, e Dij=(l,l) quando se verifica reciprocidade. Ao varrimento da sociomatriz em ordem à contagem das ocorrências reais de cada uma destas quatro possibilidades de isomorfismos chama-se censo diádico. De tal forma que
Equação 17
Longe de constituir um mero exercício de estilo, o censo diádico é a base para a medida das discrepâncias entre os valores realmente observados numa dada sociomatriz e os valores expectáveis se as escolhas fossem verdadeiramente aleatórias, possibilitando assim a passagem ao raciocínio estatístico em sociometria. Esta preocupação coincide com os próprios primórdios da análise sociométrica, a começar pelo seu próprio fundador, Moreno (cf. Soczka, 1984; entre os trabalhos pioneiros nesta matéria contam-se os de Moreno ejennings, 1938; Urie Bronfenbrenner, 1945; e Criswell, 1946). Em condições de levantamento sociométrico com um número d de escolhas fixas, a probabilidade de uma relação simétrica entre os actores sociais i e j numa sociomatriz gxg ser-nos-ia dada pela equação 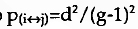 , se as escolhas fossem aleatórias e com distribuição uniforme. Assim,
, se as escolhas fossem aleatórias e com distribuição uniforme. Assim,
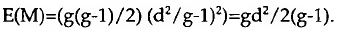
Ora, muitas vezes a ARS baseia-se num único gerador sociométrico, ou critério de selecção, por exemplo, quem numa empresa escolhe quem para ir almoçar, ou num grupo de adolescentes (a idade dos telefonemas contínuos de uns para os outros, como todos os pais bem sabem quando recebem a conta da Telecom) quem telefona a quem. Mas há condições em que aos actores sociais se apresentam múltiplos geradores sociométricos, ou seja, múltiplos critérios de selecção, de tal maneira que possa acontecer, por exemplo, simetria entre i e j para o critério ci e assimetria para o critério C2. Nesse caso, o problema complexifica-se um pouco. Em 1946, Joan Criswell apresentou uma forma simples de avaliar a coerência intercriterial. O censo diádico é assim efectuado Cn vezes. Se cada actor social fizer d selecções em cada critério, faz no total C2d selecções para o conjunto de (g-1) actores. E
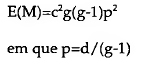
Caso d não seja constante entre dois geradores sociométricos, o cálculo proposto por Criswell (1946) é inviável. Ou seja, é limitado aos casos de ARS com escolhas fixas. No caso de um sociograma "aberto", em que não há limite para o número de arcos entre dois nós de um dígrafo a não ser o imposto pelo próprio número total de nós, há que ter em conta não só 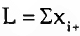 , ou seja, o total de selecções, mas também o número de selecções efectuadas por cada actor social. Seja
, ou seja, o total de selecções, mas também o número de selecções efectuadas por cada actor social. Seja 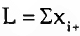 . A probabilidade de M(i, j) será
. A probabilidade de M(i, j) será 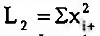 se as relações forem aleatórias e com distribuição uniforme. Então,
se as relações forem aleatórias e com distribuição uniforme. Então,
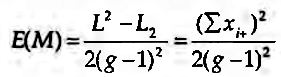
Com o pressuposto de que a distribuição das escolhas (leia-se selecções, interacções ou qualquer outra medida das relações diádicas) é aleatória num espaço amostrai S={0,1}, estamos perante uma distribuição de Bemouill de acontecimentos independentes. No caso dos dígrafos, a distribuição uniforme das escolhas põe a hipótese de que todos os actores sociais escolhem 50% dos restantes actores, isto é, {Pij}=0,5.
Assumindo que, dado o gerador sociométrico c, é equiprovável a emissão do comportamento c do elemento i de um conjunto de g actores para os restantes (g-1) actores, cada um deles será alvo do comportamento gerado a partir de c com uma probabilidade p=1/(g-1), e haverá a probabilidade q=1-p de o não ser.
A significância estatística das discrepâncias entre cq e p(cq) foi testada por Moreno (1934) e por Moreno e Jennings (1938) mediante o teste x2/ enquanto Bonfen-brenner (1945) adoptou como critério os limites de confiança da média dados por 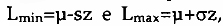 , onde z corresponde ao valor da normal reduzida:
, onde z corresponde ao valor da normal reduzida: 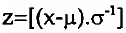 . Na prática estas vias são equivalentes (Soczka, 1984), dado que
. Na prática estas vias são equivalentes (Soczka, 1984), dado que
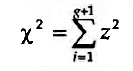
Com efeito, numa série g+1 conjuntos independentes Ai... Ag+i, em que pi= p(Aj), i=1...g, em Ni repetições independentes de tal modo que
Equação 27
Disse-se acima que a análise estrutural de uma rede social tem como constituinte mínima a análise diádica. No entanto, muitos dos desenvolvimentos realizados em ARS, incluindo todos os que giram à volta do modelo de equilíbrio de Heider e todos os que se realizam em torno da questão da participação em cliques e subgrupos, pressupõem o passo seguinte: a análise das relações triádicas. Em sociometria, a avaliação das relações diádicas apresenta em si mesma interesse, sobretudo quando ao investigador interessa estudar os atributos de cada actor social nas suas relações com cada um dos restantes actores. E esse é muitas vezes o caso em psicologia. Mas para se abordar a estrutura das redes sociais em si mesmas consideradas, é possível passar a um nível de análise n-diádico (para n>2), e o caso mais básico será então o nível das relações triádicas. À contagem classificativa das 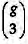 tríades encontradas numa dada sociomatriz de acordo com os 16 tipos de Holland e Leinhardt (1970), chamaram Davis e Leinhardt (1972) o censo triádico.
tríades encontradas numa dada sociomatriz de acordo com os 16 tipos de Holland e Leinhardt (1970), chamaram Davis e Leinhardt (1972) o censo triádico.
Holland e Leinhardt (1971) reviram o modelo de equilíbrio estrutural de Heider e demonstraram ser ele um caso particular de um modelo mais geral, baseado no conceito de transitividade, apresentando a seguinte definição de transitividade: "Uma tríade composta pelos actores i, j e k é transitiva se sempre que i → j e j → k, i → k". Do que decorre que "Um dígrafo é transitivo se cada tríade que contém for transitiva".
Num dígrafo transitivo ou T-grafo, portanto, não existem tríades assimétricas e um T-grafo é subdivisível em conglomerados. Numa sociomatriz, ou no dígrafo que a representa, para se verificar se uma relação é transitiva, é necessário examinar todas as tríades ordenadas de indivíduos distintos (censo triádico). Como decorre da definição de transitividade, se i → j e j → k, i → k. Caso i → j e j → k; mas i-/-> k, ocorre intransitividade na tríade. Como sabemos em cada par da tríade é possível encontrar uma relação mútua (M) (reciprocidade), assimétrica (A) ou nula (N). Como se referiu acima, Holland e Leinhardt (1970) estabeleceram então códigos descritivos dos 16 tipos possíveis (201 significa que se trata de uma tríade com duas reciprocidades, sem assimetrias e com uma relação nula, 300 uma dique conexa, etc.), diferenciando os tipos não isomórficos por letras (por exemplo: três das tríades apresentam zero reciprocidades, duas relações assimétricas e uma relação nula, mas não são estruturalmente isomórficas; são portanto distinguidas pelos códigos 021D, 021U e 021C).
Ora, para uma dada sociomatriz é possível estabelecer um índice de transitividade C, pela comparação do número de intransitividades encontradas com as que se poderiam estatisticamente com as que se poderia estatisticamente encontrar numa sociomatriz aleatória. Seja T o número de tríades intransitivas num dígrafo e Pt e ot as respectivas média e desvio-padrão, sob a hipótese nula de que a sociomatriz é aleatória. Define-se o índice de transitividade
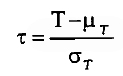
que por se apresentar normalizado pode ser referido a uma tabela de distribuição normal para o cálculo dos seus limiares de significância (cf. Holland e Leinhardt, 1970, para a demonstração e comparação com o índice de Davis e Leinhardt (1970) 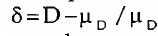 , onde D é o número de tríades não-admissíveis e µD o seu valor esperado em condições de aleatoridade).
, onde D é o número de tríades não-admissíveis e µD o seu valor esperado em condições de aleatoridade).
Como se afirmou acima, a ideia de comparar os resultados sociométricos empíricos com modelos sociométricos aleatórios em ordem a avaliar modelos de hipótese nula remonta aos tempos "heróicos" dos pioneiros, e o próprio Moreno (1953) gerou sociomatrizes aleatórias com esse objectivo. E constantemente se encontrou que a distribuição de estatutos e popularidade grupai (ou de escolhas recebidas) estava longe de ser aleatória e que o número de escolhas recíprocas M era também superior ao que se poderia esperar em condições de acaso. Ora o que se verifica é que existiu desde o início um erro de raciocínio nesta abordagem do problema, e que consistiu na ignorância da multicolinaridade dos dados: a distribuição aleatória da popularidade (X+j) não pode ser a mesma de M, dado que o aumento do I-grau de um actor social incrementa logicamente a probabilidade de para esse actor se verificarem mais reciprocidades, enquanto que actores sociais de menor I-grau têm menores probabilidades de relações recíprocas (ou nenhumas, se forem isolados de I-grau nulo). O que significa que as probabilidades são condicionais a X+g e a Xg+ numa sociomatriz de ordem g, tal como já havia sido sublinhado por Katz e colaboradores (1958). E é assim que, para o cálculo da distribuição de T, Holland e Leinhardt (1970) têm em conta quer as escolhas recebidas (X+i), quer as escolhas emitidas (Xi+), quer o valor de M.
Tormando as 16 classes isomórficas, o censo triádico correspondente ao vector 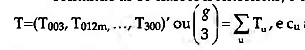 ao número de arcos em cada um dos tipos de tríade (c1=0, ...c16=6). Assim,
ao número de arcos em cada um dos tipos de tríade (c1=0, ...c16=6). Assim,
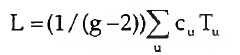
corresponde ao número total de arcos de um dígrafo e X= L/g ao I-grau médio=O-grau médio do dígrafo. Holland e Leinhardt (1975) calcularam as estatísticas das variâncias para as emissões e recepções do censo triádico.
Um problema que desde sempre preocupou os sociometristas foi o da variação no tempo das configurações das sociomatrizes, mas até há pouco tempo não se dispunha de modelos estatísticos adequados para se proceder a análises dessas variações. Apropria hipótese de equilíbrio de Heider, que contém em si mesma uma previsão de mudança do estado de um sistema triádico, é ainda insuficiente como modelo de previsão pois, como o sublinhou Doreian (1970), "a hipótese do equilíbrio não faz mais do que prever que ocorrerá uma transformação. No que toca ao modo como se fará essa transformação, nada afirma". Sobretudo, não nos fornece um modelo de transformação das configurações sociométricas no tempo, o que seria possível através de outros modelos que fossem baseados na probabilidade de ocorrência de um dado estado do sistema em função da ocorrência de estados anteriores desse mesmo sistema, como sejam os modelos markovianos ou os modelos log-lineares.
O problema da análise da transformação no tempo de uma rede social pressupõe a possibilidade técnica de comparação entre duas sociomatrizes, tanto no que respeita à comparação de dois ou mais estados de uma mesma rede, como à comparação entre várias redes simultâneas. Os modelos log-lineares centraram-se, num primeiro momento, na análise de uma mesma rede social (sobretudo a partir da distribuição pi de Holland e Leinhardt, 1977; 1981) e, mais recentemente, surgiram trabalhos especificamente orientados para as análises multi-redes (cf. por exemplo, Banks e Carley, 1994; Sanil, Banks e Carley, 1995). Atendamos então, primeiro, ao problema da análise de uma única relação entre dois actores <ni, nj> de uma rede social com g actores, logo 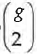 díades, ou seja 2
díades, ou seja 2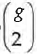 variáveis diádicas aleatórias. Num dígrafo, a relação entre i e
variáveis diádicas aleatórias. Num dígrafo, a relação entre i e 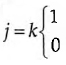 não é necessáriamente idêntica à relação entre i e
não é necessáriamente idêntica à relação entre i e 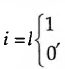 e assim para cada par de actors é possível construir uma tabela de contingência 2x2. Numa sociomatriz gxg, obtém-se então uma tabela de contingência gxgx2x2.
e assim para cada par de actors é possível construir uma tabela de contingência 2x2. Numa sociomatriz gxg, obtém-se então uma tabela de contingência gxgx2x2.
Num dígrafo valorizado, em que as relações entre i e j podem assumir vários positivos C, teremos gxgxCxC=Yijk onde Yijk=1 se a díade Dij assumir os valores Xij=k, Xji=1 e Yijk=0 em caso contrário. Ou seja, uma tabela de contingência quadri-dimensional (4D), em que cada célula (i, j) é uma submatriz CxC. Holland e Leinhardt (1981) desenvolveram os cálculos para uma distribuição exponencial, designada pi, e construíram para a análise de sociomatrizes binárias uni e multivariadas um modelo log-linear análogo ao da ANOVA; a logaritmização é feita para que possa operar a linearização da multiplicacidade inicial.
Na notação de Goodman (1972; cf. Knoke e Burke, 1980), as frequências esperadas numa dada célula i de uma tabela de contingências a duas variáveis KxC são-nos dadas por 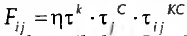 , em que x representa os "efeitos" das variáveis nas frequências das células. Sendo q a média geométrica dos efectivos de cada célula;
, em que x representa os "efeitos" das variáveis nas frequências das células. Sendo q a média geométrica dos efectivos de cada célula; 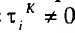 , para cada nível i de K, se se verificar distribuição desigual da variável K nas categorias da variável
, para cada nível i de K, se se verificar distribuição desigual da variável K nas categorias da variável 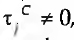 , para cada nível j de C, se se verificar distribuição desigual da variável C nas categorias da variável K; e
, para cada nível j de C, se se verificar distribuição desigual da variável C nas categorias da variável K; e 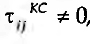 , para cada uma das ij células, se C e K não forem independentes. Assim,
, para cada uma das ij células, se C e K não forem independentes. Assim,
Equação 41
O modelo pi de Holland e Leinhardt (1981) parte dos quatro estados possíveis de uma díade (relação nula, Xij=Xji=0, ou Yij11=1; recíproca, Xij=X
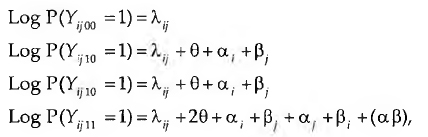
com os condicionalismos
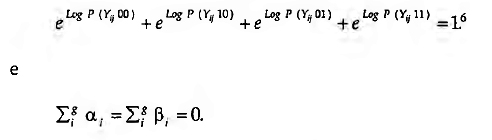
O parâmetro θ é correspondente no modelo log-linear geral a uma média geométrica das emissões e recepções globais, e ao logaritmo do que numa equação de regressão se designa por termo de intercepção. No caso de Yijoo=1, o valor de θ é obviamente zero. Os parâmetros {a.} expressam a expansividade (O-grau) do actor e os parâmetros (ß, ) o seu I-grau (correspondente muitas vezes em sociometria à sua popularidade directa, como se viu acima). Os parâmetros (α ß)7 correspondem a medidas das reciprocidades diádicas e correspondem à probabilidade condicional de i → j se j → i. Se atendermos ao modelo log-linear anteriormente apresentado, os parâmetros A. da distribuição pi são equivalentemente correspondentes aos efeitos das interacções diádicas por forma a que os condicionalismos acima sejam sustentáveis. Seja n a probabilidade de ocorrência da observação (k, l) na díade (i, j), ou seja, P (Yijkl) com 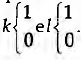 . Então, o efeito de reciprocidade da díade (i, j) será
. Então, o efeito de reciprocidade da díade (i, j) será
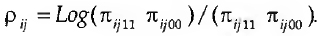
Para que este valor não se fixe entre +∞, e -∞ Holland e Leinhardt (1981) forçaram Pij=p para todo i≠j. Se se assumir que todas as díades são estatisticamente independentes, a função de verosimilhança logarítmica para o modelo pi será para y
Equação 46
Como é visivel, o modelo p1 usa fundamentalmente os totais marginais de y. Como yijkl=yijkl' as contagens são duplicadas, logo

Ajustar a distribuição p1 a uma sociomatriz observada corresponde assim a constituir uma sociomatriz de valores esperados com I-graus, O-graus, M e x++ iguais aos da sociomatriz observada para se poder proceder a uma comparação entre ambas as distribuições. A estimativa dos parâmetros de pi é dada em Fienberg e Wasserman (1981). O modelo não trabalha directamente com os parâmetros p, θ, α1 eβj recorrendo, como se viu, a uma abordagem indirecta a partir dos totais marginais e do total de totais marginais. Ora, sendo , decorre que
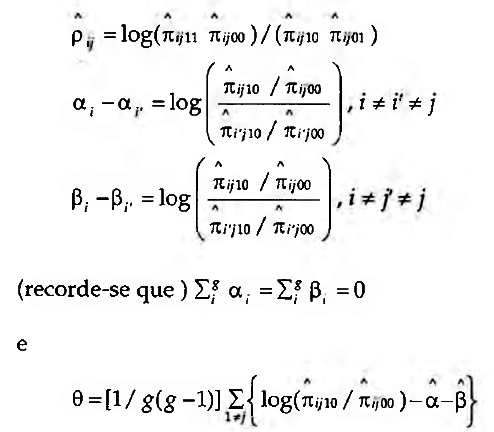
O modelo p1 pressupõe independência diádica, e assim obsta à utilização de teorias que envolvam cliques e transitividades (Banks e Carley, 1996), e em geral do modelo de distribuição MAN para o censo triádico, a que acima se fez referência. Para matrizes binárias do censo diádico, Holland e Leinhardt (1977) e Wasserman (1980) desenvolveram modelos em que os comportamentos diádicos são independentes no tempo to mas markovianamente dependentes de comportamentos anteriores no tempo to+xO modelo de Holland-Leinhardt permitiu também avanços no que respeita às técnicas de partição de uma sociomatriz em blocos estruturalmente equivalentes, ou blockrnodeling, ou seja: grupos de actores sociais que constituem subconjuntos de tal forma coerentes que esses actores são equivalentes e são intersubstituíveis no que respeita às suas posições e papéis na sociomatriz.8 O conceito de equivalência estrutural foi proposto por Lorrain e White (1971) como uma propriedade matemática dos actores, de tal forma que dois actores são equivalentes se tiverem exactamente as mesmas ligações com todos os restantes actores numa rede social para uma dada relação social (ou gerador sociométrico). Para um universo R (Xi, X2,... Xr) de relações sociais, 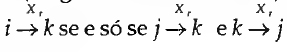 para todos os actores k=1,2 ...g (k≠i, j), e relações r=1, 2...R.
para todos os actores k=1,2 ...g (k≠i, j), e relações r=1, 2...R.
Ou seja, i e j são equivalentes se para as ligações de j e i com todos os restantes actores são iguais, para todos os geradores sociométricos considerados, isto é, têm exactamente as mesmas entradas em todas as sociomatrizes. Verifica-se assim um isomorfismo entre todos os actores estruturalmente equivalentes, quer se trate de uma sociomatriz binária, quer se trate de uma sociomatriz valorizada, em que as ligações entre actores sejam definidas por escalas ordinais, como acontece sempre que o gerador sociométrico é medido por uma escala de Likert onde se avalie não só a existência de ligação mas também o seu peso.
Podem portanto constituir-se subconjuntos de actores em função dessa equivalência estrutural, ou classes de actores com a mesma posição sociométrica na rede ou conjuntos de redes. Uma segunda matriz, dita de imagem, é deste modo construída, reflectindo já não as ligações entre actores singulares mas entre classes de actores com a mesma posição: um modelo de blocos posicionais, ou blockmodel.9
Ora, assim definida, a equivalência estrutural é um modelo matemático ideal, com restrições demasiado exigentes para ter uma mais do que frágil correspondência com as realidades psicológicas e sociológicas empíricas, as quais obviamente são realidades em mudança, incompatíveis com modelos matemáticos rígidos. O problema que se põe é, portanto, o de avaliar os actores em termos de uma relativa equivalência estrutural. Dado que o que está em questão é sempre a comparação dos vectores-linha de i e de j na sociomatriz, o problema não é diferente do da comparação de perfis com que tantas vezes a psicometria se debate (por exemplo, a comparação entre dois perfis psicológicos obtidos numa bateria de testes ou num teste plurifactorial como o 16PF). Para efeitos de diagnóstico, dificilmente se poderá exigir que dois sujeitos apresentem exactamente o mesmo perfil, ponto por ponto, para se poder dizer que pertencem à mesma classe diagnóstica. O que se procura então é saber como determinar que, apesar de existirem diferenças, essas diferenças são insignificantes para se proceder à classificação na mesma classe de ambos os sujeitos, com um mínimo de erro ou com um erro estatisticamente conhecido e previsto.
Duas formas clássicas de comparação de perfis são frequentemente utilizadas: o caso particular de um espaço de Minkowski a R2, que são as distâncias euclidianas, e a correlação de produto-momento. No caso de uma sociomatriz, em que xik denota e relação entre i e k, e Xjk a relação entre j e k, a distância euclidiana entre dois actores sociais i e j é-nos dada por:
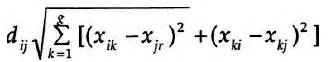
No caso de se tratar de múltiplas sociomatrizes, cada uma correspondendo a um particular gerador sociométrico, r (r=1, 2...R),
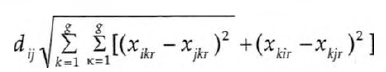
E a correlação de Pearson, para um gerador sociométrico:
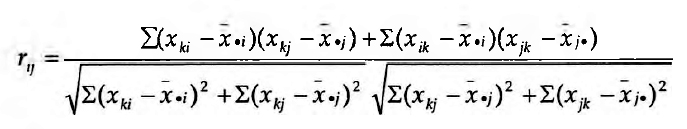
onde xi denota a média aritmética da linha i e x.i a média aritmética da coluna i com exclusão da diagonal.10
Paralelamente, para R geradores sociométricos,
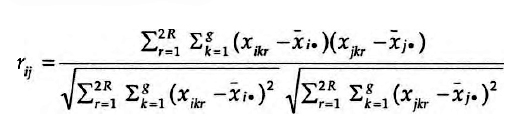
para k≠i, j.
Esta passagem para a relatividade da equivalência permitiu ultrapassar as limitações rígidas do conceito de equivalência estrutural e passar ao conceito de equivalência estocástica, onde os blockmodels são construídos com base nas probabilidades de relações entre eles para um dado gerador sociométrico, em função de uma distribuição de probabilidades p(x). Passos nesse sentido foram dados por Hol-land, Laskey e Leinhardt (1983), a partir dos trabalhos previamente desenvolvidos por Holland e Leinhardt (1981) sobre a distribuição log-linear pi acima referida.
Os blockmodels estruturais, como o notam Wasserman e Faust (1994), são um caso particular de equivalência estocástica, onde as relações entre actores de uma dada classe posicionai e actores de outra classe posicionai é binária, e portanto têm uma probabilidade 1 ou 0 de ocorrer. Na modelagem estocástica, essa probabilidade de ocorrência tem uma distribuição entre 0 e 1, o que a torna muito mais rica do ponto de vista informativo.
A construção de modelos de previsão para a mudança das relações pessoais num grupo é um sonho antigo da psicologia social, desde o referido modelo de Heider (1946; 1958) até às teorias da comparação social e da dissonância cognitiva (Festinger, 1954; 1957). Em todos estes exemplos, acreditou-se que seria possível construir modelos matemáticos das mudanças grupais a partir das mudanças das relações interpessoais. Sem sucesso, aliás, provavelmente porque, tal como antevira Kurt Lewin (1947), a dinâmica de mudança num grupo não é legível a partir do somatório de mudanças individuais, e como se sabe Lewin preferiu recorrer à teoria de campo para dar conta dessa dinâmica. O modelo de Heider baseia-se numa perspectiva puramente cognitivista da dinâmica de mudança que, independentemente dos formalismos matemáticos de que foi alvo, roça a ingenuidade. Ao postular que o equilíbrio (cognitivo) só é possível quando o produto das valências dos arcos intermodais do tripleto é positivo, o modelo de Heider postula um universo de aparelhos psicológicos de funcionamento estritamente binário, ou seja, repousando em processos psicológicos de clivagem.
É claro que esses processos de clivagem são reais (e por definição só não serão óbvios para o próprio sujeito que os utiliza, que poderá escapar a essa evidência por identificação projectiva) mas, felizmente para o mundo das relações interpessoais, nem tudo é clivagem e identificação projectiva. A experiência pessoal de todos os seres humanos revela que as percepções e as relações interpessoais são de uma extraordinária complexidade multidimensional. Se {oL(+)pL(-)kL(+)oi} está desequilibrado segundo o modelo de Heider, e (oL(+)pL(+)kL(+)o2) está em equilíbrio segundo o mesmo modelo, é bem possível que ambas as condições coexistam, sem que haja nenhuma necessidade de dinâmicas de reequilíbrio. Ou seja, para que as dinâmicas de reequilíbrio fossem imperativamente necessárias, como postula o modelo de Heider, seria também imperativo que duas pessoas não pudessem coexistir numa relação equilibrada afectiva e cognitivamente sem que tivessem exactamente as mesmas atitudes, crenças e gostos em relação a um terceiro objecto, logo com plena equivalência estrutural, o que seria absurdo.11 E, sobretudo que, dado um conjunto de on objectos, só existisse equilíbrio se, de forma global, nas relações de p e k com esses objectos o produto das valências fosse positivo. O que, pelo menos, seria limitativo, e nem sequer contemplaria a eterna ambivalência presente nas relações humanas, sem por isso as desequilibrar necessariamente.
O modelo de equilíbrio de Heider é, de facto, uma das primeiras formulações de uma previsão das dinâmicas de relações interpessoais. Para uma sociomatriz X com ligações não dirigidas, isto é, para grafos mas não dígrafos, o modelo de Heider prevê que em dois momentos do tempo X(tq) e X(tq+i)se verificam mudanças tais que ocorre a adição de ligações entre nós que possuem uma ligação com um nó comum, de forma a que a tríade fique completamente conectada. O modelo heideriano pressupõe assim estabilidade estocástica de uma tríade <i, j, k> de tal forma que se Xij(tq)=0:
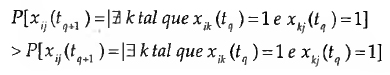
No tempo tq/ há numa tríade r/2 possibilidades de mudança das ligações entre nós num grafo. Seja n o potencial acréscimo do número de ligações entre nós que produziram uma tríade conexa; seja T2 o potencial acréscimo do número de ligações entre nós que não produziriam uma tríade completamente conexa; e seja Yi o número de acréscimos observados de tq para tq+i que completariam uma tríade, bem como Y2 o número de acréscimos observados de tq para tq+i que não completariam uma tríade. O teste binomial para proporções pode então ser usado para testar se Yi /ri é significativamente diferente de Y2/r2 (Banks e Carley, 1996). O modelo de Heider não contempla, no entanto, o caso da anulação de ligações entre os actores sociais.
Por outro lado, como o fizeram notar Chase (1974,1980), no plano da etologia social, e Carley (1990), na peugada da melhor tradição do estudo dos grupos humanos (Lewin, 1947; Homans, 1950; Bales, 1950), a dinâmica de um grupo não pode ser lida exclusivamente a partir das relações diádicas, e tem de recorrer à totalidade das influências das interacções de todos os membros do grupo (cf. Soczka, 1974; 1984). Acresce que o tema central de Kurt Lewin, a mudança é, curiosamente um dos conceitos mais ausentes da maioria das investigações em psicologia social, que na procura positivista de grandes leis estáveis para o comportamento e a cognição humana, esquece-se espantosamente da temporalidade de todos os fenómenos humanos (Soczka, 1997), e olha para os seus objectos como fixos no tempo, pendurados numa eternidade mítica e portanto desumana. A psicologia social persistiu na negação da temporalidade, e denega a mudança num mundo em mudança, 50 anos depois de Kurt Lewin.
E claro que toda a construção de um modelo implica uma redução, e essa redução está contida no próprio conceito de modelo. No caso de um modelo matemático, seria impossível nele conter a imensa complexidade dos processos psicológicos e das relações humanas sem perdas, e o mais que se pode é tentar não eliminar no modelo componentes essenciais para a gama limitada de fenómenos que se pretenda prever.
Sem incorrer nas limitações do modelo de equilíbrio de Heider, Carley (1990) propõe, por exemplo, um modelo sociocognitivo para a estabilidade de um grupo, sem impor constrições ao conceito cognitivo, ou seja, não postulando a equivalência de cognitivo=consistente-para-o-sujeito, mas simplesmente cognitivo=conjunto de informação disponível para um dado sujeito, consciente ou não, incluindo afectos.
Seja I o conjunto de indivíduos num dado grupo, e K um conjunto de factos ou informações disponíveis para pelo menos um dos membros do grupo. Ora, em cada momento t do tempo, um indivíduo i está ou não a par de uma dada informação k, sendo k ∈ K, ou seja, 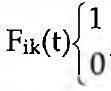 , conforme i conheça (1) ou não conheça (0) o facto k. Cada cultura ou subcultura possui um padrão próprio de distribuição de K em I, e estrutura-se socialmente, de tal forma que cada membro i do grupo tem uma maior ou menor probabilidade de interagir com um dado membro j do mesmo grupo. Seja Pij(t) a probabilidade de essa interacção ocorrer no momento t. Com algumas restrições necessárias, tais como todos os elementos k serem informativamente equivalentes e a troca de informações dissonantes entre i e j não produzir conflito mas acréscimo de informação (o que como postulado é exactamente o contrário do postulado proposto por Heider), Carley (1990) desenvolve a partir das definições acima um interessante modelo dinâmico que atende simultaneamente aos processos diádicos e aos processos grupais. Seja INTij(t) a efectiva interacção dos sujeitos i e j no momento t, e Uik(t) a comunicação por i a j do facto k (com uma escolha aleatória de qualquer k de entre o conjunto ki,..., kn de factos conhecidos por i) no momento t. O modelo de Carley assume que é irrelevante qual dos k é escolhido por i, ou seja, a informação é equivalente.
, conforme i conheça (1) ou não conheça (0) o facto k. Cada cultura ou subcultura possui um padrão próprio de distribuição de K em I, e estrutura-se socialmente, de tal forma que cada membro i do grupo tem uma maior ou menor probabilidade de interagir com um dado membro j do mesmo grupo. Seja Pij(t) a probabilidade de essa interacção ocorrer no momento t. Com algumas restrições necessárias, tais como todos os elementos k serem informativamente equivalentes e a troca de informações dissonantes entre i e j não produzir conflito mas acréscimo de informação (o que como postulado é exactamente o contrário do postulado proposto por Heider), Carley (1990) desenvolve a partir das definições acima um interessante modelo dinâmico que atende simultaneamente aos processos diádicos e aos processos grupais. Seja INTij(t) a efectiva interacção dos sujeitos i e j no momento t, e Uik(t) a comunicação por i a j do facto k (com uma escolha aleatória de qualquer k de entre o conjunto ki,..., kn de factos conhecidos por i) no momento t. O modelo de Carley assume que é irrelevante qual dos k é escolhido por i, ou seja, a informação é equivalente.
A efectiva comunicação de k a j por i em t, é:
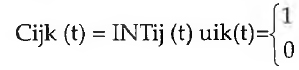 conforme i comunique (1) ou não (0) k a j.
conforme i comunique (1) ou não (0) k a j.
Assumindo a equivalência das informações ou factos a transmitir, Uik(t) assume a forma u(a, x, b) em que x é o x-ésimo facto do conjunto de factos conhecidos por I, traduzido por a e b no k-ésimo facto do conjunto de K factos. Seja 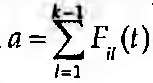 numero de factos conhecidos por i cujo índice é inferior a k, e
numero de factos conhecidos por i cujo índice é inferior a k, e 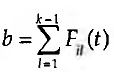 o conjunto de factos conhecidos por i de índice igual ou inferior a k. O modelo de Carley assume que a informação transmissível é equivalente, mas não amorfa a estrutura social dos emissores e receptores da informação. Assim, há que considerar a selectividade interpessoal, ou seja, qual dos indivíduos em I, i escolhe no momento t para interagir. Para tal, e dado que é assumida uma estrutura diferencial das comunicações, ou seja, uma estrutura social para o grupo, há que atender à probabilidade de o indivíduo i interagir com j, Pij(t), e também à disponibilidade de j nesse momento, Aj(t). A função Vij(Pij(t), Aj(t)) assume a forma v(a, y, b) em que a representa a probabilidade condicional de i interagir com qualquer indivíduo h entre 1 e j-1, e b a probabilidade condicional de isso acontecer com qualquer indivíduo h entre 1 e j. Ou seja:
o conjunto de factos conhecidos por i de índice igual ou inferior a k. O modelo de Carley assume que a informação transmissível é equivalente, mas não amorfa a estrutura social dos emissores e receptores da informação. Assim, há que considerar a selectividade interpessoal, ou seja, qual dos indivíduos em I, i escolhe no momento t para interagir. Para tal, e dado que é assumida uma estrutura diferencial das comunicações, ou seja, uma estrutura social para o grupo, há que atender à probabilidade de o indivíduo i interagir com j, Pij(t), e também à disponibilidade de j nesse momento, Aj(t). A função Vij(Pij(t), Aj(t)) assume a forma v(a, y, b) em que a representa a probabilidade condicional de i interagir com qualquer indivíduo h entre 1 e j-1, e b a probabilidade condicional de isso acontecer com qualquer indivíduo h entre 1 e j. Ou seja:
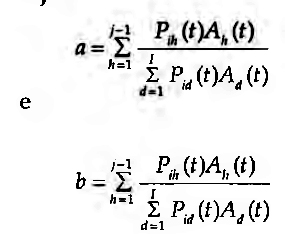
Ora, um dos factos comprovados em sociometria e na psicossociologia das relações interpessoais é a ocorrência de homofilia (Homans, 1950; Lazarsfeld e Merton, 1954; Maisonneuve, 1966; Soczka et al, 1985; Borges, 1994), ou seja: as redes sociais espontâneas são constituídas com maior probabilidade por indivíduos que partilham características semelhantes (sexo, idade, posição social, níveis académicos, atitudes e crenças, ideologias, ou até mesmo simples vizinhança, o efeito de propinquidade) do que por indivíduos dissonantes nessas características. O modelo de Carley incorpora a homofilia, postulando que quanto mais dois actores sociais são similares no que respeita à informação disponível para cada um, mais provável é que estabeleçam um interacção directa. Essa similaridade social, real ou percebida, incrementa a probabilidade de interacção Pij(t):
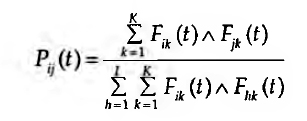
Ou seja, a probabilidade de interacção entre dois actores sociais é função da quantidade de informação partilhada entre ambos e da informação partilhada com todos os restantes elementos de I. Obviamente, tal depende ainda da disponibilidade do interlocutor no momento t, pelo que a interacção entre i e j é condicional, ou seja, INTij(t)=vij((Pij(t), Aj(t)).
Em ARS há que distinguir entre os modelos matemáticos que servem para comparar a estrutura de diversas redes (embora essas comparações possam efectivamente respeitar à mesma rede medida em momentos distintos do tempo; cf. Wasserman e Iacobucci, 1988) e os modelos que procuram dar conta da dinâmica das redes, ou seja, modelos psicológicos ou sociológicos do próprio processo de evolução das redes no tempo. Há que reconhecer que se deram bastante mais passos no primeiro sentido do que no segundo, embora ainda hoje não se disponha de modelos estatísticos adequados para a análise de séries temporais de redes sociais (Doreian, 1970,1990; Banks e Carley, 1996). O que significa que estamos perante um risco, como sempre acontece quando a formalização matemática toma a dianteira em relação à teorização em ciências sociais: o risco de construção de modelos formalmente correctos que podem mais não ser do que disparate substantivo no que respeita aos processos psicológicos ou sociológicos reais. E interessante notar que, já em tempos recuados, Glanzer e Glaser (1959) escreviam:
A large number of papers deal with the expected number and the distributions of various configurations on the basis of chance (...) It has importance in evaluating the results of the analysis of configurations. For example, if a group has three isolates, it is of interest to discover how often this could have arisen by chance. However, a psychological theory or rationale to dictate the choice of configurations for study and to indicate why there should be departures from chance ordering has not been developed (p. 323);
e os insuspeitos Holland e Leinhardt (1970) não hesitaram em afirmar:
The most general import of these mathematical models is that they demonstrate how complex networks can be the result of interdependencies among interpersonal sentiment relations. Nonetheless, while meaningful theoretical insights can result from expressing social theory mathematically, these are not sufficient in themselves to argue for the acceptance of the theory. It still remains for empirical verification to help ns distinguish formal theory from formal nonsense; in this effort graph theory, because of its deterministic quality, has limited use. For example, a statement which implies that a group cannot be balanced if a line between two points serves to link two otherwise disconnected components, may follow logically from axioms of graph theory; it does not make much sense in the logic of empirical sociology (p. 492; itálico meu).
A crítica de Holland e Leinhardt às possíveis implicações absurdas da aplicação cega da teoria dos grafos ao modelo de equilíbrio estrutural de Heider vai no sentido do que acima se disse acerca das suas limitações, com ou sem teoria dos grafos a formaliza-la.
Por exemplo, os modelos até hoje construídos conduzem a um equilíbrio estocástico numa rede completamente conectada (é também o caso do modelo CONSTRUCT de Carley, acima referido). Ora, esse equilíbrio parece ser uma assimptota puramente formal, sem correspondência num mundo social em permanente mutação e marcado por permanentes conflitos e alterações muitas vezes estruturais. O próprio modelo de Carley fixa K, e não atende ao facto mais premente no mundo real: o incremento permanente de K a uma velocidade sem par na história do Homo sapiens — refiro-me concretamente à inovação científica e tecnológica. O que significa que o modelo de Carley está desenhado para pequenos mundos sociais fechados, como aliás é empiricamente demonstrado no seu trabalho (Carley, 1990). Ou seja, é um modelo exactamente no sentido a que acima se referiu: concentra-se numa gama limitada de fenómenos, não tenta explicar o universo, muito em consonância com a injunção popperiana de as ciências sociais produzirem modelos estáveis e de gama limitada (Popper, 1957). Por outro lado, os modelos atendem sobretudo ao problema da constituição de ligações entre actores sociais e, como fazem notar Banks e Carley (1996), é minimizado o problema da destruição ou anulação dessas ligações, ou seja, as consequências, para a dinâmica da rede social, da anulação de arcos significativos. Abordei esta questão na dinâmica de um grupo de primatas, com a remoção temporária de um a grupai e a sua reintrodução no grupo, seguida da introdução de um novo actor social desconhecido. As consequências destas manipulações da rede social perduraram, e os seus efeitos eram drasticamente visíveis dez anos depois (Soczka, 1984). No caso dos grupos humanos, estamos obviamente perante factores bem mais complexos do que no caso da etologia social de primatas acima citado, como o demonstram os programas de investigação sobre as redes sociais e as redes de suporte em meio urbano. Um dos casos mais flagrantes de alteração de redes sociais é o realojamento de habitantes de áreas degradadas em novos complexos de habitação social. Muitas vezes, antigas e fortes ligações sociais, porventura organizações comunitárias inteiras, são desmanteladas pelos assim chamados imperativos da política de realojamento, que muito frequentemente não correspondem senão aos imperativos a curto prazo das forças políticas autárquicas. Um caso recente é o dos realojamentos de famílias residentes no Bairro da Liberdade, em Lisboa, onde laços de 40 anos foram desfeitos pelo realojamento forçado em bairros novos e distantes, sem preocupações das entidades responsáveis por um estudo prévio das redes sociais existentes e muito menos das consequências da fragmentação dessas redes. Estudos prévios à acção de realojamento demonstram a natureza e importância das redes tecidas no bairro ao longo de décadas (Borges, 1994); estudos catamnésicos da mesma população já em situação de realojamento demonstram o impacte negativo da fragmentação das redes sociais pré-existentes (Bastos, 1997). Em nenhum destes estudos foi, no entanto, feita uma ARS formal da comunidade e, tanto quanto sabemos, o único estudo em larga escala alguma vez efectuado em Portugal com modelos matemáticos de ARS foi o caso da Musgueira Sul, onde foi realizado um levantamento extensivo das redes interfamiliares das 3500 pessoas residentes, e os resultados comunicados à autarquia no sentido expresso de constituir a base de decisão para uma acção de realojamento a curto prazo que fragmentasse o menos possível as redes existentes (Soczka et al, 1989).
A formalização matemática desenvolvida ao longo de 50 anos para a análise das redes sociais está longe de ser um mero exercício de estilo. Desenvolveram-se instrumentos matemáticos preciosos para a ARS que, como todos os instrumentos, em si mesmos estão para lá do juízo de valor. Podem, isso sim, é ser absurdas as suas utilizações ou as interpretações dos seus resultados, e essa responsabilidade recai puramente sobre os ombros dos cientistas sociais, não sobre os modelos de análise matemática como tais. A ARS percorreu já um longo caminho desde os tempos de Moreno (e não foi o próprio Moreno quem levou até aos extremos do absurdo a sociometria nascente, quando pretendeu ideologicamente transformar numa revolução social à escala planetária?). Muito há ainda certamente a percorrer, não só do ponto de vista do desenvolvimento de algoritmos como, sobretudo, da integração entre algoritmos, investigação empírica e integração teórica em ciências sociais.
Referências
Alba, R. D. (1973). A graph-theoretic definition of a sociometric clique. Journal of Mathematical Psychology, 3,113-126. [ Links ]
Bales, R. F. (1950). Interaction process analysis. Massachusetts: Addison-Wesley.
Banks, D. L., & Carley, K. (1996). Models for network evolution. Journal of Mathematical Psychology, 21 (1-2), 173-196.
Bastos, J. G. P. (1997). Investigação estrutural-dinâmica sobre a (trans)formação da identidade de lugar num grupo de idosos em situação de translocação heteronómica. CNIG: Lisboa.
Borgatti, S. R, Everett, M. G., & Freeman, L. C. (1997). UNICETIV. Analytic Technology, Col., SC.
Borges, M. J. (1994). Mudança em perspectiva: Redes psico-sociológicas e efeito de propinquidade no Bairro da Liberdade. Monografia de Licenciatura em Psicologia Social. Lisboa: ISPA.
Bronfenbrenner, U. (1945). " The measurement of sociometric status, structure and development", Sociometric Monographs, 6.
Carley, K. (1990). Group stability: A sócio-cognitive approach. Advances in Group Processes, 7,1-44.
Cartwight, N. e Harary, F. (1956). "Structural balance: a generalization of Heider's theory", Psychological Review, 63: 277-293.
Chase, I. D. (1974). Models of hierarchy formation in animal societies", Behavioral Science, 19: 374-382.
Chase, I. D. (1980). "Social process and hierarchy formation in small groups", American Sociological review, 45: 905-924.
Criswell, J. H. (1946). The measurement of reciprocation under multiple criteria of choice. Sociometry, 9, 126-127.
Davis, J. A. (1967). Clustering and structural balance. Human Relations, 20, 181-187.
Davis, J. A., & Leinhardt, S. (1972). The structure of positive interpersonal relations in small groups. In J. Berger (Ed.), Sociological theories in progress (pp. 218-251). Boston: Houhton Mifflin.
Doreian, P. (1970). Mathematics and the study of social relations. Londres: Weidenfeld and Nicholson.
Faucheux, C., & Moscovici, S. (1960). Études sur la créativité des groupes: Tâches, structures de communication et réussite. Bulletin du CERP, 9,11-12.
Festinger, L. (1949). The analysis of sociograms using matrix álgebra. Human Relations, 2, 153-158.
Festinger, L. (1954). A theory of social comparison processes. Human Relations, 7,117-140.
Festinger, L. (1957). A theory of cognitive dissonance. Londres: Peterson.
Fienberg, & Wasserman, S. (1981). Catégorial data analysis of single sociometric relations. In S. Leinhardt (Ed.), Sociological methodology (pp. 156-192).
Fisher, C. S. (1975). Toward a subcultural theory of urbanism. American Journal of Sociology, 80,1319-1341.
Fisher, C. S. (1976). The urban experience. Nova Iorque: Harcourt Brace.
Fisher, C. S. (1982). To dwell among friends: Personal netiuorks in toiun and city. Chicago: University of Chicago Press.
Freeman, L. C. (1979). "Centrality of social networks", Social Networks, 1: 215-239.
Glanzer, M., & Glaser, R, (1959). Techniques for the study of group structure and behaviour. Psychological Bulletin, 56, 317-332.
Hararay, F., Norman, R. Z., & Cartwright, D. (1965). Structural models: An introduction to the theory of directed graphs. Nova Iorque: Wiley.
Heider, F. (1946). Attitudes and cognitive organization. Journal of Psychology, 21,107-112.
Heider, F. (1958). The psychology of interpersonal relations. Nova Iorque: Wiley.
Holland, P. W., & Leinhardt, S. (1970). A method for detecting structure in sociometric data. American Journal of Sociology, 70,492-513.
Holland, P. W., & Leinhardt, S. (1971). Transitivity in structural models of small groups. Comparative Group Sudies, 2,107-124.
Holland, P. W., & Leinhardt, S. (1975). The statistical analyis of local structure in social networks. In D. Heise (Ed.), Sociological methodology (pp. 1-45).
Holland, P. W., & Leinhardt, S. (1977). A dynamic model for social networks. Journal of Mathematical Sociology, 4,314-318.
Holland, P. W., & Leinhardt, S. (1981). An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association, 76,33-65.
Holland, P. W., Laskey, K. B., & Leinhardt, S. (1983). Stochastic blockmodels. Social Networks, 5,109-137.
Homans, G. C. (1950). The human group. Nova Iorque: Harcourt Brace.
Hubbel, C. H. (1965). An input-output approach to clique detection. Sociometry, 28, 277-299.
Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18, 39-43.
Katz, L.; Tagiuri, R. e Wilson, T. (1958). "A note on estimating the statistical significance of mutuality", The Journal of General Psychology, 58: 97-193.
Knocke, D., & Burke, P. J. (1980). Log-linear models. Thousand Oaks, CA: Sage.
Langeheine, R. (1976). SDAS: A sociometric data analysis system. Kiel: Christian-Albrecht Universität.
Lazarsfeld, P. e Merton, R. (1954). Friendships as social processes", in Berger (Ed), Freedom and control in modern society, Octagon Books.
Lewin, K. (1947). Frontiers in group dynamics. Human Relations, 1, 2-38.
Lewin, K. (1951). Field theory in social sciences. Nova Iorque: Harper and Row.
Lorrain, E, & White, H. C. (1971). Structural equivalence of individuals in social networks. Journal of Mathematical Sociology, 1,49-80.
Luce, R. D. (1950). Connectivity and generalized cliques in sociometric group structure. Psychometrika, 15,169-170.
Luce, R. D., & Perry, A. D. (1949). A method of matrix analysis of group structure. Psychometrika, 14, 95-116.
Maisonneuve, J. L. (1966). Psycho-sociologie des affinités. Paris: PUE
Moreno, J. L. (1934). Who shall survive?, Beacon House. Edição francesa: Les fondements de la sociométrie, PUF, Paris, 1953.
Moreno, J. L. (1938). Who shall survive? Nova Iorque: Beacon House.
Moreno, J. L., & Jennings, H. (1938). Statistics of social configurations. Sociometry, 1, 342-374.
Pattison, P. E. (1993). Algebraic models for social networks, Cambridge University Press.
Popper, K. (1957). The poverty ofhistoricism. Londres: Routledge.
Richards, W., & Seary, A. (1997). Introduction to eigen analysis ofnetivorks. INSNA Sunbelt XVII, San Diego. Retirado da Internet: http://www.sfu.ca/-richards/wdr97.htm
Roberts, F. S. (1976). Discrete mathematical models. Nova Jérsia: Prentice-Hall.
Sanil, A., Banks, D., & Carley, K. (1995). Models for evolving fixed node networks: Model fitting and model testing. Social Networks, 17, 65-81.
Seeley, J. R. (1949). The net of reciprocal influence: A problem of treating sociometric data. Canadian Journal of Psychology, 3, 234-240.
Soczka, L. (1974). "Éthologie sociale et sociométrie", Behaviour, 50: 254-269.
Soczka, L. (1984). Etologia social e sociometria: Estudo da estrutura e dinâmica de um grupo de Kra. Tese de Doutoramento em Ciências Biomécias. Porto: Universidade do Porto.
Soczka, L. (1994). Ensaios de etologia social. Lisboa: Fim de Século.
Soczka, L. (1995). Para uma sócio-etologia do insucesso escolar: Uma abordagem num contexto de bairro-de-lata. Psicologia, X, 31-64.
Soczka, L., Machado, P, & Freitas, M. J. (1989). Realojamento de famílias da Musgueira Sul no bloco 128 do plano geral de urbanização do Alto do Lumiar (Rei. 78/90). Lisboa: LNEC / GES.
Soczka, L; Vila-Real, A e Brito, M. D. (1997). Análise descritiva dos padrões de utilização do tempo diário em crianças e pré-adolescentes, Relatório para o Programa Praxis XXI, CNIG.
Wasserman, S. (1980). Analysing social networks as stochastic processes. Journal of the American Statistical Association, 75, 280-294.
Wasserman, S. e Iaccobucci, D. (1988). "Sequential social network data", Psychometrika, 53: 261-282.
Wasserman, S., & Faust, K. (1994). Social netiuork analysis. Cambridge: Cambridge University Press.
White, H. C.; Boorman, S. e Breiger, R. L. (1976). "Social structure from multiple networks", American Journal of Sociology, 81: 730-779.
Notas
1Com efeito, num dígrafo, para cada nó verifica-se um valor de entrada e um valor de saída, relativos ao número de nós com os quais se conecta e que a ele se conectam. Este valor pode ser nulo, como é evidente. Designa-se aqui o conceito de entrada ou recepção (input) por I-conexão, e o de saída ou emissão (output) por O-conexão. Paralelamente, I-grau e O-grau, designam, respectivamente, o número de arcos que terminam em n:eo número de arcos que nesse nó têm origem.
2De weighted-graphs, de acordo com a proposta de Roberts (1976). Os grafos sinalizados ou S-grafos, em que as valências assumem os valores discretos -1 ou +1, são casos particulares de W-dígrafos.
3Luce e Perry (1949) designaram por antimetria a ausência de reciprocidade (simetria) numa relação entre os actores sociais i e j. Ou seja, ni → n ou n → ni mas não ambos.
4Paralelamente ao índice de Katz, outras medidas e técnicas foram propostas, nomeadamente o já referido índice de Hubbel (além de complexificações do modelo propostas colateralmente pelo próprio Katz, no seu artigo de 1953), Hubbel (1965) generaliza o método de Seeley (1949), construindo um modelo de input-output para detecção de cliques, e deriva índices de estatuto para cada actor, pegando na equação básica de Seeley e adicionando-lhe uma constante, correspondente ao que designou pela "contribuição exógena" de cada actor para o seu próprio prestígio.
5Por "pontos", na terminologia destes autores, leia-se "nós".
6Para uma dada díade (i, j), obtém-se uma tabela de contingência 2x2 em que Yij00=(1-Xij)(1-Xji), Yij10 = Xij(1-Xij), Yij01 = Xji(1-Xij) e Yij11
7Muitas vezes designados por pij, como em Fienberg e Wasserman (1981) ou Banks e Carley (1996).
8A não confundir com o conceito de coesão acima referido, que se prende à conectividade ou n-conectividade
9A técnica de blockmodeling vem dos trabalhos de White e colaboradores (1976), que se dedicaram à edificação de uma álgebra dos papéis sociais (cf. Pattison, 1993; Wasserman e Faust, 1994).
10O package vocacionado para o processamento de redes sociais UCINET IV de Borgatti, Everett e Freeman (1991) correlaciona directamente sociomatrizes, e encontra-se instalado no CNIG.
11Por exemplo, o modelo prediz conflito num casal em que os cônjuges votem ou pertençam a partidos políticos distintos, ou entre amigos por serem adeptos de clubes de futebol diferentes. E que para ultrapassar o conflito só haveria uma saída: um dos membros do casal converter o outro à sua crença partidária e um dos amigos converter o outro à sua crença desportiva, ou passarem ambos a não gostar do partido ou clube em questão. Caso contrário, o casal divorcia-se e os amigos deixam de ser amigos? Mal estaria o mundo, ou pior já está, se as coisas fossem mesmo assim.












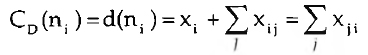
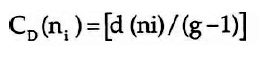
 , para um grau de liberdade, o que equivale ao quadrado do desvio normal reduzido. Para o caso geral, o Teorema de Mood (1974) prova-nos que a soma dos quadrados de variáveis independentes aleatórias normais estandardizadas tem uma distribuição de qui-quadrado com um número de graus de liberdade igual ao número de termos da soma.
, para um grau de liberdade, o que equivale ao quadrado do desvio normal reduzido. Para o caso geral, o Teorema de Mood (1974) prova-nos que a soma dos quadrados de variáveis independentes aleatórias normais estandardizadas tem uma distribuição de qui-quadrado com um número de graus de liberdade igual ao número de termos da soma.