Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Portugaliae Electrochimica Acta
versão impressa ISSN 0872-1904
Port. Electrochim. Acta vol.38 no.5 Coimbra jun. 2020
https://doi.org/10.4152/pea.202005313
ARTIGOS
Quantum Modeling and Molecular Dynamic Simulation of some Amino Acids and Related Compounds on their Corrosion Inhibition of Steel in Acidic Media
Bello Abdullahi Umar*, Adamu Uzairu and Gideon Adamu Shallangwa
Department of Chemistry, Ahmadu Bello University, Zaria, Nigeria
ABSTRACT
The inhibition performance of twenty-five amino acids and related compounds was studied by theoretical techniques. The effect of the acidic solution was considered on the molecular dynamics simulation, and the calculated binding energies for most of the inhibitors was ?100 kcal mol−1, suggesting chemisorptive interactions. Density Functional Theory (B3LYP/6-31G*) quantum substance chemical study was utilized to discover the upgraded geometry of the inhibitors. Also, a linear quantitative structure-activity relationship (QSAR) model was built by Genetic Function Approximation (GFA) method, to run the regression analysis and build up connections between various descriptors and the experimental inhibition efficiencies. The prediction of corrosion efficiencies of these inhibitors nicely matched the experimental measurements. The statistical parameters are: R2train = 0.963814, R2adjusted = 0.95317, Q 2L100= 0.921998 and R2test = 0.973421, which indicates that the model was excellent. The proposed model has great dependability, strength, and consistency on checking, with inward and outside approval.
Keywords: amino acids; quantum chemical calculation; molecular dynamics simulation; QSAR; GFA; DFT (B3LYP/6-31G*).
Introduction
Pipelines assume a critical part everywhere throughout the world as equipment for transporting gases and fluids over long distances, from their sources to shoppers. So, corrosion issue exists in the oil business at each phase of creation, from the extraction to refining and storage, preceding use, which requires the utilization of corrosion inhibitors (5). Numerous strategies, including experimental and theoretical methodologies, have been typically utilized to consider the performance of amino acids as corrosion inhibitors. In spite of the fact that experimental measures, for example, weight reduction technique, potentiodynamic polarization, electrochemical impedance spectroscopy (EIS), etc. (6), are the most conventional methods to test the inhibition performance, they are costly and tedious, since huge scale trial tests have been completed. Theoretical methods, which can defeat these deficiencies, have gained scientists' incredible consideration as of late. Quantum chemical studies have officially turned out to be extremely helpful in deciding the atomic structure and explaining the electronic structure and reactivity (8). Consequently, it has turned into a typical practice to complete quantum chemical calculations in corrosion studies. The idea of surveying the productivity of a corrosion inhibitor with the assistance of computational science is to look for compounds with wanted properties utilizing chemical intuition and experience into a mathematically quantified and computerized form. Once a connection between the structure and activity or property is discovered, any number of compounds, including those not yet synthesized, can be promptly screened utilizing computational procedures (9), a set of mathematical equations which are capable of representing accurately the chemical phenomenon under study (10). Being utilized as a part of science amid the second half of the twentieth century as an expanded measurable examination (11), the quantitative structure-activity relationship (QSAR) technique has recently achieved an uncommon status, formally confirmed by European Union as the fundamental computational apparatus (inside the purported "in silico" approach) for the administrative appraisals of chemicals by methods for non-testing strategies (12). A structure-activity relationship is generally defined as a mathematical relationship between a property of a chemical (its activity) and a combination of molecular parameters. Normally, the main thrust behind the development of any QSAR is the induction of major conditions which will, somehow, characterize corrosion inhibition efficiency as a function of physical and chemical descriptors characterizing the inhibitor molecules.
Moreover, to consider the adsorption conduct of amino acids onto the metal surface, molecular dynamics simulation was used to research the adsorption configuration and adsorption strength of amino acids onto the metal surface (13). For instance, Fu (14) researched the inhibition behavior of four amino acids compounds on a Fe(110) surface in an aqueous solution, and found that they could be absorbed onto the iron surface through the heteroatoms and a heterocyclic ring. Though some useful information has been obtained from these studies, there still exists some disparity between the theoretical adsorption model and realistic inhibition systems. Various factors, such as the adsorption of the solvent molecules, the protonation of the inhibitor molecules, and the affection of the acidic solution, which would greatly influence the adsorption behaviors of the amino acid compounds, should also be considered in the molecular dynamics simulation.
In this work, molecular simulation studies were performed to simulate the adsorption of the amino acids on an iron surface. Also, the goal of this study is to encapsulate knowledge about the selected amino acid which is used as corrosion inhibitor for iron in molar hydrochloric (HCl) acid.
Materials and methods
Materials
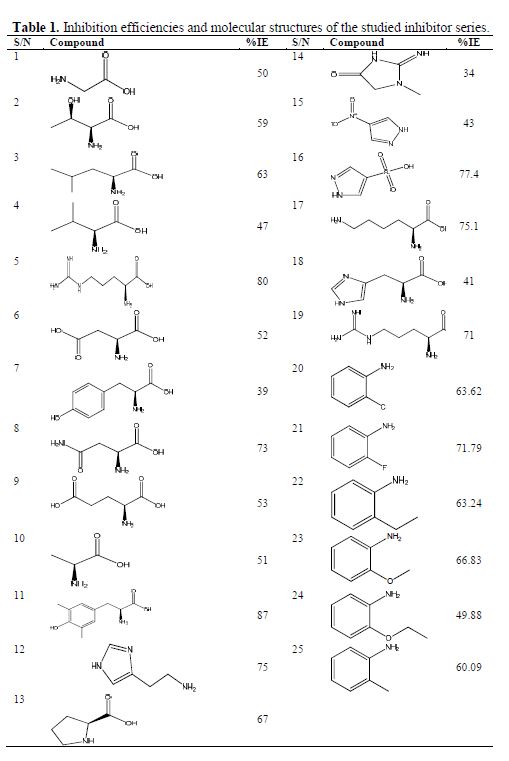
Twenty-five amino acids and related molecules were collected from the literature (15-17) and investigated in the present study, and their molecular structures and inhibition efficiencies are shown in table 1. The inhibition efficiencies of all these molecules were obtained by potentiodynamic polarization curves in 1 mol/L hydrochloric acid with 0.01 mol/L concentration of the amino acids against iron corrosion.
Methods
Computational details
Geometry optimization was performed using density functional theory (DFT). The Becke’s Three Parameter Hybrid Functional using the Lee-Yang-Parr correlation functional theory was selected for the calculations. Calculations were done using the 6-31+G(d) basis set.
All optimization calculations were done using the Spartan 14v.1.1.0 software. Schematic structures were drawn using the Chemdraw ultra 12.0. The quantum chemical descriptors were calculated using the Spartan’14 V.1.1.0 quantum chemistry package and Material studios 8.0.
Molecular dynamics simulation
The molecular dynamics (MD) simulation was performed using Forcite module of Materials Studio 8.0 program developed by Accelrys Inc (19). The whole system was performed at 298 K, controlled by the Andersen thermostat, NVE ensemble, with a time step of 1.0 fs, simulation time of 2000 ps, and 5000 Number of steps using the compass force field. The MD simulation was carried out in a simulation box (24.823752A×24.82752A×45.268509A) with periodic boundary conditions. The box includes a Fe slab, an acid solution layer and an inhibitor molecule. Iron (Fe (110)) was selected as the studied surface, since it was density packed and it was the most stable (18). The iron crystal contained ten layers, and seven layers near the bottom were frozen. The density of the acidic solution layer was set as 1.0 g/cm-3. Non-bond interactions, van der Waals and electrostatic were set as atom-based summation method and Ewald summation method, respectively.
Quantitative structure-activity relationship (QSAR)
Quantitative structure-activity relationship (QSAR) was built by the Genetic Function Approximation to correlate the inhibition efficiencies and the molecular structure characteristics of the amino acids’ molecules, which were freely available in Materials Studio 8.0. All calculations were performed using the Microsoft office Excel 2013.
The GFA algorithm approach has a number of important advantages over other standard regression analysis techniques. It builds multiple models rather than a single model (21). It automatically selects which features are to be used in the models, and it is better at discovering combinations of features that take advantage of correlations between multiple features (20). GFA incorporates Friedman’s lack-of-fit (LOF) error measure, which estimates the most appropriate number of features, resists over fitting, and allows control over the smoothness of fit. Also, it can use a larger variety of equation term types in the construction of its models and finally, it provides, through the study of the evolving models, additional information not available from standard regression analysis.
Training and test set
The training set is comprised of molecules used in the model development, while the test set is made up of molecules not used in building the model; they were used in the external validation of the model generated by the training set. The data-set for the inhibition efficiency was split into the training set and the test set. 18 of the data-sets were used as a training set, while the remaining 7 were used as a test set in line with the optimum splitting pattern of the data-set in the QSAR study (4), as shown in table 1. The training set was used to generate the model, while the test set was used to evaluate its predictive abilities.
Model validation
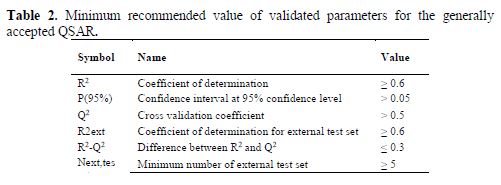
Internal and external validation parameters were used to evaluate the reliability and predictive ability of the models. The validation parameters were compared with the standard for the generally acceptable QSAR model, as reported in table 2.
Internal validation parameters
Lack of fit (LOF)
A “fitness function” or lack of fit (LOF) was used to estimate the quality of the model, so that the best model receives the best fitness score. The error measurement term is determined by equation (1):

where ‘c’ is the number of basic functions (other than the constant term); ‘d’ is the smoothing parameter (adjustable by the user); ‘M’ is the number of samples in the training set; LSE is the least squares error; and ‘p’ is the total numbers of the features contained in all basic functions (22).
Coefficient of multiple determination (R2)
To assess the goodness-of-fit, the coefficient of multiple determination is used. R2 estimates the proportion of the variation in the response that is explained by the predictor:
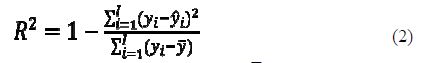
where yi is the observed dependent variable, ??¯ is the mean value of the dependent variable and ??^ is the calculated dependent variable.
If there is no linear relationship between the dependent variable and the descriptors, then R2 = 0.00; if there is a perfect fit, then R2 = 1.00. R2 values higher than 0.5 indicate that the explained variance by the model is higher than the unexplained one (27).
Adjusted R2 (R2adj)
The value of R2 can generally be increased by adding additional predictor variables to the model, even if the added variable does not contribute to reduce the unexplained variance of the dependent variable. It follows that R2 should be used with caution. This can be avoided by using another statistical parameter: the so-called adjusted R2 (R2adj)
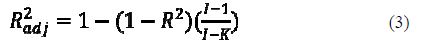
R2adj is interpreted similarly to the R2 value, except that it takes into consideration the number of degrees of freedom (26).
The value of R2adj decreases if an added variable to the equation does not reduce the unexplained variable.
Standard error of estimate (SEE)
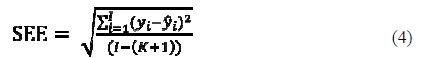
The smaller the value of SEE is, the higher the reliability of the prediction. However, it is not recommended to have the standard error of estimate smaller than the experimental error of the corrosion data, because it is an indication of an over fitted model.
F-value
The F-value is determined using equation 5:
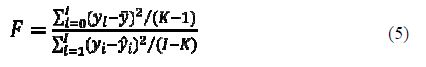
The higher the F-value, the greater the probability that the equation is significant (23).
Cross-validation squared correlation coefficient R2 (R2cv)
Cross-validation squared correlation coefficient R2 (LOO-Q2) is calculated according to the formula:
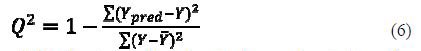
where Ypred and Y indicate predicted and observed activity values, respectively, and ??¯ indicates the mean activity value. A model is considered acceptable when the value of Q2 exceeds 0.5 (24).
In the case of this research, external validation techniques (LMO-Leave Many Out) were applied, in which the 7 compounds of the test set were used for the external validation, and the predicted R2 for the validation was calculated using equation 2.
External validation parameters
Predicted R2 (R2pred)
The predictive R2 was calculated only based on molecules not included in the training set (test set). Models are generated based on training set compounds, and the predictive capacity of the models was judged based on the predictive R2 (R2pred) value which was calculated using equation 7:
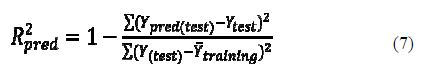
where ??pred(????????) and ?????????? indicate predicted and observed activity values respectively of the test set compounds and ??¯???????????????? indicates the mean activity of the training set. For a QSAR model, the value of R2pred should be more than 0.5. All the calculated statistical parameters agree with the criteria reported in table 2.
Applicability domain
The applicability domain (AD) of the QSAR model was used to verify the prediction reliability, identify the problematic compounds and predict the compounds with acceptable activity that fall within this domain. The most common methods used for the determination of the AD of QSAR models have been described by Gramatica that used the leverage values for each compound. The leverage approach allows the determination of the position of new chemicals in the QSAR model, i.e., whether a new chemical will lie within the structural model domain or outside of it. The leverage approach along with the Williams Plot is used to determine the applicability domain in all QSAR models. To construct the William Plot, the leverage hi for each chemical compound – in which QSAR model was used to predict its property – was calculated according to the following equation:

where x refers to the descriptor vector of the considered compound and X represents the descriptor matrix derived from the training set descriptor values. The warning leverage (h*) was determined as:

where N is the number of training compounds and p is the number of descriptors in the model.
Results and discussion
Molecular dynamic simulation study
To get further information about the interaction between the amino acids and related compounds and the Fe surface, molecular dynamics (MD) simulation was performed. In order to build a more reliable model, both water and hydrogen chloride were added to the solution layer for the studied system. In 1 mol/L hydrochloric acid solution, the ratio of water molecules and hydrogen chloride was 500/9. The system was constructed using the amorphous cell module, and the geometry optimization of the system was made. Then, the dynamics process was carried out until equilibrium was reached when both temperature and energy of the system were balanced. Fig. 1 shows the complex molecular dynamic system of inhibitor-14. All other systems for the inhibitors were similarly studied.
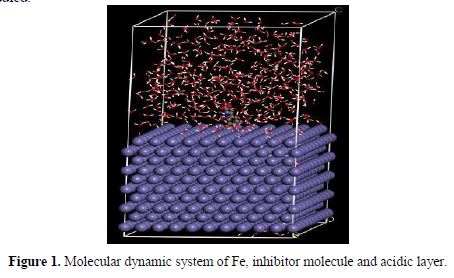
The strength of corrosion inhibitors absorbed onto the iron surface can be expressed by the binding energy, so it will be very interesting to study the binding energies of amino acids absorbed onto the iron surface. The binding energy in the solution can be calculated by the following equations (28):
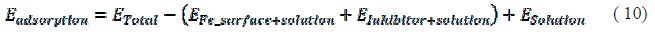
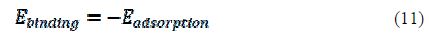
where ETotal was the total energy of the system, which includes iron crystal, the adsorbed inhibitor molecule and solution; EFe-surface+solution and Einhibitor+solution were the energies of the system without the inhibitor and the system without the iron crystal, respectively; and ESolution was the energy of the solution in kcal/mol. The calculated adsorption energies and binding energies were listed in table 3.
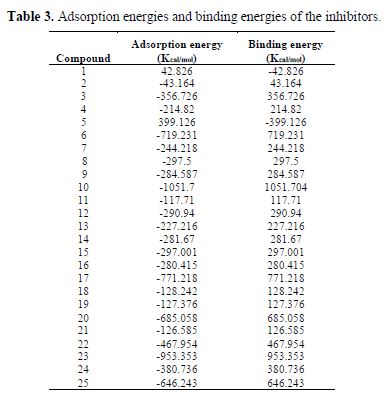
In table 3, adsorption and binding energies calculated between Fe (110) surface and twenty-five amino acids and related compounds, using equation 10 and 11, utilizing Molecular dynamics simulations approach, are given.
Adsorption energy is characterized as the energy released when the inhibitor molecule was adsorbed onto the metal surface. As said in equation 11, the binding is the negative value of the adsorption energy. The most stable low energy configurations obtained for the adsorption of Inhibitor-14 on Fe (110) in 1 M HCl are exhibited in Fig. 2. All different systems for the inhibitors were similarly examined.
It is apparent from the molecular structures of the examined Azoles derivatives that these molecules contain various lone pair electrons on N and S atoms, as well as π-aromatic frameworks.
Therefore, giving the lone pair electrons on heteroatoms to the empty d orbitals of iron, specified inhibitors can form a stable coordination bonding. It can be noticed from Fig. 2 that the inhibitor is adsorbed nearly parallel to the Fe (110) surface, with the assistance of the donation of π electrons of the rings appearing in the structures of the particles and the lone pair of the heteroatoms.
It was accounted for in many investigations that the primary mechanism of the interaction between corrosion inhibitors and iron is by adsorption. In this way, the adsorption energies calculated via molecular dynamics simulations approach can give us an immediate understanding to compare the anticorrosive performances of the inhibitor molecules.
It is seen from table 3 that the calculated adsorption energies of the examined inhibitors on the iron surface are generally negative values, with the exception of six of the inhibitors (1 and 5) that appear to be positive, which may be expected due to the solvent impact. These negative values denote that the adsorption happening amongst metal and inhibitors could happen spontaneously.
The largest negative adsorption energy indicates that the system is most stable and that adsorption is exceptionally strong.
Then again, a positive and larger value of the binding energy implies that the corrosion inhibitor binds with the Fe (110) surface more easily and firmly (3).
Quantitative structure-activity relationship (QSAR)
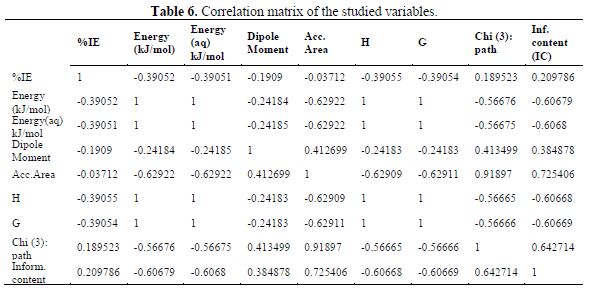
Usually, quantitative structure and activity relationships using the GFA method are done in three stages. The first stage is represented in table 4. The second and third stages, correlation matrix, and regression parameters are presented in Tables 6 and 5, respectively.
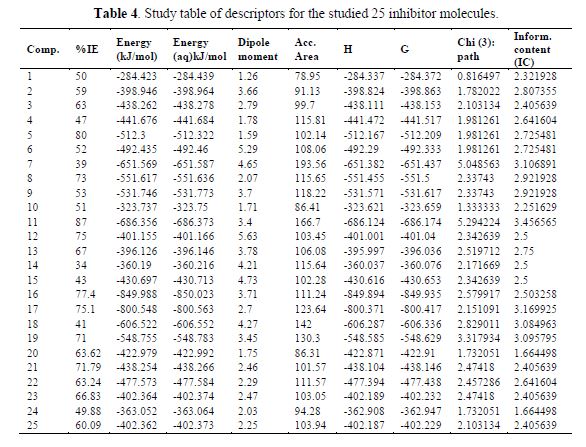
A univariate analysis is performed on the inhibition efficiency data from table (table 4), and the result of the univariate analysis is presented in table 5. The univariate analysis is a tool that assesses the quality of the data available and its suitability for next statistical analysis. The data in table 5 show acceptable normal distribution. The normal distribution behavior of the studied data was confirmed by the values of standard deviation, mean absolute deviation, variance, skewness and kurtosis presented in table 5. A description of these parameters has been reported elsewhere (25).
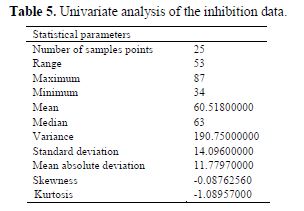
table 6 contains a correlation matrix, which gives the correlation coefficients between each pair of columns included in the analysis. Correlation coefficients between a pair of columns approaching +1.0 or -1.0 suggest that the two columns of data are not independent of each other (7). The correlation matrix can help to identify highly correlated pairs of variables, and thereby identify redundancy in the data set. After constructing the correlation matrix in table 6, four (4) QSAR generated GFA models for %IE of the compounds are presented below. Out of the 4-models, model-1 was selected as the best for predicting the inhibition efficiency of the studied inhibitors, based on the fact that it has the best statistical parameters. The validation parameters of the models agree with the standard reported in table 2.

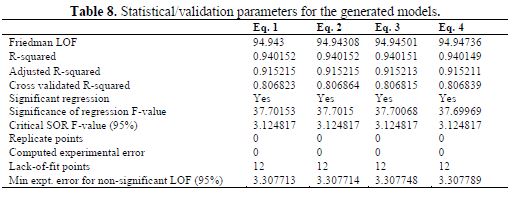
Statistical/Validation parameters for the generated models
Statistical parameters for the internal validation of all the 4 models were calculated and presented in table 8. There is a good agreement of the validation parameters with the standard reported in table 2.
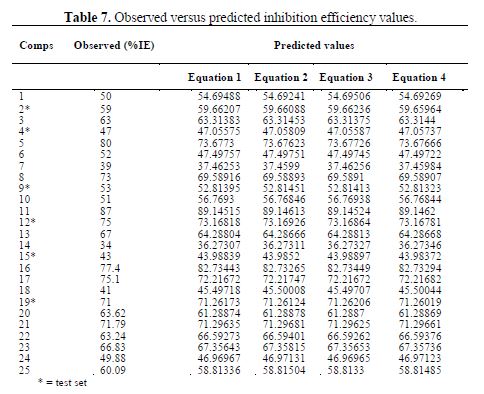
Comparison of the observed and predicted %IE
The comparison of the predicted inhibition efficiency of the models with the experimental values for the training and test sets is presented in table 7.
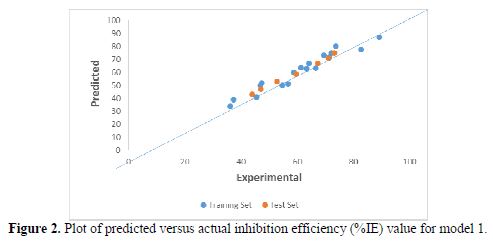
Plot of predicted versus actual inhibition efficiency (%IE) values
The plot of the predicted versus actual (%IE) values for model-1 is presented in Fig. 2.
Fig. 3 shows the Williams plot of standardized residuals against calculated leverages for both the training and test set.
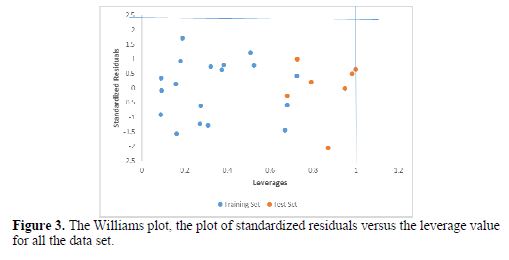
The leverages for every compound in the dataset were plotted against their standardized residuals, leading to the discovery of outliers and influential chemicals in the models. The applicability domain is established inside a squared area within ±3d bound for residuals and a leverage threshold h* is equal to 1.0 (N = 18 and p=5)n (1-2). From our result, it is evident that all the compounds of the training set and test set for the dataset were within the square area (table 8).
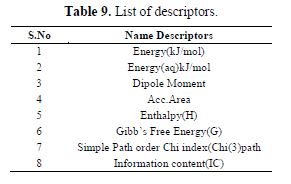
table 9 gives a list of all the descriptors used to develop the models used in the study.
The result of the GFA QSAR model is in conformity with the standard shown in table 3, as seen in equation 3. The closeness of coefficient of determination (R2) to its absolute value of 1.0 is an indication that the model explained a very high percentage of the response variable (descriptor) variation, high enough for a robust QSAR model. The high adjusted R2 (R2adj) value and its closeness in value to the value of R2 implies that the model has excellent explanatory power to the descriptors in it.
Also, the high Q2 value and its closeness to R2 revealed that the model was not over fitted. The high R2pred. is an indication that the model is capable of providing valid predictions for new molecules that fall within its applicability domain.
F value judges the overall significance of the regression coefficients. The high F value of the model is an indication that the regression coefficients are significant.
Furthermore, the equation contains five descriptors and each descriptor has a positive or negative coefficient attached to it.
These coefficients, along with the value of descriptor, have a significant role in deciding the overall inhibition efficiency of the inhibitor molecules.
Examination of equation 4 shows that the coefficients of each descriptor play an important role in deriving the inhibition efficiency.
From the point of view of inhibition of the molecules in terms of %IE values, the weight of a positive coefficient is very significant because it contributes towards an increased value of %IE.
table 10 shows the external validation of model 1, and table 11 shows the calculated ????????2.
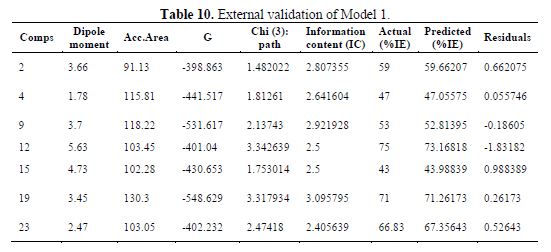
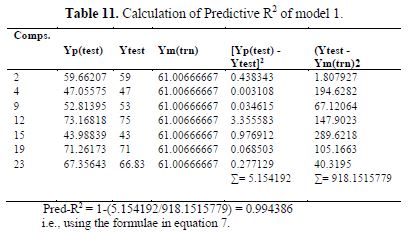
So, the descriptors with high weight positive coefficients are the most important, followed by descriptors with a low weight negative coefficient and, lastly, the descriptors with high weight negative coefficients.
On the basis of the coefficient values on the model, the associated descriptors are arranged in a sequence pertaining to their contribution towards overall inhibition efficiency of the inhibitors, in the following increasing order of inhibition efficiency towards steel corrosion.
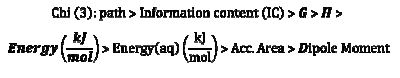
Conclusion
This research addresses the QSAR between a set of amino acids and related compounds, and their inhibition efficiency against steel corrosion. Our study developed four GFA-derived models, out of which the optimal model was selected on the basis of its superior statistical significance. The prediction of corrosion efficiencies of these compounds nicely matched the experimental measurements. The molecular surface interactions, estimated using molecular dynamics, suggest that inhibitors bind more strongly (chemisorption) in the presence of an aqueous acidic medium through the heteroatoms, carboxylic group, halogen atoms and through the aromatic ring. Therefore, this will provide a guide on designing more efficient corrosion inhibitors.
References
- OECD. Guidance document on the validation of (quantitative) structure–activity relationships ((Q)SAR) models. Organization for Economic Co-Operation and Development; 2007.
- Roy K, Kar S, Ambure P. On a simple approach for determining applicability domain of QSAR models. Chemometr Intell Lab Syst 2015;145:22-9.
- Obot IB, Kaya S, Kaya C, et al. Density Functional Theory (DFT) modeling and Monte Carlo simulation assessment of inhibition performance of some carbohydrazide Schiff bases for steel corrosion. Physica E: Low-dimensional Systems and Nanostructures. 2016;80:82–90.
- Patil SS. A least square approach to analyze usage data for effective web personalization. International Journal of Computer Engineering Research. 2011;2:68-74.
- Migahed MA. Corrosion inhibition of steel pipelines in oil fields by N,N-di(poly oxy ethylene) amino propyl lauryl amide. Progress in Organic Coatings. 2005;54(2):91-98.
- Zhang D, Cai Q, He X, et al. Inhibition effect of some amino acids on copper corrosion in HCl solution. Mater Chem Phys. 2008;112:353-358.
- Khaled KF, El-Sherik AM. "Using Molecular Dynamics Simulations and Genetic Function Approximation to Model Corrosion Inhibition of Iron in Chloride Solutions?. International Journal of Electrochemical Science. 2013;10022 – 10043.
- Kraka E, Cremer D. Computer design of anticancer drugs. J Am Chem Soc. 2000;122:8245–8264.
- Karelson M, Lobanov V. Quantum chemical descriptors in QSAR/QSPR studies. Chem Rev. 1996;96:1027–1043.
- Hinchliffe A. Chemical Modelling From Atoms to Liquids. John Wiley & Sons. New York. 1999.
- Chatterjee SA, Hadi AS, Price B. Regression analysis by examples. 3rd Ed. John-Wiley: New York, USA. 2000.
- Benigni R, Bossa C, Netzeva TI, et al. Collection and evaluation of QSAR Models for mutagenicity and carcinogenicity. European Commission-Join Reseach Center: Ispra, Italy. 2007; available online: http://ecb.jrc.it/qsar/publication/,accessed January, 2009.
- Khaled KF. Corrosion control of copper in nitric acid solutions using some amino acids – A combined experimental and theoretical study. Corros Sci. 2010;52:3225-3234.
- Fu J, Li S, Wang YL, et al. Computational and electrochemical studies of some amino acid compounds as corrosion inhibitors for mild steel in hydrochloric acid solution. J Mater Sci. 2010;45:6255-6265.
- Khaled KF, Hackerman N. Investigation of the inhibitive effect of orthosubstituted anilines on corrosion of iron in 1 M HCl solutions. Electrochim Acta. 2003;48:2715–2723.
- Hluchan V, Wheeler BL, Hackerman N. Amino acids as corrosion inhibitors in hydrochloric acid solutions. Mater Corros. 1988;39:512-517.
- Babic-Samardžija K, Lupu C, Hackerman N, et al. Langmuir. 2003;2:12187-12196.
- Khaled KF. Molecular simulation, quantum chemical calculations and electrochemical studies for inhibition of mild steel by triazoles. Electrochim Acta. 2008;53:3484-3492.
- Musa A, Jalgham R, Mohamad A. Molecular dynamic and quantum chemical calculations for phthalazine derivatives as corrosion inhibitors of mild steel in 1M HCl Corros Sci. 2012;56:176-183.
- Khaled K, Abdel-Shafi N. Int J Electrochem Sci. 2011;6:4077-4094.
- Accelrys to Release Enhanced Suite of Chemicals and Materials Modeling and Simulation Tools with Materials Studio(R) 4.1, in: Business Wire, New York, United States, New York, 2006, pp. 0-n/a.
- Kunal R, Roy PP, Paul S, et al. Molecules. 2009;14:1660-1701.
- Sofie Van Damme. “Quantum Chemistry in QSAR, Quantum Chemical Descriptors, use, benefits and drawback”. Thesis. Department of inorganic and physical chemistry, Faculty of Science, Universiteit Gent (2009), p 39.
- Wold S, Eriksson L. In Chemometrics Methods in Molecular Design; van de Waterbeemd H. Ed VCH, Weinheim, Germany, 1995, pp. 309-318.
- Khaled KF. Corros Sci. 2011;53:3457-3465.
- Jalali-Heravi MJ, Kyani A. Use of computer-assisted methods for the modeling of the retention time of a variety of volatile organic compounds: A PCA-MLR-ANN approach. Journal of Chemical Information and Modeling. 2004;44:1328–1335. http://dx.doi.org/10.1021/ci0342270.
- Brandon-Vaughn OKA. Comprehensive R archive network (CRAN). 2015. Retrieved from http://CRAN.R-project.org
- Pradip BR, Sathish P. Rational design of dispersants by molecular modeling for advanced ceramics processing applications, KONA 2004;22:151-158.
Received October 25, 2017; accepted March 13, 2018
* Corresponding author. E-mail address: abdallahbum@yahoo.com