Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Portuguesa de Educação
versão impressa ISSN 0871-9187
Rev. Port. de Educação vol.32 no.2 Braga dez. 2019
https://doi.org/10.21814/rpe.16121
ARTIGOS
Conhecimento de estatística bivariada de futuros professores portugueses dos primeiros anos
Knowledge of bivariate statistics by Portuguese prospective primary school teachers
Conocimiento de estadística bivariada por futuros profesores portugueses de educación primaria
José António Fernandesi
María M. Geaii
Paulo Ferreira Correiaiii
iUniversidade do Minho, Portugal
iiUniversidade de Granada, Espanha
iiiEscola Secundária de Barcelos, Portugal
RESUMO
O objetivo deste trabalho é analisar o conhecimento estatístico de uma amostra de futuros professores dos primeiros anos escolares quando resolvem uma tarefa envolvendo uma distribuição bidimensional, em relação à sua representação gráfica, à correlação linear e à regressão linear. No estudo participaram 50 estudantes que se encontravam a frequentar o 2.º ano da Licenciatura em Educação Básica numa universidade do norte de Portugal. Os dados recolhidos dos estudantes foram obtidos através da aplicação de várias questões de probabilidades e estatística em ambiente formal de avaliação, das quais iremos aqui tratar apenas aquela que diz respeito à distribuição bidimensional. Finalmente, em termos de resultados, verificou-se que os estudantes foram mais sucedidos na representação gráfica da distribuição. Na avaliação do sinal e da intensidade da correlação linear, cerca de metade ou mais estudantes responderam corretamente. Finalmente, tiveram muitas dificuldades na regressão linear, aquando da determinação da estimativa do valor de uma das variáveis conhecido o valor da outra.
Palavras-chave: Distribuição bidimensional; Correlação linear; Regressão linear; Futuros professores dos primeiros anos
ABSTRACT
The aim of this paper is to analyse the statistics knowledge of a sample of prospective primary school teachers when they solve a task involving a two-dimensional distribution, in relation to the graphic representation, to the linear correlation and to the linear regression. The study involved 50 students, who were attending the 2nd year of the Bachelor in Basic Education at a university in the north of Portugal. The data were collected from the students’ answers through the application of several probability and statistics questions in a formal evaluation environment, of which we will deal here only with that concerning the two-dimensional distribution. Finally, in terms of results, the students were more successful in the graphic representation of the distribution. About half or more students were evaluated correctly in the signal and the intensity of the linear correlation. Finally, the students had many difficulties in the linear regression, when determining the estimation of the value for a variable known the value of the other.
Keywords: Two-dimensional distribution; Linear correlation; Linear regression; Prospective primary school teachers
RESUMEN
El objetivo de este trabajo es analizar el conocimiento estadístico de una muestra de futuros profesores de educación primaria cuando resuelven una tarea sobre la distribución bidimensional, en relación a su representación gráfica, a la correlación lineal y a la regresión lineal. En el estudio participaron 50 estudiantes, que se encontraban en el 2.º año de la Licenciatura en Educación Básica en una universidad del norte de Portugal. Los datos recogidos se obtienen de las respuestas de los estudiantes a varias cuestiones referidas a la probabilidad y la estadística en un ambiente formal de evaluación. En este trabajo tratamos solo las tareas referidas a la distribución bidimensional. En términos de resultados, los estudiantes obtuvieron mayor éxito en la representación gráfica de la distribución, mientras que en la evaluación del signo y de la intensidad de la correlación lineal cerca de la mitad o más de los estudiantes respondieron correctamente a la tarea. Finalmente, tuvieron muchas dificultades en cuanto a la regresión lineal, en torno a la estimación de un valor en una de las variables conocido el valor de la otra.
Palabras-clave: Distribución bidimensional; Correlación lineal; Regresión lineal; Futuros profesores de educación primaria
Introdução
A crescente utilização da estatística nos mais variados setores da sociedade e na vida quotidiana das pessoas tem-se repercutido no aprofundamento do seu ensino nas escolas. Atualmente, em Portugal, as probabilidades e estatística fazem parte dos programas de todos os anos escolares, tanto do ensino básico como do ensino secundário1 (Ministério da Educação e Ciência, 2013, 2014). No caso particular do ensino básico, as probabilidades e estatística incluem-se no domínio ‘Organização e Tratamento de Dados’, no qual os conteúdos estatísticos são aprofundados com o progresso dos ciclos e os conteúdos probabilísticos têm início apenas no 3.º ciclo. Assim, a inclusão do estudo do tema ‘Organização e Tratamento de Dados’ nos programas escolares requer que os professores adquiram uma formação que lhes permita implementar um ensino de probabilidades e estatística adequado às exigências do sistema de ensino e às necessidades dos alunos. Segundo Batanero (2009), nem sempre a componente de formação para ensinar estatística faz parte dos programas de formação inicial dos professores, especialmente na vertente didática, e esta questão é ainda mais problemática na medida em que só muito recentemente esses conteúdos (em particular, de probabilidades e estatística) foram incluídos nos programas escolares dos primeiros anos.
O conhecimento sobre a associação estatística e o estabelecimento de relações entre variáveis estatísticas reveste-se, atualmente, de uma importância fundamental, seja a nível do raciocínio científico, seja a nível da literacia científica, como salientam Bryant e Nunes (2012). Neste âmbito, as relações estatísticas, que traduzem situações de incerteza, perspetivam-se como complementares das relações funcionais, que traduzem situações deterministas.
Para Bryant e Nunes (2012), a aprendizagem de probabilidades é uma tarefa difícil que requer exigências cognitivas variadas, nomeadamente: compreender a natureza e as consequências da aleatoriedade; construir e categorizar o espaço amostral; comparar e quantificar probabilidades e raciocinar acerca de correlações. Além disso, no domínio ‘Organização e Tratamento de Dados’, do 3.º ciclo do ensino básico em Portugal, os professores devem preparar os alunos para “Utilizar tabelas de dupla entrada e diagramas em árvore na resolução de problemas envolvendo a noção de probabilidade e a comparação das probabilidades de diferentes acontecimentos compostos”(Ministério da Educação e Ciência, 2013, p. 83). Assim, embora estes futuros professores dos primeiros anos não tenham de ensinar a associação estatística aos seus alunos, o seu estudo justifica-se na medida em que ela é uma das exigências cognitivas da aprendizagem de probabilidades, além de que este conhecimento deve ser visto como conhecimento do conteúdo avançado, na perspetiva de Hill, Ball, e Schilling (2008).
No caso dos futuros professores dos primeiros anos escolares que participaram no presente estudo, eles cursam na universidade a unidade curricular semestral de Probabilidades e Estatística durante a sua formação inicial, o que não é muito diferente do que acontece em outras instituições portuguesas de formação destes professores. Esta unidade curricular está focada no conhecimento de conteúdos de probabilidades e estatística, e não se exploram nela aspetos didáticos. Em consonância, no âmbito da formação dos futuros professores dos primeiros anos, no presente estudo analisam-se os conhecimentos estatísticos destes futuros professores no tema distribuições bidimensionais, mais concretamente sobre a representação gráfica da distribuição, o sentido e a intensidade da correlação linear, e a previsão do valor de uma variável através da regressão linear.
Nas próximas secções apresentamos o enquadramento teórico, onde se reveem alguns estudos relacionados com a problemática da pesquisa; o método de investigação, em que explicitaremos o tipo de estudo, os participantes, a análise da tarefa proposta aos estudantes e os métodos de recolha e análise de dados; a apresentação e discussão de resultados segundo os conteúdos representação gráfica da distribuição, correlação linear e regressão linear; e, finalmente, sintetizam-se as conclusões e implicações do estudo.
1. Fundamentação teórica
A investigação sobre o conhecimento do professor para ensinar matemática é variada e oferece diferentes modelos teóricos que caracterizam os domínios ou componentes em que se estrutura o dito conhecimento (Godino, Giacomone, Batanero, & Font, 2017; Hill et al., 2008; Shulman, 1986). Em todos esses modelos identificam-se dois tipos de conhecimento fundamentais para o ensino: o conhecimento do conteúdo e o conhecimento pedagógico do conteúdo. No nosso estudo baseamo-nos no enquadramento teórico do Enfoque Ontossemiótico do conhecimento e instrução matemática (Godino, 2017; Godino, Batanero, & Font, 2007), pois os princípios em que se fundamenta respondem à nossa problemática e oferece-nos diferentes ferramentas, concetuais e metodológicas, para analisar o conhecimento a partir das resoluções de uma tarefa pelos futuros professores.
No Enfoque Ontossemiótico assume-se que o conhecimento matemático emerge das práticas (operativas e discursivas) que o sujeito realiza ao resolver uma amostra representativa de situações-problema relativas a um conteúdo matemático. Nesta prática matemática de resolução de problemas intervém uma diversidade de objetos matemáticos, como seja a linguagem (elementos referidos a termos, expressões, notações, gráficos, etc.), conceitos (que intervêm na resolução da tarefa e que se podem definir), propriedades (que podem apresentar-se como enunciados ou proposições e que regulam as práticas na resolução da tarefa), a diversidade de procedimentos que se podem empregar (operações, algoritmos, técnicas de cálculo), assim como o tipo de argumentação usada para provar ou justificar as práticas realizadas (Godino, 2002). Da interação entre os objetos matemáticos implicados numa tarefa (linguagem, conceitos, propriedades, procedimentos e argumentos) formam-se configurações, que podem ser de tipo epistémico (se são próprias de uma instituição) ou cognitivo (se são específicas do estudante – no nosso caso, futuros professores). O nosso interesse radica em analisar esta dualidade do conhecimento matemático, institucional versus pessoal, a partir das respostas dadas pelos futuros professores à tarefa envolvendo uma distribuição bidimensional. Logo, consideramos o significado de um ponto de vista institucional (no nosso caso, a educação secundária, porque é o nível escolar em que o conteúdo é abordado) ou de um ponto de vista pessoal (no nosso caso, os futuros professores dos primeiros anos escolares que estão a enfrentar a tarefa proposta) (Godino & Batanero, 1994). Para isso, usamos a proposta de análise dos objetos matemáticos realizada por Gea (2014), que oferece uma caracterização do significado institucional de referência da estatística bidimensional segundo a análise histórico-epistemológica do tema; a análise curricular; e refina as análises anteriores com o estudo detalhado da apresentação do tema numa ampla amostra de livros escolares do ensino secundário.
Nesse processo de comparação, a verificação de discrepâncias entre os significados institucional e pessoal conduz à identificação de conflitos semióticos, entendidos como uma “disparidade ou discordância entre os significados atribuídos a uma expressão por dois sujeitos (pessoas ou instituições) em interação comunicativa e [que] podem explicar as dificuldades e limitações das aprendizagens e do ensino implementado”(Godino, 2002, p. 250).
No mesmo sentido se considera o modelo de conhecimento proposto por Gea, Batanero, e Roa (2014) para que os estudantes adquiram uma aprendizagem significativa do tema, pois trata-se de orientações fundamentais na investigação didática sobre estes conteúdos, em que se descrevem os conhecimentos básicos a considerar no seu ensino (dados e distribuição, representação tabelar e gráfica, variabilidade, dependência, covariância e correlação, regressão e modelos de regressão), as atitudes e crenças favoráveis ao seu uso, o nível de pensamento e o raciocínio implicado nas tarefas sobre dados bivariados.
2. Antecedentes
A análise da associação das variáveis estatísticas de um estudo é definida por diversos autores como uma atividade cognitiva fundamental (McKenzie & Mikkelsen, 2007; Moritz, 2004; Zieffler, 2006), que realizamos habitualmente na nossa vida quotidiana e que nos ajuda a tomar decisões fundamentadas a partir de dados (Estepa, Gea, Cañadas, & Contreras, 2012).
No estudo de dados bivariados responde-se a duas problemáticas fundamentais: por um lado, analisa-se a relação entre duas variáveis, onde interessa avaliar a intensidade da dependência entre essas variáveis (análise da correlação), e, por outro lado, no caso de a dependência ser significativa, interessa estabelecer um modelo de ajuste entre as variáveis analisadas, que permita estimar o valor de uma das variáveis conhecido o valor da outra (análise da regressão). A estes campos de problemas, Gea (2014) acrescenta um campo de problemas inicial, relativo à organização e representação dos dados bivariados em tabelas e gráficos, com que se confrontam os estudantes no início do estudo do tema. No nosso estudo foi proposto aos estudantes resolverem uma tarefa em que se encontram implicados estes três tipos de problemas.
Apesar da utilidade do tema e de tratar-se de um conteúdo matemático incluído nos programas escolares do ensino secundário da maioria dos países (Common Core State Standards Initiative, 2010; Ministério da Educação e Ciência, 2014; Ministerio de Educación, Cultura y Deporte, 2015), a investigação em educação matemática informa-nos dos enviesamentos e conceções erradas que os estudantes revelam, que inclusive persistem depois do ensino (Estepa, 2004). Concretamente, destacamos a dificuldade em explicar o tipo de dependência que as variáveis apresentam, uma vez que nem sempre ela é devida a uma relação de causa e efeito, sendo possível que se deva à influência de outras variáveis ou que se trate de uma dependência casual, entre outras descritas por Barbancho (1973).
Em investigações como a realizada por Estepa (2007), observa-se que os alunos do ensino secundário manifestam um conhecimento adequado sobre o facto de o coeficiente de correlação ser adimensional (mais de 85% de alunos reconhecem esta propriedade), mas revelam dificuldades em reconhecer se duas variáveis conformam uma distribuição bidimensional (só metade dos estudantes determinam corretamente a distribuição bidimensional), em estimar a correlação quando comparam valores do coeficiente de correlação distintos de -1, 0 e 1, assim como em diferenciar a variável dependente da independente no modelo de regressão linear. Também num estudo conduzido por Mugabe, Fernandes, e Correia (2012), a partir da apresentação de uma distribuição bidimensional através de um diagrama de dispersão, questionaram-se futuros professores moçambicanos do ensino secundário sobre a existência de associação entre as variáveis e a previsão do valor de uma das variáveis. Em termos de resultados verificou-se que os estudantes revelaram muitas dificuldades, como sejam usar teorias prévias ou analisar a dependência entre duas variáveis a partir de dados isolados, mesmo depois do ensino da associação estatística e da regressão linear.
Finalmente, destacamos o trabalho de Quintas, Ferreira, e Oliveira (2015), que observam o ensino de duas professoras do ensino secundário, com ampla experiência, quando explicam aos alunos o tema de estatística bidimensional. Nos seus resultados, os autores descobriram que as professoras revelam falta de conhecimento estatístico sobre propriedades como a existência de duas linhas de regressão, ou extrapolam para um intervalo de valores muito mais amplo do que aquele que corresponde aos dados, sem reconhecer as implicações no erro da estimativa.
3. Método de investigação
No presente artigo analisam-se os conhecimentos estatísticos que os estudantes, futuros professores dos primeiros anos, aplicaram no estudo de uma distribuição estatística bidimensional, no que respeita à representação gráfica da distribuição, à correlação linear e à regressão linear.
Participaram no estudo 50 estudantes (designados por Ei, com i = 1, 2, …, 50) de uma universidade portuguesa, que se encontravam a frequentar a unidade curricular de Probabilidades e Estatística, integrada no 2.º ano do curso de Licenciatura em Educação Básica. À entrada na universidade, estes estudantes tinham uma formação matemática muito variada, o que explica as perceções diversas sobre as suas dificuldades nas disciplinas de matemática que tinham frequentado na universidade, com 28% a declararem ter muita dificuldade, 44% a declararem ter dificuldade, 24% a declararem ter pouca dificuldade e 4% a declararem não ter dificuldade, de acordo com o questionário sobre formação prévia em matemática realizado em sala de aula. Assim, conclui-se que quase três em cada quatro estudantes afirmaram ter dificuldade ou muita dificuldade nas disciplinas de matemática entretanto frequentadas na universidade.
A recolha de dados foi efetuada através da aplicação de várias tarefas em sala de aula, em contexto de avaliação formal e depois de concluída a lecionação da unidade curricular de Probabilidades e Estatística. Dessas tarefas, estudamos aqui apenas uma, que se apresenta na Figura 1. Na altura em que os futuros professores resolveram a tarefa proposta, eles já tinham estudado o tema de estatística bidimensional no âmbito da unidade curricular antes referida, tendo esse tema sido estudado numa perspetiva de conteúdo matemático, abordando fundamentalmente os conteúdos delimitados pelo currículo do ensino secundário (Ministério da Educação e Ciência, 2014). Assim, nesse tema, foram exploradas, numa vertente intuitiva e com apoio de tecnologia, a representação gráfica de distribuições bidimensionais através do diagrama de dispersão, a correlação linear e a regressão linear.
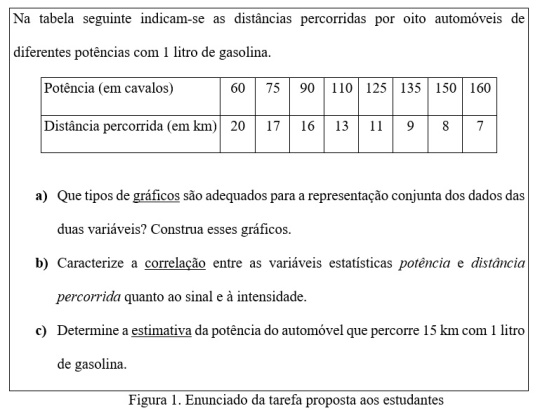
Em cada item da tarefa requer-se que o estudante comece por decidir quais os tipos de análises estatísticas adequadas em termos de representação gráfica da distribuição bidimensional dada (no item a), de caracterização da correlação linear entre as duas variáveis quanto ao sentido e à intensidade (no item b) e de previsão do valor de uma das variáveis conhecido o valor da outra variável (no item c).
No item 1, esperava-se que os estudantes construíssem o diagrama de dispersão ou nuvem de pontos dos dados bidimensionais da tarefa, como se mostra na Figura 2. Em Gea, Batanero, Fernandes, e Gómez (2014) descrevem-se os tipos de representações gráficas que podemos utilizar na análise da correlação e regressão, mas no nosso estudo os dados têm frequência 1, logo não é útil outro tipo de representação tridimensional (diagrama de barras, diagrama de bolhas, etc.).
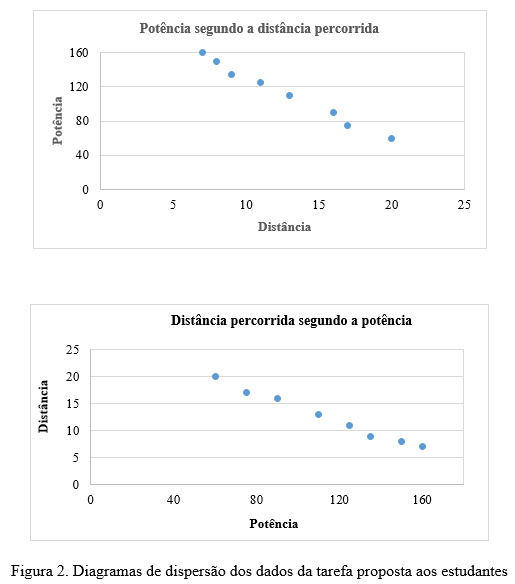
No item 2, esperava-se que os estudantes caracterizassem a correlação linear entre as duas variáveis quanto ao sentido e à intensidade mediante o uso de operações simbólicas, através da fórmula de cálculo do coeficiente de correlação linear ou recorrendo a um procedimento discursivo envolvendo argumentos sobre as propriedades da correlação linear. No primeiro caso, pode-se utilizar a disposição tabelar dos dados da tarefa, pois é fácil obter a covariância entre as variáveis quando os dados têm frequência 1. No segundo caso, a disposição tabelar das variáveis permite-nos deduzir que a correlação tem sentido negativo, dado que na tabela se observa que os dados da variável potência estão ordenados de forma crescente e corresponde a um ordenamento decrescente da variável dependente. Por último, ao aplicar a fórmula do coeficiente de correlação linear, obtemos o valor -0,995, o qual é elevado e negativo.
No item 3, esperava-se que os estudantes previssem o valor de uma das variáveis (potência do automóvel) conhecido o valor da outra variável (15 km que percorre o automóvel com 1 litro de gasolina), mediante a interpolação e recorrendo a uma função de ajuste linear aos dados da tarefa. A função pode ser obtida de maneira aproximada (estimada “a olho”) a partir da representação gráfica dos dados bidimensionais do item a). De maneira mais precisa, pode-se calcular a reta da potência de um automóvel (y), conhecida a distância percorrida com 1 litro de gasolina (x), segundo os parâmetros da reta de regressão dos mínimos quadrados, que é dada pela expressão: y = -7,6x + 209,2, sendo o valor estimado, aproximadamente, de 95 cavalos de potência.
À semelhança do que aconteceu nas aulas da disciplina de Probabilidades e Estatística, na resolução da tarefa os estudantes puderam utilizar uma folha de cálculo ou uma calculadora gráfica. Ora, o facto de estas tecnologias permitirem construir o diagrama de dispersão, determinar o valor do coeficiente de correlação linear de Pearson e definir a reta de regressão mostra o seu potencial contributo para a resolução dos itens da tarefa.Finalmente, em termos de organização e análise de dados, começa-se por apresentar as estratégias escolhidas pelos estudantes para a análise dos dados fornecidos no enunciado da tarefa, em cada um dos três itens, e determinam-se as frequências de estudantes que escolheram cada uma delas, resumindo-se toda essa informação em tabelas. De seguida, estuda-se a correta aplicação dos procedimentos escolhidos pelos estudantes, indicam-se também os tipos de conflitos semióticos revelados nas suas respostas e apresentam-se, a título de exemplo, algumas respostas dos estudantes. Para fundamentar a discussão dos resultados, consideramos o significado institucional de referência (ao nível do ensino secundário) proposto por Gea (2014), o qual é baseado no enquadramento teórico do Enfoque Ontossemiótico.
4. Apresentação de resultados
Nesta secção apresentam-se e discutem-se os resultados obtidos segundo os conteúdos contemplados em cada um dos itens da tarefa: a) representação gráfica da distribuição; b) caracterização da correlação linear entre as duas variáveis quanto ao sentido e à intensidade; e c) estudo da regressão linear para efetuar a previsão do valor de uma das variáveis conhecido o valor da outra variável.
4.1. Representação gráfica da distribuição
No caso das distribuições bidimensionais, o diagrama de dispersão ou nuvem de pontos é uma representação gráfica adequada, sendo apenas essa a representação gráfica que os estudantes tinham estudado na unidade curricular de Probabilidades e Estatística. A seguir, na Tabela 1, apresentam-se as representações gráficas referidas pelos estudantes como sendo adequadas para representar a distribuição.

Pela Tabela 1 verifica-se que quase todos os estudantes consideraram que seria adequado recorrer ao diagrama de dispersão para representar a distribuição bidimensional. Destes estudantes, sete ajustaram ainda, de forma aproximada, a reta de regressão à nuvem de pontos. Ainda assim, além dos que não responderam a este item, verificou-se que cerca de um em cada quatro estudantes indicaram um gráfico não adequado para representar os dados, designadamente um gráfico de barras, um histograma ou um gráfico de linhas, os quais são adequados para representar distribuições unidimensionais.
Na construção do diagrama de dispersão (dois estudantes selecionaram este gráfico, mas não o construíram), 27 estudantes definiram pontos de coordenadas (potência, distância), enquanto 12 estudantes definiram pontos de coordenadas (distância, potência), o que significa que entre os diagramas de dispersão se trocaram as variáveis independente e dependente. Também no caso dos gráficos de barras (dois estudantes indicaram este tipo de gráfico, mas não o construíram), cinco estudantes consideraram a potência no eixo horizontal e três estudantes consideraram-na no eixo vertical, denotando novamente a troca entre as variáveis independente e dependente.
Apesar da elevada percentagem de estudantes que selecionaram o tipo de representação gráfica adequada para representar os dados, verificou-se que seis estudantes não construíram os gráficos, como era pedido, cinco uniram os pontos do diagrama de dispersão por segmentos de reta, 32 não escreveram o título do gráfico, oito não nomearam o eixo horizontal, nove não nomearam o eixo vertical e dois não definiram as escalas nos eixos. As reduzidas dificuldades reveladas pelos estudantes no estabelecimento das escalas nos eixos compreendem-se pelo facto de eles terem usado uma folha de cálculo ou uma calculadora gráfica na construção do gráfico de dispersão na unidade curricular de Probabilidades e Estatística, e também na presente tarefa.
Constatou-se, ainda, que quatro estudantes chamam gráfico de pontos ao diagrama de dispersão, dois chamam gráfico de linhas ao diagrama de dispersão (depois de terem unido os pontos por segmentos de reta) e um chama histograma ao gráfico de barras. Nas Figuras 3 e 4 podem-se observar as representações gráficas escolhidas e contruídas por dois estudantes.
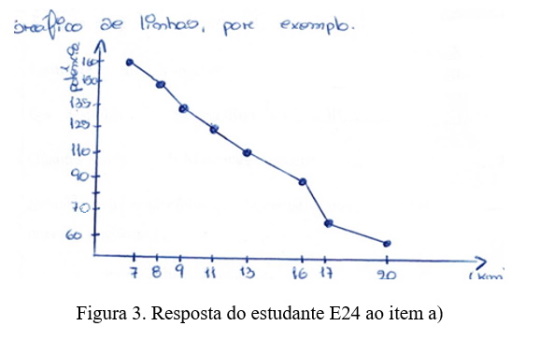
Na Figura 3 verifica-se que o estudante E24 alterou a ordem com que eram apresentadas as variáveis potência e distância no enunciado, o que poderia dever-se à necessidade de considerar a distância como variável independente na equação da reta de regressão do item c). Todavia, isso não aconteceu, pois o estudante não recorreu à reta de regressão. Adicionalmente, o estudante uniu os pontos do diagrama de dispersão por segmentos de reta, o que explica a sua designação de gráfico de linhas, manifestando um conflito semiótico ao usar uma linguagem relativa à distribuição unidimensional. Podemos detetar a disparidade de significado que o estudante revela quanto à distribuição de dados bidimensionais, pois os dados referem-se a sujeitos do estudo e não a valores de uma variável unidimensional e suas respetivas frequências (eixo vertical), e o estudante aplica este gráfico por encontrar dados bidimensionais nos eixos coordenados. Finalmente, o estudante não definiu o título do gráfico, não assinalou a origem do sistema de eixos, nem definiu corretamente as escalas nos eixos.
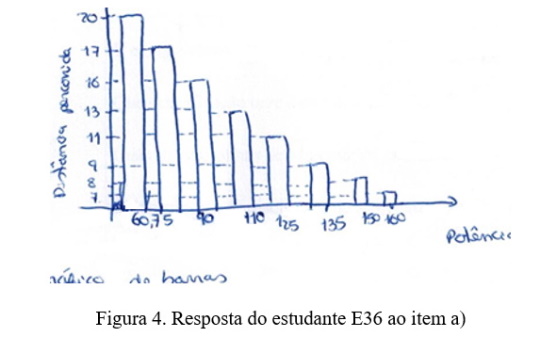
Observando a Figura 4, verifica-se que o estudante E36 construiu o gráfico de barras considerando os valores da variável potência como categorias (variável independente) e os valores da variável distância como as correspondentes frequências absolutas, o qual não é um gráfico adequado para o estudo de distribuições bidimensionais. Como no caso que se mostrou na Figura 3, o estudante manifesta o conflito semiótico relativo à linguagem envolvida no estudo da distribuição unidimensional, ao considerar os valores da variável dependente (distância percorrida) como frequências absolutas (eixo vertical) da variável independente (potência). Também este gráfico, tal como o gráfico anterior, não tem título, não se referencia a origem do sistema de eixos nem se definiram corretamente as escalas nos eixos.
4.2. Correlação linear
No item b) pedia-se que os estudantes caracterizassem a distribuição bidimensional quanto ao sinal (positiva ou negativa) e quanto à intensidade (forte, média ou fraca) da dependência das variáveis que a compõem (potência e distância). Tendo os estudantes, na unidade curricular de Probabilidades e Estatística, estudado a caracterização da correlação linear a partir da análise intuitiva do diagrama de dispersão e da determinação do coeficiente de correlação de Pearson, obtido através da utilização de uma folha de cálculo ou da calculadora gráfica, esperava-se que os estudantes concluíssem que se tratava de uma correlação linear negativa e forte. Na Tabela 2 apresentam-se as frequências de estudantes segundo os diferentes tipos de resposta para caracterizar a correlação linear, tendo em conta que alguns estudantes avaliaram apenas um dos atributos: o sinal ou a intensidade. Assim, 10 estudantes avaliaram apenas o sentido da correlação, três avaliaram apenas a intensidade da correlação e 28 avaliaram o sentido e a intensidade da correlação.
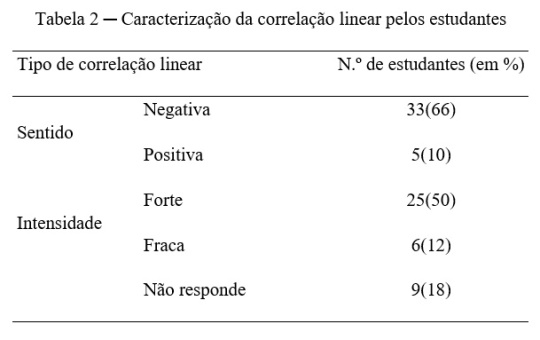
Pela Tabela 2 conclui-se que metade (ou mais) dos estudantes afirmaram que a correlação linear é negativa e forte, que é a resposta que caracteriza adequadamente a distribuição dada quanto aos atributos sinal e intensidade. Estes resultados agravam-se consideravelmente na medida em que muitos estudantes não apresentaram qualquer justificação para as suas avaliações da correlação. Independentemente de a resposta ser correta ou incorreta, não apresentaram qualquer justificação para o sentido da correlação sete estudantes, para a intensidade da correlação quatro estudantes e para ambos os atributos 18 estudantes.
Quando os estudantes justificaram as suas avaliações acerca de pelo menos um dos atributos (sinal e intensidade) da correlação linear, verificou-se que adotaram duas estratégias: uma estratégia intuitiva baseada na análise do diagrama de dispersão (13 estudantes), que tinha sido construído no item anterior; e outra estratégia baseada na análise do valor do coeficiente de correlação de Pearson (três estudantes). Na Figura 5 apresenta-se a resposta de um estudante que recorreu a uma análise intuitiva a partir da observação do diagrama de dispersão.

Já na segunda estratégia, os estudantes usaram uma folha de cálculo ou uma calculadora gráfica para determinarem o valor do coeficiente de correlação de Pearson e avaliaram a localização desse valor no intervalo [-1, 1], como se mostra na resposta da Figura 6.

Finalmente, para além dos não respondentes, verificou-se que cinco estudantes afirmaram tratar-se de uma correlação positiva e seis referiram tratar-se de uma correlação fraca, o que, ao todo, representa 22% do universo. Estes estudantes revelaram conflitos semióticos ligados às propriedades da covariância e da correlação, como se exemplifica na resposta da Figura 7. Nestes casos, os estudantes não observam que os dados bidimensionais no diagrama de dispersão informam do seu ajuste a uma curva reconhecível como é a linear, com elevada intensidade (devido à dispersão dos dados no diagrama) e com um declive negativo, o que informa do sentido e da intensidade da correlação.
Além disso, no estudo, nenhum estudante recorreu à propriedade da covariância e à correlação ligada à divisão do diagrama de dispersão em quatro quadrantes através das médias marginais de cada variável (a saber, pelas linhas perpendiculares referidas às médias de cada variável unidimensional), pois os dados na tarefa concentram-se no segundo e quarto quadrantes.

A resposta do estudante E14, alicerçada na observação do diagrama de dispersão, refere-se apenas ao sentido da correlação, embora a sua justificação pareça estar mais relacionada com a intensidade da correlação, pois, em geral, a dispersão é avaliada em relação à reta que melhor se ajusta aos dados.
4.3. Regressão linear
Por último, no item c) pretendia-se determinar uma estimativa do valor de umas das variáveis a partir do conhecimento do valor da outra variável, – neste caso, uma estimativa da potência de um automóvel que percorre 15 km com 1 litro de gasolina. Para tal, os estudantes deviam definir a reta de regressão linear, do tipo y=ax+b, em que x se refere à variável independente (distância) e y se refere à variável dependente (potência). Uma vez conhecida a equação de regressão linear, determinada através de uma folha de cálculo ou de uma calculadora gráfica, basta substituir o valor da distância na equação para obter a estimativa do valor da potência. Na Tabela 3 estão registadas as diferentes estratégias usadas e as frequências de estudantes que as adotaram.

Dos três itens da tarefa, o item c) foi aquele em que se verificou o maior número de não respostas: especificamente, 30% dos estudantes não responderam. Com percentagens semelhantes de estudantes, salienta-se o recurso à regra de três simples e a seleção de um valor da potência compreendido entre 90 e 110 cavalos, métodos que não garantem a obtenção de uma estimativa adequada e que envolvem uma grande subjetividade.
No caso da regra de três simples, tal significaria que a relação entre as variáveis estatísticas seria uma relação funcional de proporcionalidade direta, o que, em geral, não se verifica nas relações estatísticas. Isso ficou bem patente quando os estudantes tomaram diferentes pares de valores da distribuição dada para estabelecerem a regra de três simples, o que conduziu a resultados também diversos. Na Figura 8 apresenta-se um exemplo de resposta obtida recorrendo a esta estratégia.

Repare-se que a consideração de qualquer outro par de valores na regra de três simples conduz a um valor diferente da potência. Por exemplo, o estudante E5 considerou o par (13 km, 110 cavalos) e obteve a potência de 126 cavalos.
No caso da seleção de um valor compreendido entre 90 e 110 cavalos, os estudantes consideraram que esse valor seria uma estimativa adequada pois a distância percorrida está compreendida entre 13 km e 16 km, portanto contém o valor dado (15 km). Na Figura 9 apresenta-se um exemplo desta estratégia.

Na resposta do estudante E25 observa-se que ele excluiu da sua análise o valor mais extremo (17 km), considerando dois valores para estimativa da potência: 95 ou 100 (cavalos). Estes valores estão compreendidos entre 90 e 110 (cavalos), aos quais correspondem, por sua vez, distâncias compreendidas entre 13 km e 16 km, intervalo em que situa o valor dado de 15 km. Na determinação da reta de regressão, que os estudantes puderam obter através da utilização de uma folha de cálculo ou da calculadora gráfica, é necessário fixar para variável independente a variável cujo valor é conhecido (neste caso, a distância) e para variável dependente a variável cuja estimativa pretendemos determinar (neste caso, a potência). Assim, os três estudantes que consideraram a relação (potência, distância), isto é, a potência como variável independente e a distância como variável dependente, obtiveram uma estimativa errada para a potência. Já os três estudantes que consideraram a relação (distância, potência) obtiveram uma estimativa correta para a potência. A seguir, nas Figuras 10 e 11, apresenta-se um exemplo de cada uma destas estratégias.

O estudante E44, erradamente, considerou a potência para variável independente e a distância para variável dependente, quando devia trocar os papéis dessas variáveis para obter a equação de regressão linear que permite estimar um valor da potência conhecido o valor da distância.

Já o estudante E39 considerou corretamente a distância como variável independente e a potência como variável dependente, o que conduziu à obtenção da equação correta de regressão e, portanto, à adequada estimativa do valor da potência. Pode reparar-se que as estimativas da potência por qualquer das duas retas de regressão linear são muito próximas, o que se explica pelo facto de estarmos face a uma correlação muito forte, quase perfeita (r = - 0.995).
Finalmente, o estudante que recorre ao conceito de média começa por calcular a média das potências dadas e, de seguida, determina uma nova potência para que a média venha aumentada de uma unidade. Naturalmente que este raciocínio não tem ligação com o que é pedido e conduziu a uma resposta errada.
5. Discussão e conclusões
No presente estudo indaga-se o conhecimento de estatística bidimensional que os futuros professores dos primeiros anos aplicaram na resolução de uma tarefa no que respeita a representar a distribuição, avaliar o sentido e a intensidade da correlação linear e determinar a estimativa do valor de uma variável através da regressão linear. Os resultados mostram os diferentes conflitos semióticos que os participantes do nosso estudo manifestaram, os quais também foram observados em outros estudos (e.g., Estepa, 2007; Quintas et al., 2015). No presente estudo, esses conflitos ligam-se, principalmente, com a linguagem e propriedades relativas ao tema.
Quanto à linguagem, encontrámos futuros professores com uma limitada competência na construção de gráficos estatísticos, uma vez que descuidam as escalas dos eixos, o título do gráfico e dos eixos, etc., que são objetos requeridos na construção e leitura crítica de tabelas e gráficos estatísticos (Arteaga, Batanero, Cañadas, & Contreras, 2011; Fernandes, Batanero, & Gea, 2019). Além disso, não distinguem o significado de cada tipo de gráfico estatístico (de linhas, barras, dispersão, etc.) a partir da informação dada na tarefa. Dificuldades análogas foram também observadas por Fernandes, Morais, e Lacaz (2011) em alunos do 9.º ano.
Quanto às propriedades relativas ao tema, os principais conflitos radicam na interpretação da dispersão dos dados bidimensionais através da nuvem de pontos, segundo a caracterização da correlação linear entre as duas variáveis quanto ao sentido e à intensidade, o que implica que alguns participantes atribuam uma correlação positiva e débil à informação representada no gráfico. Também se observa que alguns estudantes não prestam atenção aos distintos papéis que desempenham as variáveis na análise da regressão. É importante detetar este tipo de conflitos no ensino e aprendizagem do tema porque o estudo da correlação é o passo prévio à determinação de uma função de ajuste entre as variáveis, assim como distinguir entre a variável dependente e independente para poder estimar o valor de uma variável em função do valor da outra através da reta de regressão.
Os resultados obtidos comprometem-nos a continuar avançando nesta linha de pesquisa, onde esperamos obter um melhor desempenho dos futuros professores dos primeiros anos em torno da estatística bidimensional. A relevância resulta não só da importância de o futuro professor ter formação adequada para o seu desenvolvimento e desempenho profissional, mas também de a literatura prévia recomendar o ensino de estudos bidimensionais no ensino primário, pelo que os professores devem estar bem preparados para os desafios que surgirão no seu futuro profissional. Em particular, como recomendado por Moritz (2004), é importante introduzir o estudo de estatística bivariada no ensino básico através da análise de gráficos e tabelas de séries temporais, onde a associação pode ser considerada de forma natural. Ao contemplar a variação da variável de interesse em termos de tempo, essa abordagem da variação temporal permite ao aluno focar-se na mudança de uma variável através da variação implícita da variável tempo.
Por fim, consideramos que este trabalho também é útil para o formador de professores pois informa do conhecimento que têm os estudantes, futuros professores, no estudo de uma distribuição bidimensional.
Referências
Arteaga, P., Batanero, C., Cañadas, G., & Contreras, J. M. (2011). Las tablas y gráficos estadísticos como objetos culturales. Números, 76, 55-67. [ Links ]
Barbancho, A. G. (1973). Estadística elemental moderna. Barcelona, España: Ariel. [ Links ]
Batanero, C. (2009). Retos para la formación estadística de los profesores. In J. A. Fernandes, M. H. Martinho, F. Viseu, & P. F. Correia (Orgs.), Actas do II Encontro de Probabilidades e Estatística na Escola (pp. 52-71). Braga, Portugal: Centro de Investigação em Educação da Universidade do Minho. [ Links ]
Batanero, C., Burrill, G., & Reading, C. (2011). Teaching statistics in school mathematics challenges for teaching and teacher education: A Joint ICMI/IASE study. New York: Springer. [ Links ]
Bryant, P., & Nunes, T. (2012). Children´s understanding of probability: A literature review (full report). London, UK: The Nuffield Foundation. [ Links ]
Common Core State Standards Initiative. (2010). Standards for mathematical practice. Recuperado de http://www.corestandards.org/ [ Links ]
Estepa, A. (2004). Investigación en educación estadística. La asociación estadística. In R. Luengo (Ed.), Líneas de investigación en Educación Matemática (pp. 227-255). Badajoz, España: Servicio de Publicaciones da Universidad de Extremadura. [ Links ]
Estepa, A. (2007). Caracterización del significado de la correlación y regresión de estudiantes de Educación Secundaria. Zetetiké, 15(28), 119-151. [ Links ]
Estepa, A., Gea, M. M., Cañadas, G. R., & Contreras, J. M. (2012). Algunas notas históricas sobre la correlación y regresión y su uso en el aula. Números, 81, 5-14. [ Links ]
Fernandes, J. A., Batanero, C., & Gea, M. M. (2019). Escolha e aplicação de métodos estatísticos por futuros professores dos primeiros anos. In J. M. Contreras, M. M. Gea, M. M. López-Martín, & E. Molina- Portillo (Eds.), Actas del Tercer Congreso Internacional Virtual de Educación Estadística. Granada, España: Universidade de Granada. [ Links ]
Fernandes, J. A., Morais, P. C., & Lacaz, T. V. S. (2011). Representação de dados através de gráficos estatísticos por alunos do 9.º ano de escolaridade. In Anais da XIII Conferência Interamericana de Educação Matemática, Recife, Brasil, 26-30 junho. [ Links ]
Gea, M. M. (2014). La correlación y regresión en bachillerato: Análisis de libros de texto y del conocimiento de los futuros profesores (Tesis doctoral). Universidad de Granada, Granada, [ Links ] España.
Gea, M. M., Batanero, C., Cañadas, G. R., & Contreras, J. M. (2013). Un estudio empírico de las situaciones-problema de correlación y regresión en libros de texto de Bachillerato. In A. Berciano, G. Gutiérrez, A. Estepa, & N. Climent (Eds.), Investigación en Educación Matemática XVII (pp. 293-300). Bilbao, España: SEIEM. [ Links ]
Gea, M. M., Batanero, C., Fernandes, J. A., & Gómez, E. (2014). La distribución de datos bidimensionales en los libros de textos de matemáticas de Bachillerato. Quadrante, 23(2), 147-172. [ Links ]
Gea, M., Batanero, C., & Roa, R. (2014). El sentido de la correlación y regresión. Números, 87, 25-35. [ Links ]
Godino, J. D. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactique des Mathématiques, 22(2/3), 237-284. [ Links ]
Godino, J. D. (2017). Construyendo un sistema modular e inclusivo de herramientas teóricas para la educación matemática. In J. M. Contreras, P. Arteaga, G. R. Cañadas, M. M. Gea, B. Giacomone, & M. M. López-Martín (Eds.), Actas del Segundo Congreso International Virtual sobre el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos. Recuperado de http://enfoqueontosemiotico.ugr.es/civeos.html [ Links ]
Godino, J. D., & Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14(3), 325-355. [ Links ]
Godino, J. D., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. [ Links ]
Godino, J. D., Giacomone, B., Batanero, C., & Font, V. (2017). Enfoque ontosemiótico de los conocimientos y competencias del profesor de matemáticas. Bolema, 31(57), 90-113. [ Links ]
Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372-400.
McKenzie, C. R. M., & Mikkelsen, L. A. (2007). A Bayesian view of covariation assessment. Cognitive Psychology, 54(1), 33-61. [ Links ]
Ministério da Educação e Ciência (2014). Programa de Matemática A – Ensino secundário. Lisboa, Portugal: Ministério da Educação e Ciência. [ Links ]
Ministério da Educação e Ciência. (2013). Programa de Matemática para o ensino básico. Lisboa, Portugal: Ministério da Educação e Ciência. [ Links ]
Ministerio de Educación, Cultura y Deporte. (2015). Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato. Madrid: Ministerio de Educación, Cultura y Deporte. [ Links ]
Moritz, J. (2004). Reasoning about covariation. In D. Ben-Zvi & J. Garfield (Eds.), The challenge of developing statistical literacy, reasoning and thinking (pp. 221-255). Dordrecht, Netherlands: Kluwer. [ Links ]
Mugabe, A. D., Fernandes, J. A., & Correia, P. F. (2012). Avaliação da associação estatística num diagrama de dispersão por estudantes universitários. In H. Pinto, H. Jacinto, A. Henriques, A. Silvestre, & C. Nunes (Orgs.), Atas do XXIII Seminário de Investigação em Educação Matemática (pp. 403-414). Lisboa, Portugal: Associação de Professores de Matemática. [ Links ]
Quintas, S., Ferreira, A., & Oliveira, H. (2015). O conhecimento didático de estatística de duas professoras de matemática sobre dados bivariados. Bolema, 29(51), 284-306. [ Links ]
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 3-14. [ Links ]
Zieffler, A. S. (2006). A longitudinal investigation of the development of college students’ reasoning about bivariate data during an introductory statistics course (Tese de doutoramento). Universidade de Minnesota, Minnesota, EUA.
Toda a correspondência relativa a este artigo deve ser enviada para: José António Fernandes
Instituto de Educação, Universidade do Minho, Campus de Gualtar
4710-057 Braga, Portugal
E-mail: jfernandes@ie.uminho.pt
Recebido em 21 de dezembro de 2018
Aceite para publicação em 8 de dezembro de 2019
NOTAS
1Em Portugal, o ensino básico desenvolve-se ao longo dos primeiros nove anos de escolaridade e estrutura-se em três ciclos: 1.º ciclo, do 1.º ano ao 4.º ano; 2.º ciclo, 5.º e 6.º anos; e 3.º ciclo, do 7.º ano ao 9.º ano.