Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Análise Psicológica
Print version ISSN 0870-8231On-line version ISSN 1646-6020
Aná. Psicológica vol.37 no.3 Lisboa June 2019
https://doi.org/10.14417/ap.1576
Children’s understanding of the idea of logical necessity: The effect of counter-suggestions
A compreensão da ideia de necessidade lógica em crianças: O efeito das contra-sugestões
Orlando Lourenço1
1Faculdade de Psicologia, Universidade de Lisboa, Lisboa, Portugal
ABSTRACT
This study examined the child’s understanding of the idea of logical necessity in 40 preoperational and 40 operational children in the context of a number conservation task and a liquids conservation task. The first task followed the typical Piagetian clinical method. The second task also used this method, but it employed counter-suggestions that Piaget, in a surprising way, rarely, if ever, used in his experiments. Children’s performance on the number conservation task allowed us, in a pre-experimental phase, to classify those children, aged between 5 and 7 years, as preoperational (40) or operational (40). Results show that: (1) from the number conservation task to the liquids conversation task, there was a significant change in preoperational and operational children’s epistemic status and its corresponding idea of logical necessity; (2) children refused a non-justified counter-suggestion coming from a putative knowledgeable adult less than a justified contra-suggestion coming from a hypothetical child; (3) operational children often invoked the identity argument on both tasks and the reversibility argument was practically absent; (4) children invoked the compensation argument on the liquids conservation task more than on the number conservation task.
Key words: Piaget, Children, Counter-suggestions, Logical necessity, Operational arguments.
RESUMO
O problema da necessidade lógica ou conhecimento necessário é central na teoria de Piaget. Este estudo examinou essa necessidade no desempenho de 80 crianças na prova de conservação de líquidos. Estas crianças tinham sido avaliadas previamente como pré-operatórias (40) ou operatórias (40) com base no seu desempenho numa fase pré-experimental na prova do valor cardinal de um conjunto segundo o típico método clínico Piagetiano. Na fase experimental, recorremos a dois tipos de contra-sugestão estranhamente não usados por Piaget. Os principais resultados mostram que (1) nem todas as crianças pré-operatórias como operatórias tinham a mesma ideia de necessidade lógica, já que algumas mudaram o seu estatuto operatório ou epistémico da fase pré-experimental para a experimental; (2) as crianças recusaram menos uma contra-sugestão não justificada de um adulto perito na noção em jogo do que uma contra-sugestão justificada e provinda de uma criança hipotética da idade da criança entrevistada, sendo este dado mais visível nas crianças pré-operatórias do que operatórias; (3) o argumento operatório da identidade foi o mais invocado pelas crianças operatórias em ambas as provas e o argumento da reversibilidade nunca apareceu; e (4) o argumento da compensação foi mais invocado na prova da conservação de líquidos do que na prova do valor cardinal de um conjunto. Alguns destes resultados são consistentes com a teoria de Piaget, mas outros desafiam-na em extensão considerável.
Palavras-chave: Piaget, Conhecimento necessário, Método clínico, Contra-sugestões, Crianças pré-operatórias e operatórias, Argumentos operatórios.
The child’s understanding of the idea of logical necessity involved in necessary knowledge is a central issue in Piaget’s (1983, 1986, 1987a,b) theory (see also Beilin, 1992; Carpendale & Lewis, 2004; Lourenço, 2014, 2016; Lourenço & Machado, 1996; Müller, Carpendale, & Smith, 2009; Smith, 1996). Piaget (1978, p. 5; see also Chapman, 1988, p. 309) even said that this issue constitutes what he called the second great mystery of knowledge: How do new and qualitatively distinct forms of knowing that appear over development come to be understood not only as what is the case, true knowledge, but also as what has to be the case and could not be otherwise, necessary knowledge? Parenthetically, the first mystery of knowledge has to do with the appearance and evolving of such forms of knowing in the course of ontogenesis (see Inhelder & Piaget, 1958; Piaget, 1950a,b,c; Piaget & Inhelder, 1969a).
The child’s understanding that the number of elements in a set remains constant regardless of their spatial configuration in the set at hand is an example of logical necessity and necessary knowledge (Lourenço, 2014; Piaget, 1986, 1987a,b; Ricco, 1990; Smith, 1993, 1997, 2009). As Piaget (1967) recognized, the problem of logical necessity involved in necessary knowledge is “the central problem of the psychogenesis of logical structures” (p. 391). This explains Piaget’s concern with the child’s understanding of necessary knowledge and the idea of logic necessity throughout his research program (Piaget, 1918, 1986, 1987a,b, 2004).
Although systematically explored in the second half of 20th century (e.g., Miller, 1986; Miller, Brownell, & Zukier, 1977; Miller & Lipps, 1973), Piaget’s views on the child’s understanding of the idea of logical necessity are, with a few exceptions (Caroff, 2002; Lourenço, 2012, 2016; Miller, Custer, & Nassau, 2000; Müller et al., 2009; Overton, 1990; Smith, 2009) barely studied nowadays. Even so, we know of no study addressing children’s understanding of the idea of logical necessity (e.g., Miller, Brownell, & Zukier, 1977; Miller et al., 2000; Smith, 1993) that does not refer to Piaget’s views on necessary knowledge and logic necessity (Piaget, 1986, 1987a,b).
Piagetian questions were abandoned because of both the appearance of new fields of research (e.g., neurosciences, dynamic-systems approaches, evolutionary psychology), and the idea that Piaget became a figure of the past (Cohen, 1983; Gopnik, 1996). Accordingly, Piagetian questions are considered nowadays to be irrelevant to current developmental research (Gopnik, 1996; Perner, 1991).
However, “theories of human nature never really die [because] they go in and out of fashion” (Horgan, 1999, pp. 6-7). Thus, the interest in classical theories, such as Piaget’s approach, has come back (Lourenço, 2014, 2016; Miller et al., 2000; Müller et al., 2009), even after the proclamation of its death (Cohen, 1983; Gopnik, 1996). This study is an example of the recent interest in Piaget’s theory in general, and his concern with the idea of logical necessity in particular. The study also shows, as Chapman (1992) cogently remarked, that despite the several strengths of Piaget’s theory (e.g., its constructivist stance) “... The problems with the theory do not disappear when it is better understood” (p. 39).
The present study focuses on Piaget’s (1987a,b; see also Smith, 1993, 2009) views on children’s understanding of the idea of logical necessity. Note that the child’s understanding of the idea of logical necessity is intrinsically related to his/her epistemic status. Thus, when an operational child resists a counter-suggestion and maintains his/her previous operational status and correct answer, s/he shows that both (a) that answer is the case (true knowledge), and (b) it cannot be otherwise (necessary knowledge and logical necessity). In the same vein, when a preoperational child refuses a counter-suggestion and maintains his/her previous epistemic status and incorrect answer, s/he shows that both (a) that answer is the case (false knowledge), and (b) it cannot be otherwise (i.e., pseudo necessity). This is more valid the more the counter-suggestion is demanding. Needless to say, logical necessity and pseudo necessity are concepts advanced by theorists (e.g., Piaget, 1987a,b), not by the child.
However, in order to grasp children’s understanding of the idea of logical necessity in an in-depth way, the present study appealed to procedures different from those employed in previous studies in general (Miller, 1986; Miller et al., 2000; Smedslund, 1961), and Piaget’s (1983, 1987a,b) experiments in particular.
For example, some previous studies have assessed children’s understanding of the idea of logical necessity by examining children’s reaction to disconfirming evidence. For instance, in a Smedslund’s (1961) study, children who had acquired conservation of weight by control on a balance (group 1) and children who had acquired conservation prior to the study (group 2) showed some instances of apparent non-conservation. All children in group 1 easily gave up their concept of conservation and reverted to more primitive perceptual strategies. About half of the children in group 2 resisted the attempt for extinction and interpreted the apparent non-conservation as implying that something was added to or taken away from one of two clay balls.
The present study employs two types of counter-suggestion to analyze in a detailed way children’s epistemic status and, hence, their understanding of the idea of logical necessity. For example, when a preoperational child refuses a Piagetian counter-suggestion, s/he is showing that his/her previous incorrect answer on a given task had to be the case and could not be otherwise (i.e., pseudo necessity). In the same vein, when an operational child refuses a Piagetian counter-suggestion, s/he is showing that his/her previous correct answer had to be the case and could not be otherwise. Needless to say, logical necessity and pseudo necessity are concepts advanced by theorists (e.g., Piaget, 1987a,b), not by the child.
Obviously, the more a counter-suggestion is challenging and demanding, the more it “perturbs” the child’s cognitive equilibrium and, hence, the more it allows us to see to what extent children believe that their knowledge about a certain issue has/has not to be necessarily the case. Thus, when operational children refuse a demanding counter-suggestion, an adult’s counter-suggestion, for example, they have a more developed understanding of the idea of logical necessity than when they refuse a less demanding counter-suggestion, a child’s counter-suggestion, for instance. Generally speaking, adults are epistemic authorities for children (Piaget, 1932). Even so, according to Piaget’s (1983) constructivist theory, children’s acceptance of an adult’s perspective is never an uncritical acceptance or a mere social submission. This is particularly visible in some of the moral development literature, namely in Turiel’s (1983) social domain approach and its focus on the child’s distinction between morality and convention. In this approach, it has been found that children as young as four or even younger reject adults’ views when adults say, for instance, that it is all right to steal, to hit, and the like. Will it be that children’s sense of moral obligation comes first than their sense of logical necessity? Note, however, that the idea of moral obligation in the moral domain corresponds by and large to the idea of logical necessity in the cognitive domain (see Piaget, 1932). Be that as it may, social domain findings show that adults are not always indisputable authorities for children.
In what follows, we analyze Piaget’s procedures to grasp through his clinical method (Piaget, 1929; see also Bond & Tryphon, 2009) the child’s operational status and, hence, his/her understanding of the idea of logical necessity linked to such a status. To capture children’s operational status and understanding of logical necessity, Piaget (1929) used three original procedures: (1) perceptual seductions; (2) justifications; and (3) counter-suggestions.
Perceptual seductions are attempts to deceive the child by introducing salient and easy-to-note transformations into the initial system. For example, in order to avoid minimal perceptual seductions on a number conservation task involving two rows of buttons in one-to-one correspondence, Piaget (Piaget & Szeminska 1980) never put a small number of elements in each row (e.g., less than five/six buttons). Piaget’s set-up ensures that preoperational answers based on perceptual recognition are not taken for operational answers based on operational construction.
As for perceptual seductions, Piaget could hardly have gone further. Suffice it to say that the transformation he introduced into his tasks during his clinical interview was salient in perceptual terms and, hence, suitable for leading to the child’s cognitive “perturbation”. “How can a clearly elongated row with six buttons – the child may ask – have the ‘same thing’ of buttons than a clearly non-elongated row with six buttons too?”.
When the child is asked to justify his/her responses on a typical Piagetian task, the child is required to give reasons for her/his answers to the questions involved in the task at hand. According to Piaget (1983), preoperational children justify their answers through functional arguments, that is, arguments based, for example, on the spatial arrangement of the elements on a number conservation task. In contrast, operational children justify their answers through operational arguments (i.e., identity, reversibility, compensation), that is, arguments based on the logic underlying the competence at hand (e.g., to recognize that the quantity of elements in a set remains constant regardless of their spatial configuration in the respective set; Inhelder, Sinclair, & Bovet, 1974; Piaget & Inhelder, 1969a). In Piaget’s (1983) theory, operational arguments are to logical necessity – what is the case and has to be the case – as functional arguments are to pseudo necessity – what seems to be necessarily the case, but it cannot be the case.
We also think that Piaget could hardly have gone further regarding children’s justifications on his multiple tasks. Thus, when Piaget asked children to justify their answers, he either led them to explain why they answered in that way, or why they knew that their answer is that one they had given shortly before.
However, Piaget might have gone further than his standard counter-suggestions to obtain an in-depth, albeit indirect, assessment of children’s idea of logical necessity. An in-depth mapping of preoperational and operational children’s sense of the idea of logical necessity is the main goal of this research. To attain this goal, we used two novel types of counter-suggestion on two conservation tasks. In spite of the voluminous literature on conservation and logical necessity (Bibok, Müller, & Carpendale, 2009; Caroff, 2002; Miller et al., 2000; Overton, 1990), we know of no study that employed the present approach and methodology. It is noted that this study, strictly speaking, is not a conservation study despite the fact that conservation tasks were used. Conservation tasks here are a means to our main aim of exploring children’s understanding of the idea of logical necessity. Instead of conservation tasks, class-inclusion or transitivity tasks, for example, could be used for that purpose.
In a typical Piagetian counter-suggestion, the interviewer confronts children with an answer opposed to the answer they gave to the critical of the question focal task. The opposite answer was supposedly given by a putative age-peer of the examinee. However, this putative child is not asked to justify her disagreement with the interviewed child. Because of this, such counter-suggestion may hinder the child’s manifestation of his true epistemic status and sense of logical necessity. Actually, a non-justified counter-suggestion coming from a putative child is less challenging than a justified counter-suggestion coming also from a putative child because the former provokes less cognitive disequilibrium in the interviewed child than the latter. As such, it is reasonable to think that the more the interviewed child refuses a justified counter-suggestion, the more s/he seems to be sure about the logical necessity involved in his/her previous answer.
In what follows we describe the two novel types of counter-suggestion mentioned above. The first type of counter-suggestion confronts the child with an answer opposed to her/his previous response to the critical question of the focal task. In this experimental counter-suggestion, the opposite answer belongs to a putative child of the same age as the interviewed child. This opposite answer is justified, additionally, by an appropriate argument: a functional argument when the examinee gives an operational response to the critical question of the focal task; an identity argument when the examinee gives a preoperational response.
Although we return to the reasons why we used the identity argument in this counter-suggestion, here it is noted that such procedure has much to do with some philosophers’ (e.g., Meyerson, 1960) and psychologists’ (e.g., Bruner, 1966) views on the relevance of identity for one’s logical thinking and, to a lesser extent, with Piaget’s views (Piaget, 1966; Piaget & Inhelder, 1974) on the role of his operational arguments in the individual’s operational and logical thinking.
The second type of counter-suggestion confronts children with an answer opposed to the one that they gave to the critical question of the task. The opposite answer supposedly comes from a knowledgeable adult who does not justify his disagreement with the examinee.
We assume that the second type of counter-suggestion is more challenging than the first. In their social relations with others, children generally see adults as more powerful epistemic authorities than their peers and, hence, authorities whose viewpoints should be taken into account (Heritage & Raymond, 2005; Piaget, 1932). So, the more children refuse this type of counter-suggestion, the more they can be credited with a sense of logical necessity.
Based on the preceding considerations we formulated the first three hypotheses of this study. First, we predicted that not all children would operate at the same level (preoperational or operational) on both tasks. Therefore, in these children there would be a significant change in their epistemic status and sense of logical necessity from the pre-experimental to experimental phase. Second, we predicted that both preoperational and operational children, especially the former, would be prone to accept the adult’s experimental counter-suggestion more than the child’s experimental counter-suggestion. Third, we predicted that among the three operational arguments, the identity argument would be the most frequently invoked by operational children on both the pre-experimental and the experimental task.
What follows shows that although our third hypothesis is consistent with some philosophers’ (e.g., Meyerson, 1960) and psychologists’ (e.g., Brunner, 1966) views on the role of identity in one’s logical thinking, the hypothesis is not at complete variance with Piaget’s views on the emergence and importance of his operational arguments for one’s operational understanding and sense of logical necessity. In addition to this, the third hypothesis relates to a critical but unclear issue in Piaget’s theory.
On some occasions, Piaget (1966) considered reversibility (by inversion) rather than identity or compensation (i.e., reversibility by reciprocity) the essential property of mental operations. On other occasions, Piaget (Piaget & Inhelder, 1974, Introduction) admitted that longitudinal analyses showed that these three arguments are highly related and appear concurrently rather than in a systematic sequence. This implies that Piaget’s (1966) views on the psychogenesis and importance of any of his operational arguments are relatively ambiguous. Because of Piaget’s concurrent and relational thesis regarding his operational arguments, our third hypothesis is somehow consistent with his theory. Suffice it to say that (a) Piaget’s concurrent thesis admits all variations in the order of manifestation of his operational arguments, according to the situations and subjects examined; and (b) his relational thesis admits that any operational argument may be equally important for one’s operational status and sense of logical necessity. Note, however, that to appear first in development does not mean to be logically priori to what appears later. Preoperational thinking appears first than operational thinking, yet the latter has logical priority over the former.
Like the French philosopher Meyerson (1960) and authors of the “identity theory” (e.g., Acredolo, 1981; Bruner, 1966), one might think that: identity is quintessential to: (a) Piagetian conservations; (b) one’s sense of logical necessity; and (c) and the most fundamental property of logical thinking, and hence, a sine qua non condition of reversibility and compensation. Actually, how would it be possible to nullify a modification introduced into a given system (e.g., to elongate one of two rows of buttons) by an inverse (i.e., reversibility by negation) or compensation operation (i.e., reversibility by reciprocity) if the number of buttons in the elongated row did not stay the same number after the modification? Bruner (1966) even argued that Piaget “... missed the heart of conservation” in that conservations’ roots could be found in “some primitive sense of [quantitative] identity” (p. 186; italics added).
Our fourth hypothesis has to do with an issue raised by many authors to Piaget’s (1983) theory. According to them (Brainerd, 1978; Inhelder & Cellérier, 1992), because of Piaget’s concerns with epistemological problems (Piaget, 1950a,b,c), his theory relies excessively on an epistemic subject at the cost of a psychological subject. Whereas the former solves Piagetian tasks with basis on what all subjects have in common (e.g., their operational competence), the latter solves such tasks by what all subjects do not have in common (e.g., performance factors; Brainerd, 1978; Bryant & Trabasso, 1971; Flavell, 1963; Gelman & Baillargeon, 1983). Although he had emphasized the role of the epistemic subject in the child’s idea of logical necessity and performance on his multiple tasks, Piaget (2004) also gave a role to the psychological subject in that idea and performance (see Piaget & Szeminska, 1980, p. 193).
In contrast to a number conservation task wherein there are discontinuous elements that may be counted and, therefore, facilitate the invocation of the identity argument, a liquids conservation task, because it involves continuous quantities, may hinder the invocation of such argument and facilitate, for example, the invocation of the compensation argument. Therefore, our hypothesis four predicts the following: (a) the number conservation task is the task wherein operational children more often invoke the identity argument; (b) the liquids conservation task is the task wherein operational children more often invoke the compensation argument; and (3) the reversibility argument should be frequently invoked by operational children on both tasks. Given that preoperational children always justify their answers through functional arguments, the fourth hypothesis does not take these arguments into account.
Method
Participants
To ensure the desired experimental sample (40 preoperational and 40 operational children), we examined participants aged between 5 and 7 years. Although in Piaget’s theory, age is an indicator, not a criterion of development, these ages are appropriate to find out preoperational and operational children. To obtain the desired numbers, one hundred children participated in the pre-experimental phase. Fifty-one children were pre-schoolers (Mage=5.40 years, SD=0.67), and 49 children were second graders (Mage=6.67 years; SD=0.88).
Of these 100 children, only 80 (40 preoperational, Mage=5.20, SD=0.65, and 40 operational Mage=6.80, SD=0.64) participated in the experimental phase. In the experimental sample, there were approximately equal numbers of girls (42) and boys (38). Seventeen 6-year-old children were excluded from the experimental phase because they were classified as intermediate in the pre-experimental task. We assumed that intermediate children could not be confronted with the above mentioned experimental counter-suggestions. Two 5-year-old children were excluded from this phase because they were not able to understand what was at issue on the number conservation task. One child was excluded because of a misapplication of the task by the interviewer.
All children were white. They were randomly recruited from private schools in the area of Leiria, Portugal, and came from upper-middle-class families. All children’s parents gave written permission to interview their children by using an appropriate consent form. Parents were assured that this research would follow all ethical procedures approved by the Psychological Association from their country and even by the American Psychological Association (APA, 2010).
Experimental design
In the experimental phase, we used a 2x2 between-subjects design: 2 (preoperational and operational children, such as assessed on the pre-experimental phase) x 2 (adult’s vs. child’s experimental counter-suggestion). Specifically, half of the preoperational (20) and the operational (20) children were confronted, respectively, with a counter-suggestion coming from a child and justified through the identity argument vs. a functional argument. The other half of the preoperational (20) and operational (20) children were confronted with a non-justified countersuggestion coming from a knowledgeable adult.
Tasks, material, procedure, scoring, and measures of the dependent variable
We assessed children’s initial epistemic status and sense of logical necessity through a number conservation task (Piaget & Szeminska, 1980). Here, we employed the typical Piagetian clinical method. In the experimental phase, the child’s operational status and sense of logical necessity was assessed through a liquids conservation task (Piaget & Inhelder, 1974). Here, we also followed the Piagetian clinical method, but employed the two novel types of experimental counter-suggestions referred to above. We used a number conservation task in the pre-experimental phase and a liquids conservation task in the experimental phase because the former, which involves discontinuous quantities, is easier than the latter, which involves continuous quantities (see Piaget & Inhelder, 1969b). Moreover, it would not make sense to use an experimental task that was easier than the pre-experimental task. If this were the case, it would be impossible to disentangle the possible effects of the counter-suggestions from the ease of the experimental task on children’s epistemic status and, by implication, their understanding of the idea of logical necessity.
In the number conservation task, there were two rows, the child’s row (CR) and the interviewer’s (IR), each containing six white buttons in one-to-one correspondence. In the liquids conservation task, there were three transparent glasses, two equally low and wide, glasses A and B, and a third glass, C, which was taller and narrower than the other two. There was also a jar to pour water to the glasses.
In both phases children were interviewed by two psychology graduate students. Each interview lasted about 20 minutes. The child’s responses were tape recorded and transcribed for later coding. The interviewers or experimenters (E) were not aware of the hypotheses of the study. All of children’s answers and justifications were coded by two independent judges. The percentage of agreement between the two coders for children’s several answers and justifications was calculated through the index Kappa, which is considered to be a good measure of inter-rater reliability for nominal variables (see Appelbaum & McCall, 1983). This statistical procedure showed that, overall, there was 99.8 percent agreement between the coders for the several types of children’s answers/judgments, and 96.9 percent agreement for children’s justifications. Disagreements were resolved by discussion between the two coders.
a) Presentation of tasks: “On this table there two rows of buttons/two glasses (E points to CR and IR/A and B), each containing the ‘same thing’ of buttons/drinking water. We have also an empty glass (E points to C, in the case of the liquids conservation task)”.
b) Initial question: After presenting the number conservation task to the child, E asked the following: “In which row is there more buttons: Here (E points to CR); there (E points to IR), or are there ‘the same thing’ of buttons in both rows (E points to CR and IR), and why?” All children, with the exception of those excluded from the experimental phase, answered that there was the “same thing” of buttons in each of the two rows, and gave appropriate reasons to justify their answers (e.g., “there is ‘the same thing’ of buttons in both rows because there are six buttons in each row”). The same procedure was used for the liquids conservation task. Thus, these participants showed to understand the problem at hand.
c) Transformation of the initial system and presentation of the critical question and justification. E passes the drinking water from glass A to glass C, calls the child’s attention to this passage, and asks her/him the following: “In which glass is there more drinking water: Here (E points to C); there (E points to B), or is there ‘the same thing’ of drinking water in both glasses (E points to C and B), and why?” The same procedure was used in the liquids conservation task.
Children’s answers and justifications on each task were coded according to the well-known Piagetian coding system (see Piaget & Inhelder, 1969a): Preoperational, if children answered incorrectly and justified their answer by a functional argument (e.g., “There is more drinking water in this glass – tall and narrow – than in that one – low and wide – because the water gets higher in the first than the second glass”); Operational, if children answered correctly and justified their answer by an operational argument: identity (e.g., “There is the ‘same thing’ of buttons/drinking water in both rows/glasses because no button/drinking water was added to, or taken away from, any row/glass); reversibility (e.g., “There is the ‘same thing’ of buttons in both rows because one can return the elongated row to its initial form”); or compensation (e.g., “There is ‘the same thing’ of drinking water in B and C because when one passes the drinking water from A to C, the drinking water gets higher in C than B, but, at the same time, C is narrower than B”); Intermediate, if, for example, children gave a correct answer to the critical question but did not justify their answer through an operational argument. It is reminded that intermediate children did not participate in the experimental phase because it would be difficult, if not impossible, to confront them with any experimental counter-suggestion.
d) Presentation of an appropriate counter-suggestion: After getting the child’s response and justification mentioned in (c), E confronted the child with a counter-suggestion: A typical Piagetian counter-suggestion on the number conservation task; one of the two types of experimental counter-suggestions on the liquids conservation task. An example follows: “You said that now (i.e., after the transformation of the initial system) there are more buttons here (elongated row) than there (non-elongated row) because in the first row the buttons occupy more space than in the second row. However, a boy/girl, as old as you, told me shortly before that there is the ‘same thing’ of buttons in both rows. Are you right, is s/he right, or might you both be right, and why?”.
This procedure was also followed on the liquids conservation task. But now the countersuggestion was presented as belonging to (a) a putative child who justified his/her disagreement with the experimental child by either invoking the identity argument in the case of a preoperational child, or a functional argument in the case of an operational child; (b) a knowledgeable adult who did not justify her disagreement with the child being interviewed (preoperational or operational).
Children’s reactions to the presented counter-suggestion were coded as Refusal, if the child maintained her answer to the critical question of the task at hand and gave a justification consistent with such refusal (i.e., a functional justification in the case of preoperational children; an operational justification in the case of operational children); Acceptance, if the child changed his/her answer to that question, and gave an argument consistent with such acceptance; and Hesitation, if the child oscillated between keeping his/her response to the critical question of the focal task and adhering to the presented counter-suggestion. This means that in the passage from the number conservation to the liquid conservation task there was Maintenance, when the child refused the respective counter-suggestion; or Change, when the child accepted the respective counter-suggestion or hesitated between refusing the counter-suggestion and accepting it. This change in the child’s epistemic status and correlative sense or idea of logical necessity could be an Upward change (e.g., from a preoperational and pseudo necessity-oriented answer to an operational and logical necessity-oriented answer) or a Downward change (e.g., from an operational and logical necessity-oriented answer to a preoperational and pseudo necessity-oriented answer).
Children’s justifications of their responses to the critical question on both tasks and of their reactions to the presented counter-suggestion were classified as Functional, if children justified their responses and reactions by a functional argument, or Operational, if children justified their reactions and responses by an operational argument.
In this study, there were three measures of the dependent variable: (1) preoperational and operational children’s reactions to each one of the two experimental counter-suggestions; (2) children’s change/maintenance of their epistemic status and sense of logical necessity from the pre-experimental to the experimental phase; (3) the operational argument invoked by operational children in the pre-experimental and experimental phases. Here, it is noted that each of these measures can be taken as an indicator of the child’s sense of logical necessity. If, for example, a child judged to be operational on the liquids conservation task accepts any type of experimental counter-suggestion, then one may conclude that his/her sense of logical necessity still is relatively low and, thus, not yet well-established.
Results
Nonparametric statistics (e.g., Fisher’s exact test and binomial tests; see Achenbach, 1978) were performed because all measures were categorical or nominal. In contrast to the frequency of refusal responses, the frequency of acceptance and hesitation responses was relatively low. Thus, we combined acceptance responses with hesitation responses in order to have dichotomous categories (refusal vs. acceptance plus hesitation or non-refusal) and performed the just mentioned statistical tests.
Children’s reactions to the experimental counter-suggestions
Table 1 presents the frequency of children’s reactions to the experimental counter-suggestions as a function of their epistemic status on the pre-experimental task and the type of experimental counter-suggestion presented in the experimental task.

Analysis of the data in Table 1 shows that: (a) not all children classified as preoperational or operational on the pre-experimental task were, respectively, preoperational or operational on the experimental task. Actually, 22 children gave non-refusal answers in the experimental phase; (b) change occurred in three of the four experimental groups. Therefore, not all children categorized as preoperational or operational in the pre-experimental phase had an established sense of pseudo necessity and logical necessity, respectively, when they were confronted with the respective experimental counter-suggestions. If this were not the case, then there would be only refusal answers in the experimental phase, which was not the case. This finding is statistically significant (p<0.001, N=80, binomial test).
To sum up, as predicted, the experimental suggestions had a significant effect on children’s epistemic status and their understanding of the idea of logical necessity.
Change in children’s epistemic status and sense of logical necessity from the pre-experimental to the experimental phase
Table 2 presents the number of children who maintained or changed (upwards or downwards) their operational status and sense of logical necessity in the experimental phase as a function of the experimental counter-suggestions and the child’s operational status in the pre-experimental phase. In Table 2, children’s answers of acceptance were combined with children’s answers of hesitance. This combination generated a single category – change (upwards or downwards).

An analysis of the data in Table 2 reveals three patterns: (1) Preoperational and operational children changed more their epistemic status and understanding of the idea of logical necessity when they were confronted with the experimental counter-suggestion given by an adult rather than a child. This difference was statistically significant in operational children (p<0.003), but only marginally significant in preoperational children (p<0.096; Fisher’s exact test in both cases). (2) Preoperational children changed their epistemic status and sense of (pseudo) logical necessity more than their operational counterparts when they were confronted with the child’s experimental counter-suggestion. This difference, however, was not statistically significant (p>0.05; Fisher’s exact test). In contrast, operational children changed their epistemic status and sense of logical necessity less than their preoperational counterparts when they were confronted with the expert adult’s counter-suggestion. This difference, however, was not statistically significant either (p>0.05; Fisher’s exact test (3). The occurrence of refusal answers was significantly high in both preoperational and operational children when confronted with the child’s (p<0.012, N=20; p<0.001, N=20, respectively), rather than the adult’s experimental counter-suggestion (p<0.05, N=20; p<0.05, N=20, respectively; binomial tests in all cases).
In summary, a significant change in children’s epistemic status and understanding of the idea of logical necessity from the pre-experimental to the experimental phase occurred only in the whole set of the experimental children. As can be seen in Table 2, this change was an upward change in 14 preoperational children, and a downward change in 8 operational children. In addition, as predicted children refused the adult’s experimental counter-suggestion less than the child’s experimental one, this finding being more visible in preoperational than operational children.
Operational arguments invoked by operational children
Table 3 presents the frequency of each operational argument invoked either in the justification of their responses to the critical question of each task or the justification of their reaction to the presented counter-suggestion.
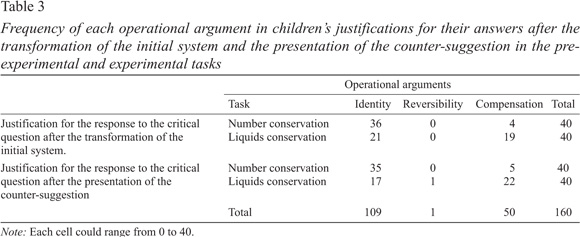
An analysis of the data in Table 3 shows that (a) there was a statistically significant difference between the total number of identity arguments (109), and the total number of compensation arguments (50; p<0.001, N=160; binomial test). The high occurrence of the identity argument lends support to the third hypothesis of this study (i.e., among the three operational arguments, the identity argument would be the more frequently invoked argument by operational children on both the pre-experimental and experimental tasks). (b) In the number conservation task, the identity argument was significantly more frequently invoked than the compensation one (p<0.002, N=40; binomial tests in all cases). This is to be contrasted to the liquids conservation task, where there were no statistically significant differences between the arguments of identity and compensation in either children’s justifications for their answers to the critical question of the focal task, or the justifications of their reactions to the presented counter-suggestion (p>0.05, N=40 in both cases). (c) The compensation argument was significantly more frequently invoked by operational children in the liquids conservation task than in the number conservation one. This also occurred in both children’s justifications for their responses to the critical question of the task at hand (p<0.003, N=23), and the justifications for their reactions to the presented counter-suggestions (p<0.002, N=28; binomial tests in both cases).
The results reported in (b) and (c) are consistent with the first two predictions of hypothesis four: The task in which operational children more often invoke the identity argument is the number conservation task; the task wherein operational children more often invoke the compensation argument is the liquids conservation one.
As Table 3 shows, in contrast to the third prediction of our hypothesis four (i.e., the reversibility argument should often be invoked by operational children on both tasks), this argument was practically non-existent in the arguments given by operational children. Thus, the third prediction of our hypothesis four was rejected.
Discussion and conclusions
The main goal of this study was to grasp children’s understanding of the idea of logical necessity by appealing to two types of counter-suggestion that, surprisingly, were rarely, if ever, used by Piaget (1987a, b) or other developmentalists (Miller et al., 2000; Siegal, 1991). We put forth four hypotheses concerning the child’s sense of logical necessity and tested them on two Piagetian conservation tasks.
As predicted by our first hypothesis (i.e., there would be a significant change in preoperational and operational children’s epistemic status and sense of logical necessity from the pre-experimental to experimental phase), many children did change their epistemic status and understanding of the idea of logical necessity on the liquids conservation task (see Tables 1 and 2).
A possible explanation of this change might be to say that the difference between the experimental and the pre-experimental task, rather than the experimental counter-suggestions, was responsible for that change. However, the following finding rules out this possibility: Of the 22 children who changed their epistemic status and sense of logical necessity, 14 were preoperational and showed an upward change (see Table 2). Therefore, this upward change cannot be ascribed to the experimental task, which is more difficult than the pre-experimental task (Piaget & Inhelder, 1969b), but rather to the effect of the experimental counter-suggestions.
It might be objected that it remains to be explained why 8 of the 40 operational children showed a downward change (see Table 2). As this change occurred more in children’s hesitation responses (7) than in children’s acceptance responses (1), one might think that children who showed an “upward hesitation change” are more in route to grasping the next level of epistemic status and sense of logical necessity than those who showed, say, a “downward acceptance change”. Note that an upward hesitation change is above a downward acceptance change because the former is closer to the next level of epistemic status and sense of logical necessity than the latter (see Lourenço, 2016).
One might still think that the above mentioned significant change from the pre-experimental to the experimental phase was due to a training effect of the pre-experimental task on the children’s performance on the experimental task. If this had been the case, it would be difficult to explain why the pre-experimental task had a beneficial effect on preoperational children’s performance on the liquids conservation task, and a detrimental effect on operational children’s performance on this task (see Table 2).
In this study, operational children changed their epistemic status and sense of logical necessity from the pre-experimental to the experimental phase less than their preoperational counterparts. This finding is consistent with the developmental literature (Flavell, 1982, 1992), the literature on suggestibility in children (Saltzstein, Dias, & Millery, 2004), and Piaget’s theory (see Perret-Clermont, 1979; Piaget, 1932, 1985). This literature and theory shows that the more a child is cognitively developed the closer s/he is to a level of cognitive equilibrium and, hence, the less s/he is “perturbed” when confronted with viewpoints different from his/her own.
In summary, it is reasonable to think that if the experimental counter-suggestions had been employed in the pre-experimental phase, then children’s epistemic status and sense of logical necessity on the number conservation task would have not been exactly those that occurred. This means that this study is relevant to the role of counter-suggestions in the child’s performance on Piagetian tasks and his/her understanding of the idea of logical necessity.
The second hypothesis of this study (i.e., both preoperational and operational children would refuse the adult’s experimental counter-suggestion less than the child’s experimental counter-suggestion, this being more visible in preoperational than operational children) was also corroborated. Although the difference between children’s refusal of the two experimental counter-suggestions had been only statistically significant in operational children, both the preoperational and operational children refused the adult’s experimental counter-suggestion less than the child’s experimental counter-suggestion (see Table 1).
This finding is consistent with Piaget’s theory which assumes that adults are a source of epistemic authority, especially for young children. Even so, in contrast to a widespread idea that sustains that, according to Piaget’s theory, children accept uncritically adults’ viewpoints (see Siegal, 1991) the present study assumes that such an idea is at odds with the constructivist assumptions that lie at the heart of his theory. This means that to confront children with adult’s viewpoints is a justifiable and good procedure to grasp children’ epistemic status and sense of logical necessity and does not amount to employing a procedure that leads to results that, say, are known before that confrontation.
Thus, as predicted, counter-suggestions coming from a knowledgeable adult were more challenging than those coming from a child who justified through an appropriate argument her/his disagreement with the interviewed child on the issue at hand (see Table 2). This result helps us understand why the adult’s counter-suggestion led 18 children to change their epistemic status and sense of logical necessity, whereas the child’s counter-suggestion led only 4 children to modify their epistemic status and sense of logical necessity (see Table 2). It is understandable that the influence of the adult’s counter-suggestion on children’s performance on the liquids conservation task has been found to be more evident in preoperational than operational children. Preoperational children are still at a stage of cognitive development relatively unbalanced in terms of cognitive equilibrium (Piaget, 1985, 2001). This fact may have provoked more cognitive “perturbation” in preoperational than operational children when they both were confronted with the adult’s countersuggestion.
Our third hypothesis predicted that among the three operational arguments, the identity argument would be the most frequently invoked by operational children on both the pre-experimental and the experimental task. This was found to be the case (see Table 3). It is well understandable that the identity argument had been often invoked by operational children on the number conservation task (71) because the task deals with discontinuous quantities that can be counted and, hence, facilitate identity justifications. As this argument often appeared on the liquids conservation task (38), which deals with continuous quantities, it seems that the invocation of the identity argument is not only due to a counting effect.
This finding is consistent with philosopher Meyerson’s (1960) and the identity theory authors’ (e.g., Bruner, 1966) views that conservations’ and logical necessity’ roots could be found in some primitive sense or idea of quantitative identity. As Piaget admitted that there is a solidarity among the three operational arguments, with all the variations in the order of their manifestation, according to the situations and subjects examined (see Piaget & Inhelder, 1974), the high frequency of the identity argument is not at complete variance with Piaget’s theory. Note also that identity may be a source of logic necessity because it suggests stability and consistency (Demetriou, Makris, Kazi, & Spanoudis, 2018).
The fact that the identity argument has been more invoked on the number conservation than the liquids conservation task, and that the argument of compensation has appeared more often in the latter than the former (see Table 3) shows that the so-called psychological subject and content have a role in Piaget’s (2004) theory. As Chapman (1988, pp. 348-356, 364-368) cogently argued, Piaget’s theory is essentially structural, but it also involves functional aspects. Thus, the above mentioned fact is not in accordance with some of Piaget’s critics (Braine, 1959; McGarrigle, Grieve, & Hughes, 1978) who faulted his theory for giving no role to performance factors in the individual’s operational thinking. The present study shows that such a criticism should be seen cautiously. Suffice it to say that the late Piaget (1986) admitted that that formal individuals can be formal in certain domains (e.g., their area of expertise), but not in other domains.
The third prediction of our hypothesis four (i.e., the reversibility argument would be often invoked by operational children on both tasks) was rejected because this argument was invoked only once. In contrast, the other two points of our hypothesis four (operational children would often invoke the identity argument on the number conservation task; the compensation arguments on the liquid conservation task) were substantially corroborated (see as Table 3).
The fact that the argument of reversibility appeared only once is surprising because of Piaget’s thesis that (a) the three operational arguments are intertwined and found in all forms of conservation (Piaget & Inhelder, 1969b, Introduction), and (b) reversibility is the essential property of the operations which characterize living logic in action (Piaget, 1966).
One can understand that the reversibility argument has not appeared on the number conservation task because it involves discrete quantities that can be counted and, therefore, facilitate the appearance of identity justifications (71) and hinder the appearance of reversibility justifications. As can be seen in Table 3, this seemed to be the case. Similarly, one may understand that reversibility justifications have not practically appeared on the liquid conservation task because in this task the drinking water is contained in glasses whose increase in tallness compensates for their decrease in width. This fact can facilitate the invocation of compensation justifications (41) and hinder the invocation of reversibility justifications (1). Again, as can be seen in Table 3, this seemed to be the case.
The high frequency of the identity argument in the present study is consistent with Meyerson’ (1960) and Bruner’s (1966) views on the central role of identity in one’s logical thinking. As mentioned, according to Bruner (1966), conservations’ and logical necessity’ roots are not to be found in reversibility, but rather in some primitive sense or idea of quantitative identity. This frequency does not fit with Piaget’s thesis that (a) the three operational arguments are found in all forms of conservation; (b) these arguments are deeply intertwined; and (b) reversibility is the essential characteristic of logical and operational thinking (see Piaget, 1966; Piaget & Inhelder, 1969a).
The second prediction of hypothesis four (i.e., the compensation argument would be more invoked on the liquids conservation than on the number conservation task) was significantly corroborated (see Table 3). Here it might be said that this research is focused on the child’s understanding of logical necessity, and yet it elaborates a lot on children’s invocation of operational arguments. However, like Piaget (1987a,b), we assume that the child’s invocation of operational arguments is necessarily linked to her sense of logical necessity. It suffices to say that a conserving child on a number conservation task, for example, always says that her answer on that task has to be the case and justifies her operational answer by saying that it cannot be otherwise because nothing was added to, or taken away from, the initial system (identity); it is possible to return to a non-elongated row (reversibility); the elongated row occupies more space but it contains fewer buttons in a given space (compensation). In other words, operational children are to their operational status, idea of logical necessity, and appeal to operational arguments such as preoperational children are to their preoperational status, idea of pseudo necessity and appeal to functional arguments. The link among the child’s operational status, her sense of logical necessity and her grasp of operational arguments renders an independent assessment of each of these issues unnecessary.
The third point of our hypothesis four (i.e., the reversibility argument would be often invoked by operational children on both tasks) was rejected because this argument was invoked only once. In contrast, the other two predictions of our hypothesis four (i.e., operational children would often invoke the identity argument on the number conservation task; operational children would often give compensation arguments on the liquid conservation task) were substantially corroborated as can be seen in Table 3.
The fact that the argument of reversibility appeared only once is surprising because of the above mentioned Piaget’s thesis that the three operational arguments are profoundly intertwined and found in all forms of conservation (Piaget & Inhelder, 1969b, Introduction), and that reversibility is the essential property of the operations which characterize living logic in action (Piaget, 1966). It is possible that the reversibility argument had not been invoked by children because it is more difficult to be verbalized than the identity and compensation arguments. Although we have no data to reject this possibility, it does not seem very plausible. Actually, to say that the elongation of one of two rows, each containing the “same thing” of buttons in one-to-one correspondence, can be cancelled by an inverse operation does not seem more difficult than saying that: (1) the elongated row has the “same thing” of buttons as the non-elongated one because no button was added to, or taken away from, the initial system (i.e., identity argument); (2) the elongated row occupies more space than the non-elongated one, but in the elongated row there are fewer buttons in a given space than in the non-elongated row (i.e., compensation argument).
It is rare to find a research that raises no problems, contains no limitations, and does not point to examples for future research. What follows elaborates on these three issues.
For example, one might say that the title of this study refers to children’s understanding of the idea of logical necessity, yet the study elaborates a lot on children’s operational status and their grasping of the operational arguments on two conservation tasks. An answer to this objection would be to say that in Piaget’s (1987a,b) theory the individual’s understanding of logical necessity is closely related to his/her epistemic operational status and grasp of the operational arguments.
For instance, it might be argued that although this study allow us to conclude that children’s change in their epistemic status and understanding of the idea of logical necessity from the pre-experimental to the experimental phase was due to the experimental counter-suggestions, a more rigorous test for explaining the occurrence of that change would be, for example, to carry out a research in which the pretest task would be the same as the posttest task. This type of research may be an example of future research on the issues addressed in the present study. However, in this type of research it would be difficult, perhaps impossible, to separate a possible training effect from a possible counter-suggestion effect on the child’s epistemic status and understanding of logical necessity.
No doubt, children’s epistemic status and sense of logical necessity in the pretest could have been determined through several Piagetian tasks, not only through a number conversation task. Given that both preoperational and operational children on a given Piagetian task are not necessarily also preoperational or operational on another task (see Piaget & Szeminska, 1980, p. 186), it would be difficult to form an experimental sample composed, for example, of 40 preoperational and 40 operational children if several Piagetian tasks were used in the pretest. Note, however, that the developmental literature (Bryant & Travasso, 1971; Piaget, 1983; Siegal, 1991) is full of examples wherein the child’s epistemic status is determined through a single task. In addition, as this study uses novel counter-suggestions, it is exploratory in its very nature.
It might be also argued that if children, who produced identity and compensation justifications, would have been asked to think of another justification, many of them might have articulated some form of reversibility. This can be another example of future research. However, one may think that reversibility, identity, or compensation justifications due to additional questioning would risk being more suggested than spontaneous justifications.
Of course, additional forms of counter-suggestions might here be helpful. Presumably, the more counter-suggestions a reputedly concrete operational child can refuse, the more likely it is that the child is, in fact, operational and has a true sense of logical necessity. This procedure, however, is not without problems. To confront a child with several counter-suggestions may lead the child to think that his/her previous answer was not right and, hence, s/he has to react differently when a subsequent counter-suggestion is presented.
It might still be argued that counter a suggestion coming from real, not hypothetical interlocutors, would be more challenging and appropriate to assess children’s sense of logic necessity. Although accepting that this is a limitation of the present study, relevant developmental literature (e.g., Piaget, 1983; Turiel, 1983) uses hypothetical counter-suggestions. Even so, future research can address this limitation. Note, however that, as shown by the classical Asch (1955) conformity experiments, real interlocutors are more likely to lead to conformity than their hypothetical counterparts.
To our knowledge, there is no study that has counted the frequency of each operational argument in children’s performance on Piaget’s conservation tasks. Because of this, we cannot compare the present findings with findings of previous studies such that it was possible to see to what extent the current findings are consistent/inconsistent with results of those previous researches.
We have no definite thesis about the importance of each operational argument to characterize the child’s operational status and his/her understanding of logical necessity with basis on its respective invocation by children. However, it makes sense to think that the more a child invokes a given operational argument, the more this argument is likely to be relevant to determine his/her epistemic status and understanding of logical necessity. To carry out a research to address this issue would be another example of future research.
As far as we know, the epistemic power of each operational argument to bring about changes in the child’s understanding of the idea of logical necessity was rarely, if ever, studied. A possible research to address this issue could be the following: (1) to have three experimental groups of preoperational children on a given Piagetian task, for example, a liquids conservation task. (2) To see to what extent children’s preoperational responses to the critical question of that task would become intermediate or operational answers when children were confronted with a counter-suggestion justified by the identity argument (group 1); by the reversibility argument (group 2); and by the compensation argument (group 3).
More than ever, neurosciences are giving rise to many empirical studies and theoretical debate in the domain of psychology (e.g., Gazzaniga, 2005; Zelazo, Chandler, & Crone, 2010). A possible way of knowing whether or not the three Piagetian operational arguments have the same operational power or effect on children’s performance on a given Piagetian task would be to register through an appropriate procedure the brain activity associated with the invocation of each operational argument. An appropriate method could be to utilize functional magnetic resonance imaging (fMRI), a procedure that measures brain activity by detecting associated changes in blood flow (see Eslinger & Robinson-Long, 2010).
Nowadays, articles on Piaget’s theory are generally considered to be out of fashion. So, as would be expected, neo-Piagetian theories, such as Case’s (1985) theory of intellectual development, post-Piagetian theories, such as Commons, Richards and Armon’s (1984) model of cognitive development, anti-Piagetian theories, such as Perner’s (1991) approach to children’s theories of mind, and even neo neo-Piagetian theories, such as Bickhard’s (2009) interactive model of development, have appeared. The present study is not at variance with these theories. Like Case’s theory, this study also assumes that young children’s intellectual skills are more concretely than abstractly oriented. This core is also accepted by Demetriou and colleagues’ (2018) recent model of a psychometric/developmental intelligence. Like Commons and colleagues’ (1984) approach, this study also espouses the idea that operational children are more capable than their preoperational counterparts of coordinating several dimensions or perspectives. Like Perner’s (1991) approach, the present study also assumes that operational children are more entitled than their preoperational counterparts to have a more advanced theory of mind. Like Bickhard’s (2009) interactive model, this study also sustains that the child’s epistemic status and understanding of logical necessity is due to an active interaction between the child and his physical and social worlds. However, in contrast with Piaget’s theory and the present study, none of these approaches addresses explicitly the problems involved in children’s understanding of logical necessity.
When analyzing the role of Piaget’s stages in cognitive development, Feldman and Benjamin (2004) spoke about an unfinished symphony. On their view, Piaget’s theory of stages is an unfinished symphony because, for example, its emphasis on stages is made at the cost of the analysis of the processes at issue in the transition from one stage to another. By elaborating on children’s understanding of logical necessity through counter-suggestions that Piaget rarely, if ever, used, the present paper may render that unfinished symphony less unfinished than it seems to be.
Piaget once confessed to Jean Claude Bringuier (1980, p. 140) that he had drawn a general skeleton, but one still full of gaps of such a kind that, in filling them, one will be led to differentiate its connections, in various ways, without at the same time altering the main lines of the system. By addressing children’s understanding of logical necessity through counter-suggestions that Piaget never used in his experiments, this exploratory study may have filled one of such gaps, while maintaining the main lines of the system.
References
Achenbach, T. (1978). Research in developmental psychology: Concepts, strategies, methods. New York: The Free Press. [ Links ]
Acredolo, C. (1981). Acquisition of conservation: A clarification of Piagetian terminology, some recent findings, and an alternative formulation. Human Development, 24, 120-137. [ Links ]
American Psychological Association [APA]. (2010). Publication manual of the American Psychological Association (6th ed.). Washington, DC: American Psychological Association. [ Links ]
Appelbaum, M., & McCall, R. (1983). Design analysis in developmental psychology. In P. H. Mussen (Ed.), Handbook of child psychology (Vol. I, pp. 415-476). New York: Wiley. [ Links ]
Asch, S. (1955). Opinions and social pressure. Scientific American, 193, 35-35. [ Links ]
Beilin, H. (1992). Piaget’s enduring contribution to developmental psychology. Developmental Psychology, 28, 191-204.
Bibok, M., Müller, U., & Carpendale, J. (2009). Childhood. In U. Müller, J. Carpendale, & L. Smith (Eds.), The Cambridge companion to Piaget (pp. 229-254). Cambridge: Cambridge University Press. [ Links ]
Bickhard, M. (2009). Interactivism: A manifesto. New Ideas in Psychology, 27, 85-95. [ Links ]
Bond, T., & Tryphon, A. (2009). Piaget and method. In U. Müller, J. Carpendale, & L. Smith (Eds.), The Cambridge companion to Piaget (pp. 171-199). Cambridge: Cambridge University Press. [ Links ]
Braine, M. (1959). The ontogeny of certain logical operations: Piaget’s formulations examined by nonverbal methods. Psychological Monographs: General and Applied, 73, 1-41.
Brainerd, C. (1978). Piaget’s theory of intelligence. Englewood Cliffs, NJ: Prentice-Hall.
Bringuier, J. (1980). Conversations with Jean Piaget. Chicago: University of Chicago Press. [ Links ] (Original work published 1978)
Bruner, J. S. (1966). On the conservation of liquids. In J. S. Bruner, R. R. Olver, & P. M. Greenfield (Eds.), Studies in cognitive Growth (pp. 183-207). New York: Wiley. [ Links ]
Bryant, P., & Trabasso, T. (1971). Transitivity inferences and memory in young children. Nature, 232, 456-458. [ Links ]
Caroff, X. (2002). What conservation anticipation reveals about cognitive change. Child Development, 17, 1015-1031. [ Links ]
Carpendale, J., & Lewis, C. (2004). Constructing an understanding of mind: The development of children’s social understanding within social interaction. Behavioral and Brain Sciences, 27, 79-96.
Case, R. (1985). Intellectual development: Birth to adulthood. Orlando, FL: Academic Press. [ Links ]
Chapman, M. (1988). Constructive evolution: Origins and development of Piaget’s thinking. Cambridge: Cambridge University Press.
Chapman, M. (1992). Equilibration and the dialectics of organization. In H. Beilin & P. Pufall (Eds.), Piaget’s theory: Prospects and possibilities (pp. 39-59). Hillsdale, NJ: Erbaum.
Cohen, D. (1983). Piaget: Critique and assessment. London & Camberra: Croom Helm. [ Links ]
Commons, M., Richards, F., & Armon, C. (Eds.). (1984). Beyond formal operations. New York: Praeger. [ Links ]
Demetriou, A., Makris, N., Kazi, S., & Spanoudis, G. (2018). Mapping the dimensions of general intelligence: An integrated differential-develpmental theory. Human Development, 61, 4-42. [ Links ]
Eslinger, P., & Robinson-Long, M. (2010). Crucial developmental role of prefrontal cortical systems in social cognition and moral maturation: Evidence from early prefrontal lesions and fMRI. In P. Zelazo, M. Chandler, & E. Crone (Eds.), Developmental social cognitive neuroscience (pp. 251-267). New York & London: Psychology Press. [ Links ]
Feldman, D., & Benjamin, A. (2004). Piaget’s stages: The unfinished symphony of cognitive development. New Ideas in Psychology, 22, 175-185.
Flavell, J. (1963). The developmental psychology of Jean Piaget. Princeton, NJ: Van Nostrand. [ Links ]
Flavell, J. (1982). Structures, stages and sequences in cognitive development. In W. Collins (Ed.), The concept of development (pp. 1-28). Hillsdale, NJ: Erlbaum. [ Links ]
Flavell, J. (1992). Cognitive development: Past, present and future. Developmental Psychology, 28, 998-1005. [ Links ]
Gazzaniga, M. (2005). The ethical brain: The science of our moral dilemmas. New York: Harper Perennial. [ Links ]
Gelman, R., & Baillargeon, R. (1983). A review of some Piagetian concepts. In P. H. Mussen (Ed.), Handbook of child development (Vol. 4, pp. 167-230). New York: Wiley. [ Links ]
Gopnik, A. (1996). The post-Piaget era. Psychological Science, 7, 221-338. [ Links ]
Heritage, J., & Raymond, G. (2005). The terms of agreement: Indexing epistemic authority and subordination in talk-in-interaction. Social Psychology Quarterly, 68, 15-38. [ Links ]
Horgan, J. (1999). The undiscovered mind. NewYork: Free Press. [ Links ]
Inhelder, B., & Céllerier, G. (1992). Le cheminement des découvertes de l’enfant [The child’s process of discoveries]. Lausanne: Delachaux et Niestlé.
Inhelder, B., & Piaget, J. (1958). The growth of logical thinking from adolescence to adulthood. New York: Basic Books. [ Links ] (Original work published 1955)
Inhelder, B., Sinclair, H., & Bovet, M. (1974). Learning and the development of cognition. London: Routledge & Kegan Paul. [ Links ] (Original work published 1974)
Lourenço, O. (2012). Piaget and Vygotsky: Many resemblances and a crucial difference. New Ideas in Psychology, 30, 281-295. [ Links ]
Lourenço, O. (2014). Piaget, Jean. In D. C. Phillips (Ed.), Encyclopedia of educational theory and philosophy (Vol. 2, pp. 623-628). Los Angeles: Sage. [ Links ]
Lourenço, O. (2016). Developmental stages, Piagetian stages in particular: A critical review. New Ideas in Psychology, 40, 123-137. [ Links ]
Lourenço, O., & Machado, A. (1996). In defense of Piaget’s theory: A reply to 10 common criticisms. Psychological Review, 103, 143-164.
McGarrigle, J., Grieve, R., & Hughes, M. (1978). Interpreting inclusion: A contribution to the study of the child’s cognitive and linguistic development. Journal of Experimental Child Psychology, 25, 528-550.
Meyerson, E. (1960). Identity and reality. New York: Dover Publications, Inc. [ Links ] (Original work published 1908)
Miller, A. (1986). Certainty and necessity in the understanding of Piagetian concepts. Developmental Psychology, 22, 3-18. [ Links ]
Miller, A., Brownell, C., & Zukier, H. (1977). Cognitive certainty in children: Effects of concept, developmental level and method of assessment. Developmental Psychology, 13, 236-245. [ Links ]
Miller, A., Custer, L., & Nassau, G. (2000). Children’s understanding of the necessity of logically necessary truths. Cognitive Development, 15, 383-403.
Miller, A., & Lipps, L. (1973). Extinction of conservation and transitivity of weight. Journal of Experimental Child Psychology, 16, 388-402. [ Links ]
Müller, U., Carpendale, J., & Smith, L. (Eds.). (2009). The Cambridge companion to Piaget. Cambridge: Cambridge University Press. [ Links ]
Overton, W. (Ed.). (1990). Reasoning, necessity, and logic: Developmental perspectives. Hillsdale, NJ: Erlbaum. [ Links ]
Perner, J. (1991). Understanding the representational mind. Cambridge, MA: MIT Press. [ Links ]
Perret-Clermont, A. (1979). La construction de l’intelligence dans l’interaction sociale [The construction of intelligence in social interactions]. Berne: Peter Lange.
Piaget, J. (1918). Recherche [Research]. Lausanne: La Concorde. [ Links ]
Piaget, J. (1929). The child’s conception of the world. London: Kegan Paul Trench Trubner. (Original work published 1926)
Piaget, J. (1932). The moral judgment of the child. London: Kegan Paul Trench Trubner. [ Links ] (Original work published 1932)
Piaget, J. (1950a). Introduction à l´épistémologie génétique. Vol. 1: La pensée mathématique [Introduction to genetic epistemology, Vol. 1: Mathematical thinking]. Paris: Presses Universitaires de France. [ Links ]
Piaget, J. (1950b). Introduction à l´épistémologie génétique. Vol. 2: La pensée physique [Introduction to genetic epistemology, Vol. 2: Physical thinking]. Paris: Presses Universitaires de France. [ Links ]
Piaget, J. (1950c). Introduction à l´épistémologie génétique. Vol. 3: La pensée biologique, la pensée psychologique, et la pensée sociologique [Introduction to genetic epistemology, Vol. 3: Biological thinking, psychological thinking, and sociological thinking]. Paris: Presses Universitaires de France. [ Links ]
Piaget, J. (1966). Psychology of intelligence. Totowa, NJ: Littlefield, Adams & Co. [ Links ] (Original work published 1947)
Piaget, J. (1967). Logique et connaissance scientifique [Logic and scientific knowledge]. Dijon: Gallimard. [ Links ]
Piaget, J. (1978). Recherches sur la généralisation [Experiments on generalization]. Paris: Presses Universitaires de France. [ Links ]
Piaget, J. (1983). Piaget’s theory. In P. Mussen (Ed.), Handbook of child psychology (Vol. 1, pp. 103-128). New York: Wiley.
Piaget, J. (1985). The equilibration of cognitive structures. Chicago: Chicago University Press. [ Links ] (Original work published 1975)
Piaget, J. (1986). Essay on necessity. Human Development, 29, 301-314. [ Links ]
Piaget, J. (1987a). Possibility and necessity: The role of possibility in cognitive development (Vol. 1). Minneapolis: University of Minnesota Press. [ Links ] (Original work published 1981)
Piaget, J. (1987b). Possibility and necessity: The role of necessity in cognitive development. Minneapolis: University of Minnesota Press. [ Links ] (Original work published 1983)
Piaget, J. (2001). Studies in reflecting abstraction. Hove: Taylor & Francis. [ Links ] (Original work published in 1977)
Piaget, J. (2004). Reason. New Ideas in Psychology, 24, 1-29. [ Links ]
Piaget, J., & Inhelder, B. (1969a). The psychology of the child. New York: Basic Books. [ Links ] (Original work published 1966)
Piaget, J., & Inhelder, B. (1969b). Intellectual operations and their development. In P. Fraisse & J. Piaget (Eds.), Experimental psychology: Its scope and method (Vol. 7, pp. 147-203). London: Routledge and Kegan Paul. [ Links ] (Original work published 1963)
Piaget, J., & Inhelder, B. (1974). The child’s construction of quantities. London: Routledge & Kegan Paul. (Original work published 1941)
Piaget, J., & Szeminska, A. (1980). La genèse du nombre chez l’enfant (6ème éd.). [The child’s conception of number]. Neuchâtel: Delachaux et Niestlé. (Original work published 1941)
Ricco, R. (1990). Necessity and the logic of entailment. In W. Overton (Ed.), Reasoning, necessity, and logic: Developmental perspectives (pp. 45-65). Hillsdale, NJ: Erlbaum. [ Links ]
Saltzstein, H., Dias, M., & Millery, M. (2004). Moral suggestibility: The complex interaction of development, culture and contextual factors. Applied Cognitive Psychology, 18, 1079-1096. [ Links ]
Siegal, M. (1991). Knowing children. Hillsdale, NJ: Erlbaum. [ Links ]
Smedslund, J. (1961). The acquisition of conservation of substance and weight in children. I: Introduction. Scandinavian Journal of Psychology, 2, 11-20. [ Links ]
Smith, L. (1993). Necessary knowledge: Piagetian perspectives on constructivism. Hillsdale, NJ: Erbaum. [ Links ]
Smith, L. (Ed.). (1996). Critical readings on Piaget. London: Routledge. [ Links ]
Smith, L. (1997). Necessary knowledge and its assessment in intellectual development. In L. Smith, J. Dockrell, & P. Tomlinson (Eds.), Piaget, Vygotsky and beyond (pp. 224-241). London: Routledge. [ Links ]
Smith, L. (2009). Piaget’s developmental epistemology. In U. Müller, J. Carpendale, & L. Smith (Eds.), The British companion to Piaget (pp. 64-93). Cambridge: Cambridge University Press.
Turiel, E. (1983). The development of social knowledge: Morality and convention. Cambridge: Cambridge University Press. [ Links ]
Zelazo, P., Chandler, M., & Crone, E. (Eds.). (2010). Developmental social cognitive neuroscience. New York & London: Psychology Press. [ Links ]
Correspondence concerning this article should be addressed to: Orlando M. Lourenço, Departamento de Psicologia, Faculdade de Psicologia, Universidade de Lisboa, Alameda da Universidade, 1649-013 Lisboa, Portugal. E-mail: oml2105@fp.ul.pt
We wish to thank all the children for their participation in this study. We would also like to thank the schools where the children were enrolled. The author expresses his gratitude to Jorge Martins and Mariana Coelho for their help with data collecting, and thanks Armando Ferreira for his help with the statistical analyses reported in this study.
We would like to thank Andreas Demetriou for his helpful comments on an earlier version of this paper, and his help with the English.
Submitted: 18/04/2018 Accepted: 14/06/2019