Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Silva Lusitana
versão impressa ISSN 0870-6352
Silva Lus. v.17 n.2 Lisboa dez. 2009
Caracterização da Estrutura e Dinâmica das Populações de Lince Ibérico (Lynx pardinus)
Uma Digressão Exploratória
Luís Soares Barreto
Professor Catedrático Jubilado
Av. do Movimento das Forças Armadas, 41-3D, 2825-372 COSTA DA CAPARICA
Sumário. Recorrendo a dados obtidos na meta população de lince ibérico (Lynx pardinus, Temminck) do sudoeste de Espanha e à sua teoria matematizada para as populações, o autor estabelece os parâmetros característicos da espécie e tipifica a sua estratégia bionómica. Estabelece modelos matriciais de idade e de estádios e pela via analítica e simulatória aborda o comportamento das populações sujeitas a estocacidade demográfica e/ou ambiental, e o equilíbrio da territorialidade.
Palavras-chave: Análise da viabilidade; lince ibérico; estocacidade demográfica e ambiental
An Inquiry on the Structure and Dynamics of the Populations of Iberian Lynx (Lynx pardinus)
Abstract. The author uses data obtained in Spain from a metapopulation of Lynx pardinus, and his unified theory for populations to characterize the structure, and dynamics of the pristine populations of this lynx. He considers situations of demographic and environmental stochasticity, the equilibrium of the territoriality, and population viability analysis.
Key words: Demographic and environmental stochasticity; Iberian lynx; population viability analysis
L'Analyse et Simulation des Populations de Lynx Ibérique (Lynx pardinus)
Résumé. L'auteur utilise l'information obtenue d'une métapopulation de Lynx pardinus, située en Espagne et sa théorie unifiée des populations pour caractériser la structure et la dynamique des populations primitives du félin, son comportement sujet à la stochasticité démographique et de l'environnement. Il analyse la viabilité de la population.
Mots clés: Analyse de la viabilité; lynx ibérique; stochasticité démographique et de l'environnement
Introdução
Actualmente, o lince ibérico (Lynx pardinus, Temminck; LI) é uma espécie com elevado risco de extinção, a viver em remanescentes e pequenas manchas do seu habitat, em reduzidas populações locais, interligadas (meta populações) ou não. Esta situação torna quase impossível estudar-se e caracterizar-se populações de LI, em condições prístinas.
A única via para ultrapassar esta lacuna, é recorrer à informação obtenível nas condições actuais, e utilizar uma estrutura teórica para estabelecer prováveis estimativas da estrutura, dinâmica e viabilidade intrínseca das populações de LI, em seus habitats não alterados. Hipoteticamente, isto fornece informação passível de maior generalização e mais abrangente aplicabilidade, sempre necessária em trabalhos de preservação, expansão e eventuais repovoamentos com a espécie, ou mesmo que seja só para fins comparativos.
Neste enquadramento, este texto é uma aplicação da minha teoria para a estrutura e dinâmica das populações (Barreto, 2005: Parte I) à informação sobre a demografia do LI a que tive acesso e se concentra em Gaona, Ferreras e Delibes (1998). Estes três autores estudam a meta população de LI existente no sudoeste de Espanha, e aqui compilam e introduzem dados, não só preciosos mas também provavelmente únicos, a que recorro.
Desenvolvo um esforço no sentido de a) procurar estabelecer os parâmetros característicos da espécie; b) discernir a sua estratégia bionómica; c) pela via analítica e simulatória, avaliar a sua viabilidade ou inerente susceptibilidade à extinção. A abordagem empreendida é genérica, não pressupõe a fragmentação do habitat, ou constrições devido a sua excessiva exiguidade, mas, presumidamente, o LI a viver em condições prístinas, ou, pelo menos, próximo delas.
Como é usual em análise demográfica, considero uma população só de fêmeas, com ninhadas em que a razão dos sexos é 1:1 (Gaona, et al., 1998:351). Grande parte da informação utilizada respiguei-a do Quadro 3 dos mesmos autores (Gaona, et al., 1998:355).
Um breve e único comentário sobre o LI em Portugal. O assunto é controverso, e não me é possível fazer qualquer contribuição meritória para a polémica acerca da sua ausência ou presença. O repovoamento com a espécie depende de se vir a dispor de exemplares para o efeito e habitat adequado com área suficiente, protegido de qualquer futura destruição e fragmentação. Como o LI é predador de espécies cinegéticas, nomeadamente o coelho bravo (Oryctolagus cuniculus) a sua eventual e futura existência, em populações viáveis, não será vista com igual simpatia por todos.
A estrutura do texto esquematiza-se na Figura 17, cujo visionamento pode ser, eventualmente, do interesse do leitor antecipar.
Na preparação deste estudo, recorri ao software Scilab para o cálculo numérico, e ao R para ajustar as regressões apresentadas.
Demografia I: um modelo matricial de estrutura etária
Recorrendo aos valores apresentados por (Gaona, et al., 1998), proponho o modelo matricial de estrutura etária, para as fêmeas do LI, inserto no Quadro 1 (Barreto, 2005: caps. 6 e 7). Assume: a) que a população está em equilíbrio dimensional, isto é, atingiu o seu tamanho constante (valor próprio dominante (λ) igual a 1,0000); b) a estrutura etária estável; c) as condições óptimas em que todas as fêmeas em idade reprodutiva têm acesso a um território.
Quadro 1 - Modelo matricial de estrutura etária (anual) para fêmeas do LI. Matriz A1
| 0 | 0 | 0,2587 | 0,6 | 0,9 | 0,9 | 0,9 | 0,9 | 0,32 | 0,3 | 0 | 0 | 0 |
| 0,4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
A análise desta matriz permite obter a informação sobre a população (e. g., Caswell, 2001:90-94) inserta no Quadro 2.
Quadro 2 - Estrutura etária estável (EEE) e valores reprodutivos (VR) das idades, associada ao modelo do Quadro 1
| EEE | VR |
| 0,3273 | 1 |
| 0,1309 | 2,5000 |
| 0,0916 | 3,5714 |
| 0,0825 | 3,6808 |
| 0,0742 | 3,4231 |
| 0,0668 | 2,8035 |
| 0,0601 | 2,1150 |
| 0,0541 | 1,3500 |
| 0,0487 | 0,5000 |
| 0,0292 | 0,3000 |
| 0,0175 | 0 |
| 0,0105 | 0 |
| 0,0063 | 0 |
Na Figura 1, recorrendo à matriz A1, apresento a dinâmica de uma população que se inicia com 100 indivíduos recém nascidos. Estabiliza com 51 fêmeas, assim distribuídas pelas idades: 17; 7; 5; 4; 4; 3; 3; 3; 2; 1; 1; 1; 0.
Figura 1 - Dinâmica de uma população que se inicia com 100 recém nascidos, projectada com a matriz A1
No Quadro 3, insiro a análise da sensibilidade do valor próprio dominante (a taxa finita de crescimento da população) λ.
Quadro 3 - Análise da sensibilidade do valor próprio dominante da matriz A1, λ=1. Matriz S1
| 0,167 | 0,067 | 0,047 | 0,042 | 0,038 | 0,034 | 0,031 | 0,028 | 0,025 | 0,015 | 0,009 | 0,005 | 0,003! |
| 0,417 | 0,167 | 0,117 | 0,105 | 0,095 | 0,085 | 0,077 | 0,069 | 0,062 | 0,037 | 0,022 | 0,013 | 0,008 |
| 0,596 | 0,238 | 0,167 | 0,150 | 0,135 | 0,122 | 0,110 | 0,099 | 0,089 | 0,053 | 0,032 | 0,019 | 0,011 |
| 0,614 | 0,246 | 0,172 | 0,155 | 0,139 | 0,125 | 0,113 | 0,102 | 0,091 | 0,055 | 0,033 | 0,020 | 0,012 |
| 0,571 | 0,229 | 0,160 | 0,144 | 0,130 | 0,117 | 0,105 | 0,094 | 0,085 | 0,051 | 0,031 | 0,018 | 0,011 |
| 0,468 | 0,187 | 0,131 | 0,118 | 0,106 | 0,095 | 0,086 | 0,077 | 0,070 | 0,042 | 0,025 | 0,015 | 0,009 |
| 0,353 | 0,141 | 0,099 | 0,089 | 0,080 | 0,072 | 0,065 | 0,058 | 0,052 | 0,032 | 0,019 | 0,011 | 0,007 |
| 0,225 | 0,090 | 0,063 | 0,057 | 0,051 | 0,046 | 0,041 | 0,037 | 0,033 | 0,020 | 0,012 | 0,007 | 0,004 |
| 0,083 | 0,033 | 0,023 | 0,021 | 0,019 | 0,017 | 0,015 | 0,014 | 0,012 | 0,007 | 0,004 | 0,003 | 0,002 |
| 0,05 | 0,020 | 0,014 | 0,013 | 0,011 | 0,010 | 0,009 | 0,008 | 0,007 | 0,004 | 0,003 | 0,002 | 0,001 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
A matriz S1 é típica dos estrategas K (Barreto, 2005: cap. 9). A maior sensibilidade está associada à sobrevivência das recém nascidas (S1(2,1)), isto é, à ultrapassagem do primeiro ano de vida. No quadro 4, insiro os valores de λ associados a matrizes idênticas à A1, em que o valor de A1(2,1) foi substituído por 0,1, 0,2,...0,7.
Quadro 4 - Valores de λ para vários valores da taxa de sobrevivência dos recém nascidos
| A1(2,1) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| λ | 0,8034 | 0,8936 | 0,9536 | 1,0000 | 1,0383 | 1,0713 | 1,1005 |
Recorrendo a Barreto (2005:cap. 8), da matriz S1 é possível obter os seguintes índices:
de crescimento: 0,5844; de regeneração: 0,2712; de sobrevivência: 0,7287.
Demografia II: os parâmetros característicos da população do LI
Escreva-se a equação de Gompertz na forma:
yi = yif Riexp(-ct) (1)
A matriz A1 permite obter as razões "valor inicial/valor final" (Ri) das variáveis individuais e populacionais do LI (Barreto, 2005: capítulos 1 a 4) e valor do chamado coeficiente de competição (c), na equação de Gompertz, como se exibe no Quadro 5.
Quadro 5 - Parâmetros característicos da dinâmica individual e populacional do LI
| c | R-2 | R1 | R2 | R2,67 | R3 | R4,67 |
| 0,3920 | 9,7730 | 0,3199 | 0,1023 | 0,0478 | 0,0327 | 0,0049 |
Os valores de R-2 e c permitem estabelecer o valor da taxa líquida de reprodução (Ro) estimada em 2,2435 fêmeas/fêmea/longevidade e a duração média de uma geração: 4,4 anos.
Recorrendo aos mesmos parâmetros, proponho a tabela de vida para as fêmeas de LI, inserta no quadro 6.
Quadro 6 - Tabela de vida para uma população de LI em equilíbrio dimensional e estrutural. X=idade; lx=número de sobreviventes; timia=taxa instantânea de mortalidade no início do ano; tms=taxa média de sobrevivência; tmm=taxa média de mortalidade; e=esperança de vida
| x | lx | timia | nm | tms | tmm | e |
| 0 | 100 | 0,8936 | 52 | 0,4775 | 0,5225 | 2,7582 |
| 1 | 48 | 0,6038 | 19 | 0,6068 | 0,3932 | 4,3195 |
| 2 | 29 | 0,4080 | 8 | 0,7135 | 0,2865 | 5,8383 |
| 3 | 21 | 0,2757 | 5 | 0,7961 | 0,2039 | 7,0043 |
| 4 | 16 | 0,1863 | 2 | 0,8572 | 0,1428 | 7,6832 |
| 5 | 14 | 0,1259 | 1 | 0,9011 | 0,0989 | 7,8874 |
| 6 | 13 | 0,0850 | 1 | 0,9320 | 0,0679 | 7,7025 |
| 7 | 12 | 0,0575 | 1 | 0,9536 | 0,0464 | 7,2303 |
| 8 | 11 | 0,0388 | 0 | 0,9684 | 0,0316 | 6,5598 |
| 9 | 11 | 0,0262 | 0 | 0,9785 | 0,0215 | 5,7587 |
| 10 | 11 | 0,0177 | 1 | 0,9854 | 0,0146 | 4,8749 |
| 11 | 10 | 0,0120 | 0 | 0,9901 | 0,0099 | 3,9400 |
| 12 | 10 | 0,0081 | 0 | 0,9933 | 0,0067 | 2,9746 |
| 13 | 10 | 0,0055 | 0 | 0,9955 | 0,0045 | 0 |
Na Figura 2, simulo o crescimento da biomassa de um lince que atinge no estado adulto 12 quilogramas.

Figura 2 - Dinâmica da biomassa de um LI
Na Figura 3, simulo a curva de sobrevivência do LI.
Figura 3 - Curva de sobrevivência de uma corte de LI
Modelo matricial de estádios
Os modelos matriciais de estrutura etária podem ser considerados um caso particular dos modelos matriciais de estádios, em que indivíduos de mais de uma idade são agrupados de acordo com as fases da biologia da espécie. Frequentemente, a facilidade de manipulação e predicabilidade destes últimos modelos é superior aos da estrutura etária.
Nesta secção, introduzo um modelo matricial de estádios para o LI, retendo os outros pressupostos do modelo A1. Estabeleço quatro fases na sua biologia: estádio 1: recrutamento, compreendendo os indivíduos desde o nascimento até atingirem o primeiro ano de vida; estádio 2: juvenil, de 1 até aos 2 anos; estádio 3: reprodutivo: dos 2 aos 9 anos; estádio 4: pós reprodutivo: a fase terminal da vida até ao limite da longevidade (13 anos). O modelo conceptual é graficamente representado na Figura 4, e descrito pela matriz A2, no Quadro 7. Considero projecções anuais.
Figura 4 - Diagrama do modelo matricial de estádios do LI
Quadro 7 - Modelo matricial de estádio (anual) para fêmeas do LI. Matriz A2
| 0 | 0 | 0,87 | 0 |
| 0,4 | 0 | 0 | 0 |
| 0 | 0,7 | 0,8104 | 0 |
| 0 | 0 | 0,0861 | 0,2466 |
A sensibilidade de λ insere-se no Quadro 8. A maior sensibilidade está associada à fracção dos indivíduos que permanecem na fase reprodutiva, no ano.
Quadro 8 - Análise da sensibilidade do valor próprio dominante da matriz A2, λ=1,037. Matriz S2
| 0,1520 | 0,0586 | 0,1812 | 0,0197 |
| 0,3941 | 0,1520 | 0,4698 | 0,0512 |
| 0,5839 | 0,2252 | 0,6959 | 0,0758 |
| 0 | 0 | 0 | 0 |
A maior sensibilidade de λ está agora associada à permanência das fêmeas no estádio reprodutivo.
Quadro 9 - Estrutura etária estável (EEE) e valores reprodutivos (VR) das idades, associada ao modelo do quadro 7
| EEE | VR |
| 0,3693 | 1 |
| 0,1424 | 2,5924 |
| 0,4402 | 3,8402 |
| 0,0479 | 0 |
Da matriz A2 é possível extrair a cadeia de Markov do Quadro 10, onde se destaca a cheio a sub matriz de transição T.
Quadro 10 - Cadeia de Markov associada à matriz A2. Matriz M1
| 0 | 0 | 0 | 0 | 0 |
| 0,4 | 0 | 0 | 0 | 0 |
| 0 | 0,7 | 0,8104 | 0 | 0 |
| 0 | 0 | 0,0861 | 0,2466 | 0 |
| 0,6 | 0,7 | 0,1035 | 0,7534 | 1 |
A matriz T permite obter a informação do Quadro 11 (e. g., Caswell, 2001:119).
Quadro 11 - Parâmetros da dinâmica do modelo de estádios A2. medest= tempo médio de permanência no estádio; var1= variância de medest; espest = esperança de vida do estádio; var 2=variância de espest; Ro = taxa líquida de reprodução do estádio
| Estádios | medes | var1 | espest | var2 | Ro |
| 1 | 1 | 0 | 3,0 | 15,7 | 1,2848 |
| 2 | 1 | 0 | 5,1 | 23,5 | 3,2120 |
| 3 | 5,3 | 22,5 | 5,9 | 23,2 | 4,588 |
| 4 | 1,3 | 0,4 | 1,3 | 0,4 | 0 |
O valor médio de Ro, no quadro 11, é 2,2714, próximo do anteriormente encontrado (2,2435).
Estocacidade demográfica: abordagem simulatória
Uma equação diferencial escolástica de Ito
Uma equação diferencial para o modelo de Gompertz (eq.(1)) é a seguinte:
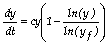 (2)
(2)
Criemos um processo estocástico de nascimento e morte, assumindo Y(t) como uma variável aleatória do tamanho da população. Num pequeno intervalo de tempo Δt, seja a probabilidade de um nascimento igual a cY(t)Δt e a de uma morte a cYln(Y)/ln(Yf)Δt. Então a equação diferencial estocástica para o crescimento gompertziano satisfaz a relação seguinte:
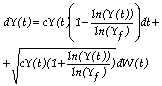 (3)
(3)
podendo tomar Y(t) valores iguais ou superiores a zero. W representa um processo de Wiener.
Aplicando o método de Euler à eq. (3), obtenho a equação recorrente seguinte:
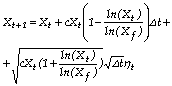 (4)
(4)
em que ηt~N(0,1).
Na Figura 5, apresento três simulações da variação de uma população de LI, que já tenha atingido a capacidade de sustentação yf (=10), durante dez anos.
Figura 5 - Simulação estocástica do tamanho de uma população de LI, depois de ter atingido a capacidade de sustentação (10 indivíduos), durante dez anos, recorrendo à eq. (4). Δt=0,01
Para elaborar esta subsecção recorri a Allen (2003).
Modelo matricial
O LI sendo uma espécie com elevado risco de extinção, confinado a pequenas populações, não é imune ao efeito da estocacidade demográfica, pelo que se justifica uma indagação simulatória e analítica nesta área, embora se presuma que fosse pouco relevante, na generalidade, para o LI nas condições primevas. Nesta secção explano a abordagem simulatória.
Para simular o crescimento de uma população de LI sujeita a estocacidade demográfica, recorro a duas matrizes. A primeira é obtida da cadeia de Markov eliminando a última coluna da direita (coluna 4) e designo-a por C. A segunda é obtida da matriz A2, fazendo iguais a zero os elementos das linhas 2 a 4. Será a matriz F. Estas duas matrizes serão sujeitas a estocacidade seguindo o procedimento descrito em Caswell (2001:458-459). A matriz C é simulada recorrendo a uma distribuição multinomial, e a F a uma de Poisson. Considero 10 combinações de F(1,3) e C(2,1). Considerei populações iniciais de uma fêmea em cada estádio. Para cada uma delas simulei 20 conjuntos de 1000 simulações com a duração de 100 anos e obtive, para cada uma a média da sobrevivência percentual e coeficiente de variação associado, conforme exibo no Quadro 12.
Quadro 12 - Sobrevivência percentual média, em 100 anos, de uma população inicial de LI com uma fêmea em cada estádio, em várias condições de fertilidade (F(1,3)) e sobrevivência das recém nascidas (C(2,1)). PMS = percentagem média de sobrevivência até aos 100 anos; CV = coeficiente de variação
| Conjunto | F(1,3) | C(2,1) | P M S | CV | λ |
| 1 | 0,47 | 0,4 | 0,58 | 46,67 | 0,955 |
| 2 | 0,47 | 0,5 | 5,1 | 11,15 | 0,981 |
| 3 | 0,57 | 0,4 | 3,5 | 14,44 | 0,977 |
| 4 | 0,57 | 0,5 | 19,4 | 6,71 | 1,007 |
| 5 | 0,6772 | 0,4 | 13,6 | 8,05 | 1,000 |
| 6 | 0,6772 | 0,5 | 39,7 | 4,51 | 1,033 |
| 7 | 0,77 | 0,4 | 27,66 | 4,57 | 1,018 |
| 8 | 0,77 | 0,5 | 53,6 | 3,06 | 1,053 |
| 9 | 0,87 | 0,4 | 42,4 | 3,91 | 1,037 |
| 10 | 0,87 | 0,5 | 63,7 | 2,49 | 1,074 |
Os valores de PMS e λ permitiram-me ajustar a seguinte regressão:
PMS=67989,83–200389λ+196198,1λ2-63784,3λ3
(R2aj = 0,999; F = 4017,02; p=0,0000 ) (5)
Embora a eq. (5) seja um modelo empírico que não acresce inteligibilidade ao assunto em análise, na Figura 6, exibo os 10 pares de valores do quadro 12, e os obtidos com ela. São virtualmente coincidentes.
Figura 6 - Valores da percentagem média de sobrevivência até aos 100 anos (PMS) obtidos por simulação e gerados pela eq. (5)
Na Figura 7, exibo duas simulações, nas condições do conjunto 9, do Quadro 12.
Figura 7 - Duas simulações de uma população inicial de uma fêmea em cada estádio, sujeita a estocacidade demográfica, durante 100 anos. F(1,3)=0,87 e C(2,1)=0,4
Estocacidade demográfica: abordagem analítica
Um tratamento mais preciso que o simulatório, da estocacidade demográfica, pode ser levado a cabo analiticamente, recorrendo aos processos de ramificação ou arborescentes ("branching processes"), cuja aplicação só recentemente vem ganhando interesse em ecologia (Kimmel e Axelrod, 2002; Caswell, 2001:cap. 15).
Os processos de ramificação surgiram da procura de solução para o problema de avaliar a probabilidade extinção das linhagens aristocráticas britânicas, no século XIX. Foi neste contexto que surgiu o processo de ramificação de Galton-Watson, o mais antigo e simples, sendo a ele que nesta secção recorro.
A aplicação mais recente dos processos de ramificação estende-se a diversos domínios da biologia molecular. Para este domínio de aplicação veja-se Kimmel e Axelrod (2002).
Esta abordagem descreve um grupo de organismos (o nosso caso particular) que dão origem, casualmente e de acordo a certas regras probabilísticas, a outros organismos, que por sua vez também proliferam, gerando-se, a partir de cada um, uma árvore de descendência, e daqui a designação de processo de ramificação ou arborescente.
Restrinjo a aplicação do processo à avaliação das probabilidades de extinção das linhagens de cada estádio, seguindo de perto Caswell (2001:493-497).
Na Figura 8, insiro a evolução das probabilidades de extinção de cada estádio até se atingirem valores estáveis, para o caso de uma população crescendo de acordo com a matriz A2. As probabilidades de extinção estimadas são as seguintes:
Estádio 1: 0,9722; estádio 2: 0,9331; estádio 3: 0,9059; estádio 4: 0,9981.
Uma população muito pequena, com estas probabilidades de extinção, só pode ser salva por estocacidade ambiental favorável ou imigração.
Figura 8 - Probabilidades de extinção dos estádios da população de fêmeas de LI, sujeitas à dinâmica da matriz A2. O estádio 4 pode-se dizer que tem extinção garantida
Quadro 13 - Probabilidades de extinção dos estádios da população de fêmeas de LI, para os valores extremos da Figura 9, da sobrevivência das recém nascidas
| Estádios | A2(2,1)=0,30 | A2(2,1)=0,70 |
| 1 | 0,9924855 | 0,7626770 |
| 2 | 0,9782850 | 0,6623957 |
| 3 | 0,9704071 | 0,5191367 |
| 4 | 0,9981418 | 0,9981418 |
Para vários valores de A2(2,1), taxa de sobrevivência das recém nascidas, estimei as probabilidades de extinção dos estádios de acordo com o exibido na Figura 9. A influência do valor da taxa de sobrevivência das recém nascidas aumenta a partir da taxa 0,4, melhorando conspicuamente a probabilidade das linhagens dos estádios 1, 2 e 3 não se extinguirem. A probabilidade de extinção do estádio 4 é praticamente insensível a variação da mesma taxa.
Figura 9 - Probabilidades de extinção dos estádios da população de fêmeas de LI, para vários valores da taxa de sobrevivência das recém nascidas (s)
Estocacidade ambiental
Nesta secção, vou elaborar duas aproximações ao seu tema. Uma genérica e mais facilmente calculável, e outra recorrendo à matriz A2 (quadro 7).
Na primeira abordagem, recorro ao modelo de Goodman (1993:13), modificado para mais expedita computação (Belovsky, 1993:37). Este modelo fornece estimativas do tempo de persistência médio de uma população T, de que se conheça a taxa intrínseca de crescimento natural r, a sua variância induzida pela estocacidade ambiental v, e a capacidade de sustentação do local para a população K.
Para duas populações com o mesmo valor de K ou yf, uma crescendo de acordo com a curva logística e outra segundo a de Gompertz, verifica-se a seguinte relação (Elseth e Baumgardner, 1981: 270):
r= c ln K (6)
Para discernir os efeitos da capacidade de sustentação e da variância de r, no tempo de persistência médio de uma população de LI, recorri ao modelo modificado de Goodman, utilizando a eq. (6).
No Quadro 14, exibo os resultados da aplicação das equações propostas por Belovsky, procurando cobrir tanto situações de fragmentação do habitat como primevas.
Quadro 14 - Tempos de persistência (T, anos) associados à maior variância de r (v) suportada pela população, quando ocorre uma dada capacidade de sustentação (K). Para maiores valores de v a população extingue-se
| K | 2 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 500 | 1000 |
| T | 8 | 77 | 112 | 146 | 177 | 207 | 235 | 264 | 292 | 319 | 346 | 1266 | 2274 |
| v | 0,299 | 0,993 | 1,291 | 1,446 | 1,591 | 1,687 | 1,765 | 1,832 | 1,889 | 1,940 | 1,985 | 2,680 | 2,979 |
Quanto menor for K, mais susceptível é a população à extinção, e menos tolerante é à variância de r, o que era esperado. Para K≥10, a relação entre K e T é virtualmente linear, como comprova a eq. (7).
T=90,60558+2,21109 K (7)
(R2aj=0,998, F=4596, p=0,0000)
Os valores de v, exibidos no Quadro 14 implicam a razão v/r=1,1. Comparando com a amplitude de valores mencionada Belovsky (1993:54), em que o mínimo referido desta razão é 1,43, este valor é muito baixo, o que confirma a fragilidade da persistência da espécie.
Outra possibilidade passa pelo recurso à simulação com a matriz A2 modificada. Considero os efeitos simultâneos da estocacidade ambiental e da densidade. Para isso: a) faço s1 ser uma variável com distribuição normal de média 0,4 e variância 1; a classe 3 é decomposta em duas, uma cujas fêmeas não ocupam território mas têm possibilidade de ter acesso aos que possam deixar de estar ocupados (3A) e outra cujos membros dispõem de território e reproduzem-se (3B). O novo diagrama da estrutura da população insere-se na Figura 10.

Figura 10 - Representação diagramática da população associada à matriz A2, considerando fêmeas reprodutivas dispondo (3B) ou não (3A) de território
Não disponho de dados da variação ambiental associados ao estudo de qualquer população de LI, por isso, arbitrariamente e só com propósitos ilustrativos, como já disse, considero só o efeito da variação ambiental sobre s1 (sensibilidade de λ=0,3941, quadro 8), à semelhança dos autores espanhóis, assumindo, s1=N(0,4, 1).
Na Figura 11, simulo o efeito do número de territórios na probabilidade de quase extinção. O efeito é conspícuo.
Figura 11 - Três simulações do efeito do número de territórios disponíveis na probabilidade de extinção, no período de 50 anos, com uma população inicial de [4 2 4 3 2] e s1=N(0,4, 1). Para cada valor de territórios disponíveis foram feitas 1000 simulações. A população considera-se extinta (inviável) quando o número de indivíduos é inferior a três
Se considerar só s3=N(0,81, 2), a sensibilidade de λ relativamente a esta variável é 0,6959, a maior, verifica-se a elevada probabilidade da população ser inviável para os números de territórios considerados (≤10).
Estocacidades ambiental e demográfica
Em benefício da completude da exposição, importa apresentar um modelo que abarque, simultaneamente as estocacidades ambiental e demográfica. O modelo que proponho é o seguinte (Barreto, 2005:31, eq.(4.54); Lande et al., 2003:110):
yt+1 = yt + yt (c log(yf/yt) + εt) (8)
y = número de fêmeas; c = 0,392, anteriormente estimado; εt = N(0, σ2), em que
σ2 = σ2a + σ2d /y (9)
σ2a = variância ambiental; σ2d = variância demográfica.
Importa anotar que a variância demográfica para a população só de fêmeas é inferior à da população total, abarcando fêmeas e machos (Lande et al., 2003:11). Para tamanhos da população tais que y> 10 σ2d/ σ2a a estocacidade demográfica pode ser ignorada (Lande et al., 2003:9).
Em Barreto (2005:31) analiso a estabilidade da eq. (8).
Não disponho de valores das duas variâncias, para qualquer população do LI, por isso a título meramente ilustrativo, apresento o gráfico da Figura 12, assumindo, arbitrariamente, σ2a =0,1 e σ2d=0,15, para valores de yf =10, 30 e 50 e a população inicial de uma fêmea.
Figura 12 - Projecções estocásticas de populações de fêmeas de LI, recorrendo à eq. (9). σ2a =0,1 e σ2d=0,15; yf =10, 30 e 50, sendo a população inicial de uma fêmea. Três grupos de quatro simulações
Uma alternativa à eq. (8) é a seguinte:
yt+1 = yt (exp(c ln(yf)-c ln(yt)) + εt) (10)
Na Figura 13, exibo as diferença "eq.(8)-eq.(10)", para os mesmos valores de εt. As maiores diferenças ocorrem nos primeiros anos, e com os maiores valores de yf. Verifica-se "eq.(8)<eq.(10)".
Figura 13 - Diferenças entre os valores dados pelas eqs. (8) e (10), para os mesmos valores de εt. yf=10, 30 e 50
Na análise da viabilidade de uma população, as curvas da probabilidade acumulada de extinção, para um período de tempo seleccionado, para vários valores, por exemplo, da capacidade de sustentação, são instrumentos valiosos (e.g., Morris e Doak, 2002:45). Recorrendo à simulação, a eq. (11) pode ser utilizada para estabelecer estas curvas, como ilustro na Figura 14.
Figura 14 - Probabilidades acumuladas de extinção, pelo período de cinquenta anos, de uma população inicial de uma fêmea de LI, para valores de yf de 1 a 10, sendo σ2a =0,3 e σ2d=0,45. Para cada valor de yf foram realizadas 5000 simulações
O Equilíbrio da territorialidade
O LI exibe territorialidade intra sexual (Gaona et al., 1998:351) pelo que se justifica não ignorar este aspecto. O meu propósito é estabelecer a proporção dos territórios disponíveis numa vasta área, que são ocupados pelas fêmeas de LI (p), numa situação de equilíbrio da população (λ=1).
A minha fonte nesta secção é Lande, Engen e Sæther (2003:80-84), utilizando o modelo estabelecido em 1987, pelo primeiro autor, que é explanado e deduzido neste livro.
Nesta inquirição, considerarei duas situações: a) não há dificuldade no acasalamento; b) os machos são escassos. Presumo que a primeira situação deveria prevalecer nas populações prístinas de LI. Abordo a segunda por ser a verificada no sudoeste de Espanha, e ser tida como a principal limitação ao crescimento de algumas populações da meta população ali existente e estudada (Gaona et al., 1998:361).
A situação de abundância de machos
Passo a descrever o modelo de Lande aplicável neste contexto.
A taxa de ocupação dos territórios disponíveis p, pode assumir dois valores;
p=1-(1-k)/h se h>1-k (11a)
p=0 se h≤1-k (11b)
k=(1-1/Ro)1/m (11c)
sendo h a proporção da área que é de facto utilizável pela espécie; m é o número máximo de territórios que uma jovem fêmea pode procurar antes de morrer, sem encontrar nenhum que possa ocupar. Este parâmetro deve variar com as condições locais de ocupação e dispersão dos territórios. Ro, a taxa líquida de reprodução, já foi anteriormente estimada em 2,2435.
Verifica-se aqui a ocorrência de um mecanismo de efeito da Allee, pois para valores de h iguais e menores que um limiar crítico h*, a população extingue-se.
Nas minhas simulações com este modelo assumi valores de h de 0,3 a 1, e valores de m=5, 10, 15, 20. Os valores h* associados a m inserem-se no Quadro 15.
Quadro 15 - Valores de h* tais que h ≤ h* implica a extinção da população
| m | 5 | 10 | 15 | 20 |
| h* | 0,111 | 0,057 | 0,038 | 0,028 |
Exibo na Figura 15 o resultado das simulações. Como era de esperar, maiores valores de m e h proporcionam populações maiores, em equilíbrio.
Figura 15 - Valores da proporção de territórios ocupados, na situação de equilíbrio (p*), para m=5, 10, 15, 20 (curvas de baixo para cima), quando não há dificuldade de acasalamento (eq. (11))
Situação de escassez de machos
O modelo de Lande assume agora a forma da equação 12, que só pode ser resolvida numericamente:
[1-(1-h-hp)m] [1-(1-(1-p) (1-hp)n]Ro=1 (12)
onde n é o número de territórios vizinhos aos de uma fêmea onde ela procura encontrar um macho para acasalamento.
Na Figura 16, apresento simulações efectuadas com o modelo da eq. (12), assumindo n=5 e 10.
Figura 16 - Valores da proporção de territórios ocupados, na situação de equilíbrio (p*), para m=5, 10, 15, 20 (curvas de cima para baixo), quando há dificuldade de acasalamento (eq. (12)). n=10 (gráfico superior) e n=5
É conspícuo que a falta de machos tem um marcado efeito no valor de p* e pode, de facto, levar à extinção de uma população se não ocorrer a imigração de animais provenientes de outros locais, como acontece em Espanha.
Comentários conclusivos
Antes de prosseguir, gostaria que o leitor tivesse presente os propósitos deste artigo, exarados na introdução, para melhor contextuação do que se segue.
Em benefício da organização, mais conspícua articulação e inteligibilidade destas considerações conclusivas, exibo o esquema da estrutura do texto, na Figura 17.
Figura 17 - Descrição diagramática da estrutura do artigo
Como nela se confirma, tudo começa com os dados de Gaona et al. (1998). Em verdade, não estou em posição de poder comentar, com objectividade e interesse, os dados destes autores, para além da asserção genérica que reconhece não haver dados que estejam completamente expurgados de erro. Limito-me a lembrar que a amostragem de populações com muito poucos indivíduos (raras) é extremamente difícil e mais sujeita a erros que a de populações mais numerosas. É pois evidente e trivial que a qualidade dos resultados das minhas elaborações, por muita correcção teórica, lógica e dedutiva que estas eventualmente tenham, é fundamentalmente afectada pelo nível de exactidão da informação sobre a biologia e ecologia do LI, a que recorro. Esta utilização tem implícito que assumo ser a sua correcção suficiente para os meus propósitos. Sobre dados é tudo o que tenho por curial dizer.
As questões que agora surgem são duas, e dizem respeito a) à correcção com que integrei os dados a que recorri nos modelos da minha teoria, b) a objectividade ou adequação externa (à realidade de que se ocupa) da mesma teoria.
No que respeita à qualidade da minha teoria, não a vou discutir aqui, por ser deslocado, e remeto o leitor para os comentários e análise que a ela faço em Barreto (2005), para além dos juízos que sobre ela cada um possa fazer. Limito-me a dizer que não conheço outra tão abrangente e, simultaneamente, de tão elevada coerência interna.
O modelo de cuja correcção praticamente tudo depende é a matriz de Leslie (A1), exibida no Quadro 1. Dispondo-se de dados fiáveis para o efeito, a construção desta matriz não levanta grande dificuldade e por isso deverá ser altamente provável que o seu nível de inexactidão a não torne totalmente desinteressante, e condenada a ser ignorada.
Posto isto, não repugna admitir que os valores estimados dos parâmetros característicos da espécie também possam ter nível de verosimilitude que os façam merecedores de aceitação, certamente sempre transitória (trata-se ciência), até se alcançarem outros mais precisos.
São alguns dos parâmetros atrás mencionados (c, Ro e R-2) que permitem as análises e simulações subsequentes. Estas dependem não só do trabalho desenvolvido por mim até então, mas também dos instrumentos a que recorri tanto do edifício da modelação e análise matricial das populações, como de alguns modelos propostos por outros autores, devidamente identificados, e tidos como adequados para o meu labor exploratório, no âmbito da ecologia das populações de LI. Deixo ao juízo do leitor avaliar da justeza das minhas opções pois, obviamente, tenho-as como curiais e defensáveis.
Dada a natureza exploratória e genérica deste estudo (não abordei o caso de uma qualquer população com existência real) omiti estimativas de intervalos de confiança.
Em meu entendimento, duas evidências da maior relevância emergem do texto: a) a muito provável fragilidade da sobrevivência das populações do LI, inerente às suas características e b) a vantagem de se dispor de uma teoria integrada, para poder dar amplo aproveitamento a informação restrita, que doutra maneira seria de pouca utilidade e requereria muito mais tempo e recursos para ser completada. É a capacidade integradora e de descoberta das teorias que permite a Feynman (1989:45) escrever: "A Natureza utiliza longos fios mas os bocados mais pequenos permitem revelar a estrutura de toda a tapeçaria".
Bibliografia
Allen, L.J.S., 2003. An Introduction to Stochastic Processes with Applications to Biology. Pearson Education, Inc., Upper Saddle River, New Jersey.
Barreto, L.S., 2005. Theoretical Ecology. A Unified Approach. Edição do Autor, Lisboa. Divulgado em CD.
Belovsky, G.E., 1993. Extinction Models and Mammalian Persistence. Em M. E. Soulé Viable Populations for Conservation, Cambridge University Press, Cambridge, pp. 35-57.
Caswell, H., 2001. Matrix Population Models. Construction, Analysis, and Interpretation. Sinauer Associates, Inc. Publishers, Sunderland, MA.
Elseth, G.D., Baumgardner, K.D., 1981. Population Biology. D. Van Nostrand, New York.
Gaona, P., Ferreras, P., Delibes, M., 1998. Dynamics and Viability of a Metapopulation of the Endangered Iberian Lynx (Lynx pardinus). Ecological Monographs 68(3): 249-370. [ Links ]
Feynman, R., 1989. O que É uma Lei Física? Gradiva, Lisboa.
Goodman, D., 1993. The Demography of Chance Extinction. Em M. E. Soulé Viable Populations for Conservation, Cambridge University Press, Cambridge, pp. 11-34.
Kimmel, M., Axelrod, D.E., 2002. Branching Processes in Biology. Springer, New York.
Lande, R., Engen, S., Sæther, B-E., 2003. Stochastic Population Dynamics in Ecology and Conservation. Oxford University Press, Oxford.
Morris, W.F., Doak, D.F., 2002. Quantitative Conservation Biology. Theory and Practice of Population Viability Analysis. Sinauer Associates, Inc. Publishers, Sunderland, MA.
Entregue para publicação em Outubro de 2007
Aceite para publicação em Fevereiro de 2008